基于Arnold变换的高效率分块图像置乱算法的研究

王圆妹，李 涛

(长江大学电子信息学院，湖北 荆州 434023)

互联网技术的飞速发展，为信息在网上的快速传播开辟了新道路。利用互联网可以使信息迅速地在网上发布和传输，但同时也给不法分子利用网络非法获取未授权数据提供了渠道，因此信息安全已成当前学术研究的热点。当前对图像信息的保护主要有数字水印和图像加密两种方法。图像置乱［1］是一种重要的图像加密方法，也是信息隐藏［2］的基础，可进一步作为数字图像隐藏、数字水印植入、数字计算恢复方法和数字图像分存的预处理和后续处理过程。数字图像置乱加密是一种重要的数据加密技术，并可作为有效的安全增强手段。

常见的图像置乱算法主要有基于Arnold变换、Fibonacci变换、Hilbert变换、幻方变换等，主要通过改变像素点位置和改变像素点灰度值这两种方法达到置乱的效果。改变像素点位置的方法一般用于矩阵变换，通过消除像素点间的相似性和相关性来改变像素点的位置。由于Arnold变换具有一定的混沌性，把它用到图像加密处理可以获得较好的置乱效果。但由于Arnold变换的周期性和参数较少的原因，在数据加密时容易受到外部的攻击和破坏。Kwok H S等人［3］从位置变化的角度进行分析，若计算图像置乱前后的位置移动的距离，位置移动的距离越大，置乱效果越好。本文在Arnold变换基础上提出一种高效率的基于分块的图像置乱算法，并通过大量的实验验证了此方法的有效性。该方法置乱速度快，迭代次数少，执行效率高，置乱效果好，提高了保密信息的安全性。

1 二维Arnold变换

一幅大小为N×N的图像经过数字化处理后的得到的是一个二维离散的数字矩阵，矩阵中每个元素代表图像信息，(x，y)为原始的像素坐标，(x'，y')表示变换之后的像素位置，并且 (x，y)∈ (0，1，…，N － 1);mod 表示求余运算，目的是保证图像的数据阵进行变换后仍然落在在原先的图像区域内，因此二维的Arnold变换［4－5］可表示为当a=1，b=1时则为标准的Arnold变换，公式为

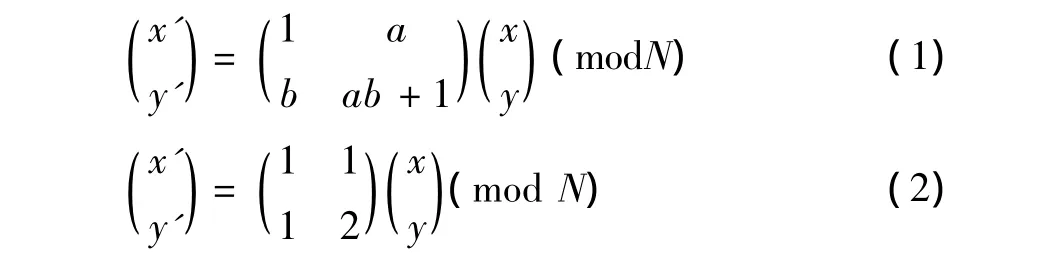
一幅图像经过Arnold变换后，图像像素点的位置在空域进行重新排列，通过改变像素点坐标而改变图像灰度值的分布，这样图像像素点的分布变的杂乱无序，实现了对图像进行置乱加密。图像通过Arnold变换虽然可以使图像变得混乱，但是这种混乱程度是有限度的，并不是随着迭代次数增多，置乱图像就越来越“乱”，往往存在最佳的迭代次数，置乱程度最好，置乱效果最佳。置乱次数与置乱程度的关系如图1 所示［6－9］。

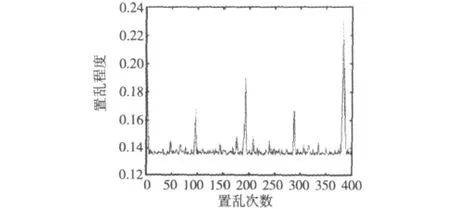
图1 置乱次数和置乱程度的关系

由于 Arnold 变换具有周期性［10－11］，即当迭代次数达到一定值后，所有像素点又都回到初始位置，存在等式(xn，yn)=(x0，y0)，置乱图像和原始图像一模一样。可以利用这一特性将置乱图像还原为原始图像，具体实现方法为:发送方将变换周期L和传输图像的置乱次数n作为密钥包含的内容，接收方利用Arnold变换具有周期性的特点，对传输图像再作L－n次置乱，即可得到原始图像。恢复的具体过程如图2所示。

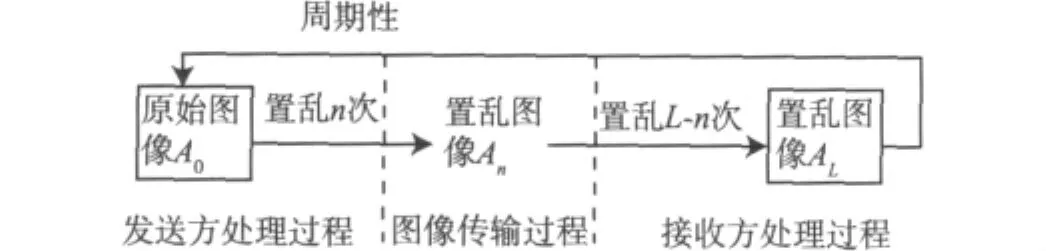
图2 利用周期性还原图像

2 高效率的分块图像置乱算法

上述基于Arnold变换的置乱算法虽然计算简单，很容易实现，也有较好的置乱效果，但是当图片较大时，Arnold变换的周期很大，如果利用周期性恢复原图像，往往需要很长时间，这样恢复的效率将迅速降低。文中提出的基于Arnold变换的分块图像置乱算法，缩短了置乱变换的周期，提高了算法的执行效率。

假设一幅图像的大小为N×N(N＞32时)，置乱周期都比较大。这时可以将N×N大小的图像划分成若干个大小为a×a的图像块，共有

图像块;然后对每个图像块中的像素点进行置乱，相应得到混乱状态的图像块，再对这些图像块进行置乱，不断打乱图像块的排列顺序，最后完成了整幅图像的置乱，其过程如图3所示。

对高效率的分块置乱算法仍然可以借用基于Arnold变换置乱算法的周期性恢复方法进行对图像的恢复。若L1表示图像块进行Arnold变换的置乱周期，L2表示图像块内像素点进行Arnold变换的置乱周期。假设图像块的进行Arnold变换次数为p，图像块内像素点的进行Arnold变换迭数为q，则只需要再对图像块作L1－p次Arnold变换，对图像块内像素点作L2－q次Arnold变换，就可以恢复出整幅图像了。

图3 高效率分块置乱算法流程图

3 仿真实验结果与分析

3.1 算法的实现及恢复

对一幅256×256的图像，采用不同的分块方法得到的置乱效果如图4所示。

图4 不同分块方法的置乱结果

利用本文算法的周期性，只需改变2次Arnold变换的迭代次数就可以使置乱图像还原，其结果如图5所示。

图5 置乱图像的恢复

从置乱结果可以看出，图像块越小，置乱图像的灰度值分布越均匀。由于图像块具有“聚合”的特点，它会使像素点集中在一起，影响置乱的均匀度。利用此算法时还有一个关键问题是要选取合适的图像块数，即如何对图像进行分块。在上述实验中对一幅大小为256×256的图像，其置乱周期为192，完成这一周期，每个像素点都要移动192次，共需要移动256×256×192次。若采用本文提出的置乱算法，把256×256图片分为32×32块，每块有8×8个像素点，完成这一周期，每个块要移动30次，因此，利用本文置乱算法完成对图像置乱，所有像素点的总移动次数是256×256×30次，仅是原来置乱算法的15/96，计算效率提高将近85%。

3.2 抗攻击性能分析

图像置乱的目的是为了图像得到安全加密，不仅要阻止攻击者恢复原图像，窃取图像信息，还要阻止攻击者对图像破环，文中主要从抗剪切及噪声等方面对置乱算法的抗攻击性进行分析。

1)抗剪切攻击能力

利用本文提出高效的分块图像置乱方法对图像进行剪切再恢复，其结果如图6所示。

图6 分块图像置乱算法的抗剪切能力

从上述图像可以看出，恢复图像的清晰度与剪切的大小有关，与剪切的位置无关。当攻击者剪切部分面积越大，图像越不清晰，甚至会导致图像信息完全被破坏，接收方得不到完整的图像信息。由于图像块的“聚合”特性，利用本文的算法对遭到剪切攻击后的置乱图像进行恢复图像，恢复出的图像还存在着一些噪声，为此抗剪切的能力还有待进一步提高。

2)抗噪声攻击能力

图片在实际传输过程中，往往会有各种噪声干扰，信道的传输环境不可能完全呈现理想状态。实验中对置乱后图像加不同类型的噪声，然后用逆变换方法还原加噪的置乱图像，得到相应的结果如图7所示。

图7 对置乱图像加不同噪声及恢复

从图7可以，看出置乱图像加噪声后恢复出的图像都比较清晰。还可以采用一种评价图像的客观标准峰值信噪比(PSNR)来衡量图像质量，分别计算恢复图像和原始图像的PSNR，具体如表1所示。

表1 恢复图像与原始图像的PSNR

从图4～图7的视觉效果及表1的数据可看出，计算出的PSNR值都比较大，这表明文中基于分块的置乱算法具有很好的抗噪性能力。

4 结论

本文提出了一种高效率的分块的图像置乱方法。与常用的基于Arnold变换的置乱算法相比，该算法具有计算量小、运行速度快、效率高等优点。由于图像块具有聚合的特点，本文的算法在对抗剪切能力分析时，还原的图像还具有一定的噪声。因此，在提高效率的同时如何增强本算法的稳健性是下一步重点研究内容之一。

［1］顾成喜.一种改进的数字图像置乱方法［J］.计算机仿真，2011，28(1):261－264.

［2］郎永祥，秦拯.应用于实时通信版权保护的BTC图像水印技术［J］.电视技术，2011，35(17):12－14.

［3］KWOK H S，TANG W K S.A fast image encryption system based on chaotic maps with finite precision representation［J］.Chaos，Solitons＆ Fractals，2007，32(4):1518－1529.

［4］KINGSTON A，SVALBE I.Generalised finite radon transform for N ×N images［J］.Image and Vision Computing，2007，25(10):1620－1630.

［5］陈善学，姚小凤，周淑贤.一种Arnold变换的改进方法［J］.电视技术，2011，35(17):33－35.

［6］邱炳城，姚仰新，陈银冬.用小波变换和混沌映射实现图像置乱［J］.计算机工程与应用，2009，45(11):102－103.

［7］邓绍江，张岱固，濮忠良.一种基于混沌的图像置乱算法［J］.计算机科学，2008，35(8):238－240.

［8］陈燕梅，张胜元.基于交叉熵的数字图像置乱程度评价方法［J］.中国图象图形学报，2007，12(6):997－1001.

［9］王远志，张歌凌，张健，等.分布均匀性的图像置乱衡量方法［J］.计算机工程与应用，2009，45(34):156－158.

［10］KWOK H S，TANG W K S.A fast image encryption system based on chaotic maps with finite precision represention［J］.Chaos，Solitons ＆Fractals，2007，32(4):1518－1529.

［11］HUN Chenhe.Parallel image encryption algorithm based on discrete chaotic map［J］.Chaos，Solitions ＆ Fractals，2007，54(3):158－159.