一类灰色问题性质研究

吴正朋，张友萍，尧欣怡，李梅

(1.中国传媒大学应用数学系，北京 100024;2.北京第二外国语学院继续教育学院，北京 100024)

一类灰色问题性质研究

吴正朋1，张友萍1，尧欣怡2，李梅1

(1.中国传媒大学应用数学系，北京 100024;2.北京第二外国语学院继续教育学院，北京 100024)

在灰色系统缓冲算子公理体系下，本文证明了下列结果:若d是一强化缓冲算子，x(k)d由x(k)，…，x(n)所构成的表达式，f为严格单调递增函数，g为f的反函数。在x(k)d中，将f(x(k))替换x(k)(k=1，…，n)，对得到的新表达式，用函数g去作用，最后的表达式记为e，若d为强化缓冲算子，则e也为强化缓冲算子.

强化缓冲算子;灰色系统

1 引言

灰色系统的特色是研究“小样本”与“贫信息”等不确定性问题。因此充分开发利用已占有的信息来挖掘系统本身固有的规律是灰色系统理论的基本准则。我们可以通过社会、经济、生态等系统的行为特征数据来寻求因素之间或自身的变化规律。灰色系统理论认为，尽管客观系统的表象复杂，数据离乱，但它们总有自身的整体功能，必然蕴藏某种内在的规律。关键是如何选择适当的方法来挖掘和利用它。在文献［1，4，5，7］中，刘思峰等教授提出了冲击扰动缓冲算子的概念，并构造出一种得到较广泛应用的强化缓冲算子。本文在他们的工作的基础上，又构造出一新强化缓冲算子，从而推广了缓冲算子的类型。

2 基本概念

定义2.2设X为系统行为数据序列，D为作用于X的算子，X经算子D作用后所得到序列记为XD=(x(1)d，x(2)d，…，x(n)d)，则称 D 为序列算子。

对序列连续作用，可得二阶算子，一直可以作用到 r阶算子，分别记为 XD2，…，XDr。

公理2.1［4］(不动点公理)设X为系统行为数据序列，D为序列算子，则有x(n)d=x(n)。

公理2.2［4］(信息充分利用公理)系统行为数据序列X中的每一个数据x(k)(k=1，2，…，n)，都应充分地参与算子作用的整个过程。

公理2.3［4］(解析化与规范化公理)任意的 x(k)d(k=1，2，…，n)皆可以由一个统一的 x(1)，x(2)，…，x(n)的初等表达式表达。

满足上述三公理的序列算子称为缓冲算子。XD称为缓冲序列。

定义2.3［5］设X为系统行为数据序列，D为序列算子，当X为单调增长序列、单调衰减序列或振荡序列，缓冲序列XD比行为数据序列X的增长速度(或衰减速度)增强或振幅增大，则称缓冲算子D为强化算子。

定理 1［5］

(1)设X为单调增长序列，XD为缓冲序列，则

由定理1可知，单调增长序列在强化缓冲算子作用下，数据萎缩;单调衰减序列在弱化缓冲算子作用下，数据膨胀。

3 一类新的强化缓冲算子的构造

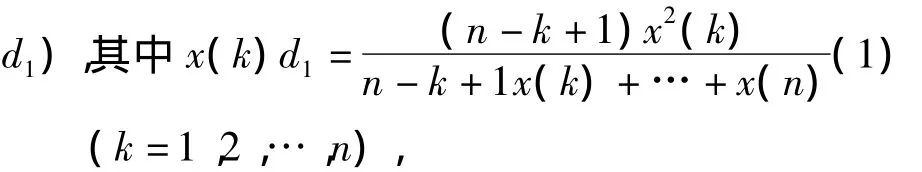
则当X为单调增长序列、单调衰减序列或振荡序列时，D1皆为强化缓冲算子。

在此，我们在强化缓冲算子D1基础上，证明下列新结果。

定理2设X=(x(1)，x(2)，…，x(n))为非负的系统行为数据序列，且x(i)＞0，f＞0，f为严格单调递增函数，g为其反函数。若d是强化缓冲算子，x(k)d由x(k)，…x(n)所组成，在d中，用 f(x(k))替换x(k)，(k=1，…，n)，对所得到的表达式用函数 g去作用，则新表达式e也为强化缓冲算子。

证明:因为d为强化缓冲算子，则x(n)d=x(n)，

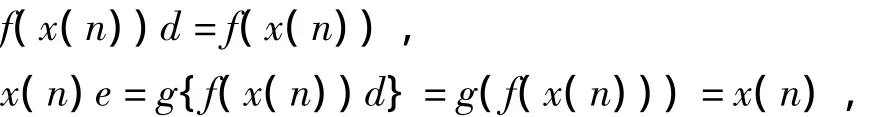
即e满足缓冲算子公理一。

至于缓冲算子公理二，公理三显然成立，因而e为缓冲算子。

假设f为严格单调递增函数，

下证当:

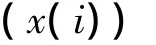
因为d为强化缓冲算子，则

所以e为强化缓冲算子。

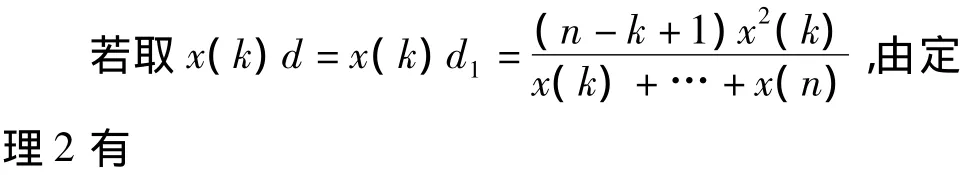
推论1 设X=(x(1)，x(2)，…，x(n))为非负的系统数据序列，且x(i)＞0，f＞0，f为严格单调递增函数，g为其反函数，

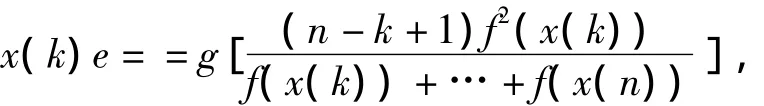
则e也是强化缓冲算子。

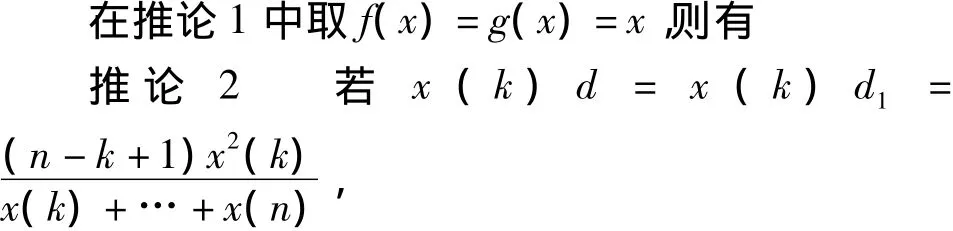
则d1也是强化缓冲算子。

4 结语

在缓冲算子的构造过程中，若d是由x(1)，…，x(k)，…，x(n)所构成的强化缓冲算子，则由上述方式所生成的表达式e也是强化缓冲算子。

［1］刘思峰，党耀国，方志耕.灰色系统理论及其应用［M］.北京:科学出版社，2004.

［2］Liu Si-feng.The three axioms of buffer operator and their applications［J］.The Journal of Grey System，1991，3(1):39—48.

［3］刘思峰.缓冲算子及其应用［J］.灰色系统理论与实践，1992，2(1):45—50.

［4］刘思峰.冲击扰动系统预测陷阱与缓冲算子［J］.华中理工大学学报，1997，25(1):25—27.

［5］谢乃明，刘思峰.一种新的弱化缓冲算子［J］.中国管理科学，2003，11(增):46—48.

［6］党耀国，刘思峰，刘斌.关于弱化缓冲算子的研究［J］.中国管理科学，2004，12(2):108—111.

［7］党耀国，刘斌，关叶青.关于强化缓冲算子的研究［J］.控制与决策，2005，20(12):1332—1336.

A Note on the Buffer Operator

WU Zheng-peng1，ZHANG You-ping1，RAO Xin-yi2，LI Mei1

(1.Department of Applied Mathematics，Communication University of China，Beijing 100024;2.School of Continuing Education，Beijing International Studies University，Beijing 100024)

Based on the present theories of buffer operators，we prove the following conclusion:f is a strict monotonic function，and g is its inverse function.If x(k)d is a strengthening buffer operator，then g(f(x(k)d)is also a strengthening buffer operator.

strengthening buffer operator;grey system

N941.5

A

1673-4793(2012)01-0024-03

2011-10-10

吴正朋(1964-)，男，中国传媒大学理学院副教授.E-mail:wuzhengpeng@126.com

(责任编辑

:宋金宝)