调整步长牛顿法
刘停战,刘伟,何颖
(中国传媒大学 理学院,北京 100024)
调整步长牛顿法
刘停战,刘伟,何颖
(中国传媒大学 理学院,北京 100024)
本文研究了求解非线性方程组的迭代解法,提出了一种调整步长牛顿法。证明了该算法在不同条件下的二阶收敛性和大范围收敛性。
非线性方程组;牛顿法;调整步长牛顿法
1 引言
设F是实的或复的高维Banach空间上的某个凸子集Ω到同型空间S上的非线性算子,考虑求方程组

的解,其中F(x)=(f1(x),…,fn(x))。我们知道在迭代法中,牛顿法和牛顿下山法最具代表性,牛顿法有二阶收敛性,牛顿下山法有大范围收敛性。牛顿法和牛顿下山法的迭代格式分别为:
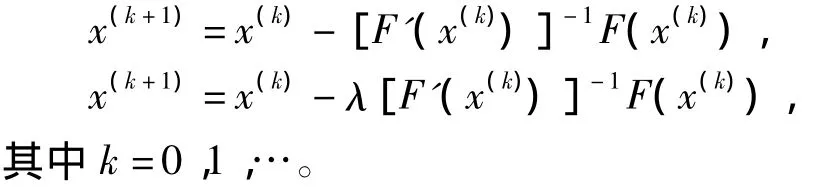
2 调整步长牛顿法
我们构造方程组(1)的等价方程组

对(2)式使用牛顿法,得到牛顿迭代格式:

注 该算法是牛顿下山法的推广。当0<λ1=λ2=…=λn≤1时,调整步长牛顿法就简化为牛顿下山法。当λ1=λ2=…=λn=1时,调整步长牛顿法即为牛顿法。
3 调整步长牛顿法的收敛性
关于调整步长牛顿法的收敛性及收敛阶,我们有:

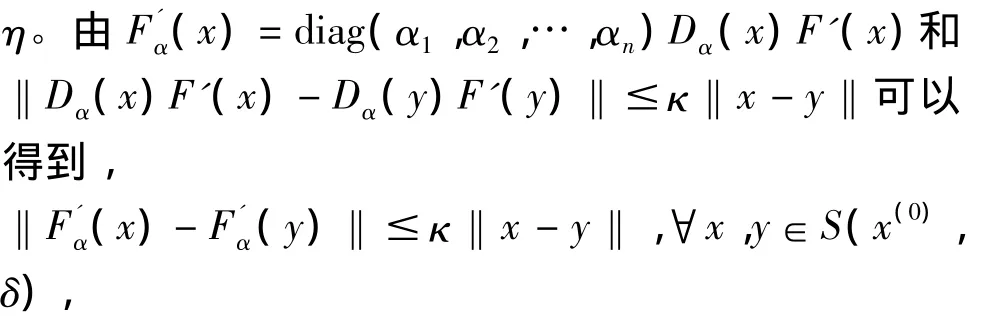
由以上可知,满足Kantorovich定理的条件,所以结论成立。
定理1 给出了调整步长牛顿法的半局部收敛性,下面讨论调整步长牛顿法的大范围收敛性。


于是利用上式立即导出x(k)有极限x*∈Ω0存在,并注意‖[F'(x(k))]-1‖≤β以及λk的有界性。对(7)式令k→∞导出F(x*)=0。这样就证明了调整步长牛顿法的大范围收敛性。
4 数值实验
本节将考虑使用上述调整步长牛顿法与牛顿法来计算一个例子,迭代终止条件为‖xk-x(k-1)‖<10-6。
例1

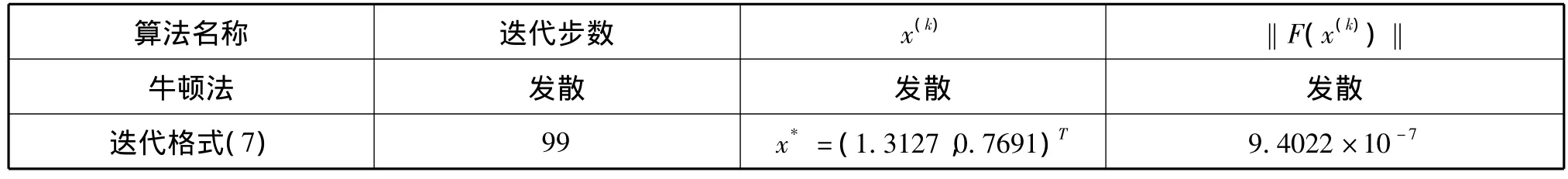
表1
通过表l的计算结果可以看出当初始迭代点x(0)距离解较远时,牛顿法发散,调整步长牛顿法却收敛,这就说明了迭代格式(7)具有大范围收敛性。
[1]刘兴龙.解非线性方程组的一种带参数的Newton方法[J].哈尔滨工业大学学报,1979(2):97-104.
[2]冯果忱.非线性方程组迭代解法[M].上海:上海科学技术出版社,1989.
[3]卢兴江.关于解非线性方程组的Newton型迭代法的若干研究[J].浙江丝绸工学院学报,1998,15(2):141-144.
[4]Ortega JM,RheinboldtW C.多元非线性方程组迭代解法[M].北京:科学出版社,1983.
Step-adjusting New ton M ethod
LIU Ting-zhan,LIUWei,HE Ying
(School of Science,Communication University of China,Beijing 100024,China)
In this paper,we studied iterative method for solving nonlinear equations and obtained stepadjusting Newton method.Second-order convergence and global convergence are also proved in different conditions.
nonlinear equations;Newton method;step-adjusting Newton method
O241.7
A
1673-4793(2012)01-0008-03
2011-07-12
刘停战(1954-),男(汉族),吉林长春人,中国传媒大学理学院教授.E-mail:tzliu@cuc.edu.cn.
(责任编辑
:宋金宝)

