基于预测码辅助的CDMA系统盲NBI抑制技术
殷复莲
(中国传媒大学信息工程学院,北京 100024)
基于预测码辅助的CDMA系统盲NBI抑制技术
殷复莲
(中国传媒大学信息工程学院,北京 100024)
在信号统计特性和训练序列未知的情况下,针对现存盲自适应最小均方(LMS,Least Mean Square)码辅助算法码分多址(CDMA,Code Division Multiple Access)系统强窄带干扰(NBI)进行抑制时稳态性能较差,以及盲自适应递归最小二乘(RLS,Recursive Least Square)码辅助算法收敛速度和性能难以折中的问题,提出盲自适应预测码辅助技术。盲自适应预测码辅助技术基于盲自适应RLS预测-LMS码辅助算法实现,实现了对三类NBI的抑制,包括音频干扰、数字窄带干扰和自回归(AR,Autoregressive)随机过程。本文详细分析了盲自适应RLS预测-LMS码辅助算法的性能,并通过仿真分析证明了算法的有效性。
码分多址系统;窄带干扰抑制;盲自适应预测码辅助技术;RLS算法;LMS算法
1 引言
现存的直接码分多址(CDMA,Code Division Multiple Access)系统窄带干扰(NBI,Narrow-Band Interference)抑制技术主要包括预测技术、变换域技术和码辅助技术三大类。预测技术是最早出现的NBI抑制技术之一,CDMA系统的NBI抑制技术包括线性预测技术、判决反馈技术和非线性预测技术3大类[1-2]。变换域技术是另一最早出现的NBI抑制技术之一,应用的变换域包括频域、小波域、时频域和空时域[3-4]。预测技术和变换域技术均采取了先抑制NBI,后对抗多址干扰(MAI,Multiple Access Interference)的方式,无法联合抑制NBI和MAI。码辅助技术利用信号码特征进行块处理,将NBI分解成互不重叠的虚拟用户,则由一个实际CDMA系统和m个虚拟用户构成了一个新的虚拟CDMA系统。利用多用户检测技术的思想,将虚拟用户作为MAI处理,可达到NBI和MAI的联合抑制效果,是该领域最有前途的技术之一[5-6]。
CDMA系统常见的NBI主要包括音频、数字NBI和自回归(AR,Autoregressive)随机过程。在信号统计特性和训练序列未知的情况下,盲自适应码辅助干扰抑制技术引起越来越多的重视[7-8]。目前研究比较广泛的盲自适应码辅助算法包括LMS算法和RLS算法[9-10]。为了解决盲自适应LMS码辅助算法稳态性能较差和盲自适应RLS码辅助算法收敛速度与性能难以折中的问题,本文提出盲自适应预测码辅助算法,基于忙自适应RLS预测-LMS码辅助算法实现。
2 信号预处理
2.1 离散化信号模型
离散采样是干扰抑制的重要环节,切普匹配滤波获取的离散采样序列r(m)可以表示为

式中y(m)为CDMA采样信号;i(m)为NBI采样信号;ε(m)为功率谱密度为的高斯白噪声采样信号。
CDMA采样信号可以建模为

式中Kz(Kz≥1)为MAI用户数目;Ak为第k个用户接收信号幅度;bk(n)为第k个用户信号流(1或-1),b0(n)为期望用户信号流;sk为第k个用户直接序列扩频码采样值。
现存的NBI主要包括音频干扰、数字窄带干扰和AR随机过程三大类。音频干扰离散模型为:

式中Ki为音频干扰数目为音频干扰归一化幅度为音频干扰归一化频率且只考虑为整数;N为扩频增益。
数字NBI采样信号可以建模为
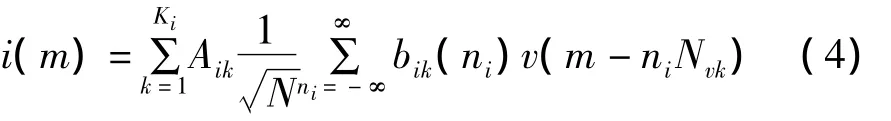
式中Ki为音频干扰数目;Aik为第k个数字窄带干扰接收信号幅度;bik(n)为第k个数字NBI信号流(1或-1),持续时间Tik>>Tc且只考虑Nvk=Tb/Tik为整数的情况;v(·)为单位高度矩形脉冲。
AR随机过程采样信号可以建模为
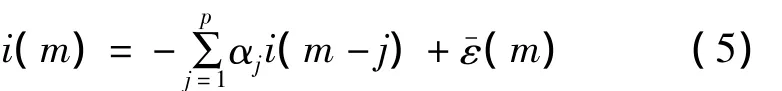
式中p为AR随机过程阶数;ε-(m)为功率谱密度的高斯白噪声序列。
2.2 信号加窗模型
码辅助技术对接收信号进行块处理,对于第n个发送信号,在处理间隔[nTb,(n+1)Tb]内对采样信号r(m)加窗得到(N×1)维加窗向量r(n)=[r(nN+N-1),r(nN+N-2),…,r(nN)]T。

式中:y(n)、i(n)和 ε(n)分别为 CDMA、NBI和高斯白噪声加窗信号。
2.3 信号二阶统计特性
自相关矩阵反映了信号的二阶统计特性,加窗信号r(n)的自相关矩阵Rrr(n)定义为

式中:Ryy(n)E{y(n)yT(n)}为CDMA加窗信号自相关矩阵;Rii(n)=E{i(n)iT(n)}为NBI加窗信号自相关矩阵;Rεε(n)=E{ε(n)εT(n)}为高斯白噪声加窗自相关矩阵。
3 现存盲自适应码辅助技术
3.1 盲自适应LMS码辅助算法
LMS算法和RLS算法是现在盲自适应码辅助领域最常见的两类算法,盲自适应LMS算法的实现基于最小输出能量(MMOE,Minimum Mean Output Energy)准则。
表1给出了盲自适应LMS码辅助算法流程。表中定义滤波向量wBLMS;投影梯度矩阵P=IN-s0;步长因子μBLMS;抽头平均输入功率为Pin。

表1 盲自适应LMS码辅助算法
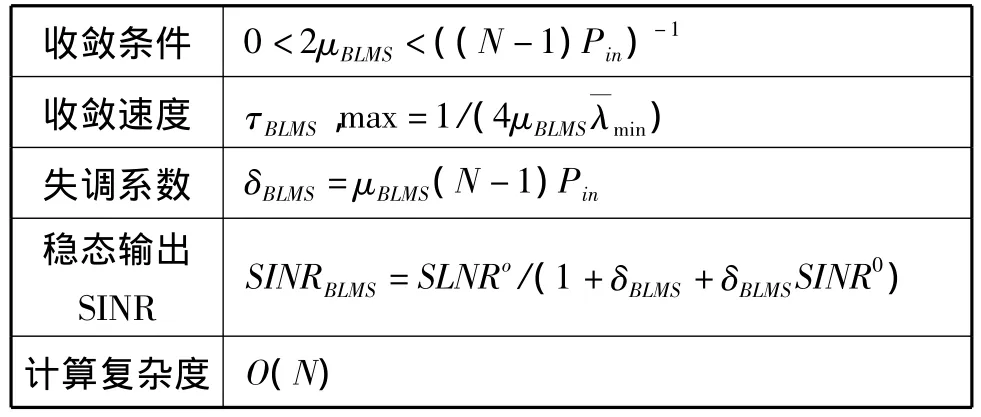
表2 盲自适应LMS码辅助算法性能归纳
如表所示,本文研究的强NBI环境由于抽头平均输入功率过高导致失调系数很大,这使得算法的稳态输出SINR上限1/δBLMS严重受限而影响算法性能。在这种情况下,可以通过降低步长因子的方法改善系统性能,但强抽头平均输入功率导致的特征值分散已经使算法收敛速度很慢,进一步降低步长因子更将影响收敛速度。可以说,在强NBI环境,算法稳态输出SINR性能受限是盲自适应LMS码辅助算法的最大缺陷。
3.2 盲自适应RLS码辅助算法
在码辅助领域,直接法盲自适应RLS码辅助算法基于MMOE准则实现。
设定盲自适应RLS码辅助算法相关逆阵CBCA∈RN×N、递归向量 kBCA∈RN×1和遗忘因子 0 < λBCA<1。表3给出了盲自适应RLS算法流程,对输入数据、参数设计和初始化条件进行了描述。
表4给出了盲自适应RLS码辅助算法性能归纳。

表3 盲自适应RLS码辅助算法

表4 盲自适应RLS码辅助算法性能归纳
如表所示,盲自适应RLS码辅助算法的收敛速度与受失调系数控制的稳态输出SINR是一个矛盾体。收敛速度要求遗忘因子越小越好,而失调系数要求遗忘因子越大越好。也就是说,盲自适应RLS码辅助算法的缺陷是系统稳态输出SINR性能的提高必将导致收敛速度的下降,系统收敛速度的提高也必将导致系统稳态输出SINR的降低,二者不可折中。此外,盲自适应RLS算法存在的另一缺陷是系统复杂度较高。
4 优化盲自适应预测码辅助技术
4.1 预测模块对NBI功率的衰减作用
强NBI环境产生抽头输入功率过高,盲自适应LMS码辅助算法由于收敛因子需要满足收敛速度要求而产生的最大问题是稳态性能较差;盲自适应RLS码辅助算法存在的最大问题是收敛速度和系统稳态性能之间的不可折中,以及高系统复杂度。如果能够找到一种在进行盲自适应LMS码辅助算法前有效降低NBI功率的方法,无疑是最好的解决方案。
预测码辅助技术,即在执行码辅助滤波前,首先利用预测滤波做预处理,可以较好的解决以上问题。表5给出了最优线性预测滤波情况下预测模块对各类NBI功率的衰减作用。
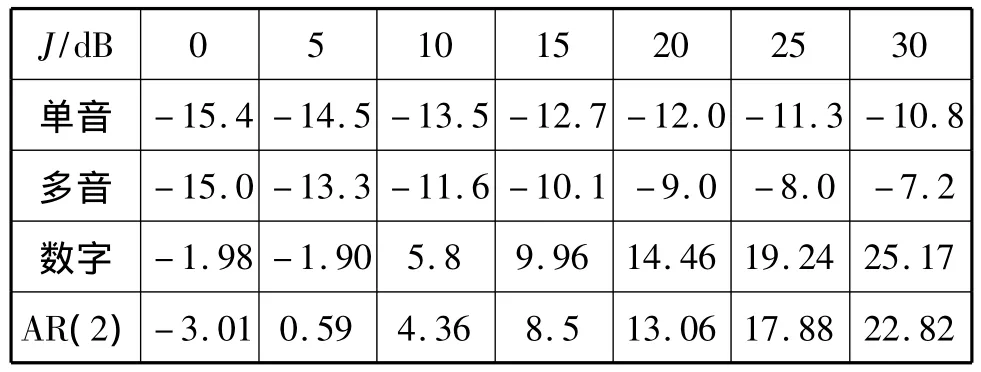
表5 预测模块对各类NBI功率的衰减作用
如表所示,在音频干扰总功率相等的情况下,单音干扰功率的降低幅度大于多音干扰功率的降低幅度。对于数字NBI,表中设定Nv=4,如表所示,由于数字NBI符号边缘存在跳跃,使得LP模块对数字NBI的抑制效果明显弱于对音频干扰的抑制效果。对于二阶AR随机过程AR(2),设定α1=-0.9、α2=0.81,AR(2)对应结论与其他阶AR随机过程完全相同,这里不再赘述。综上所述,对于各类NBI,线性预测输出功率的降低幅度都非常明显。
4.2 盲RLS预测-LMS码辅助算法
在线性预测领域,比较成熟的算法包括LMS和RLS预测算法。如果选取LMS预测算法,将存在特征值扩散的问题;而RLS预测算法由于失调系数和收敛速度不受自相关矩阵特征值影响,无疑是最好的选择。因此,本文构造盲自适应RLS预测-LMS码辅助算法作为改进算法。
改进的的盲自适应RLS预测-LMS码辅助算法的优越性能通过如下过程分析。首先观察表2的失调系数,降低抽头平均输入功率可以有效减小失调系数,进而提高表2的稳态输出SINR上界1/δBLMS。抽头平均输入功率的降低还使盲自适应LMS码辅助算法的特征值扩散问题得以解决,改进算法能够以较快的收敛速度达到较高的性能,较盲自适应RLS码辅助算法具有明显优势。最后,改进算法的计算复杂度略高于盲自适应LMS码辅助算法,明显低于盲自适应RLS码辅助算法,是可以接受的。
盲自适应RLS预测-LMS码辅助算法由盲自适应RLS预测滤波和盲自适应LMS码辅助滤波组成。表6给出了盲自适应RLS预测-LMS码辅助算法流程。其中设定步长因子μRLS-BLMS和预测后的抽头平均输入功率。
(1)盲自适应RLS预测算法
盲自适应RLS预测算法采用经典算法。
(2)盲自适应LMS码辅助算法
盲自适应RLS预测滤波后的盲自适应LMS码辅助算法递归表达式与盲自适应LMS码辅助算法形式相同,仅输入信号不同
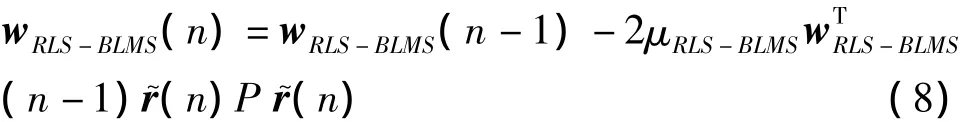
考虑到接收信号非理想自相关特性,对投影梯度矩阵进行修正
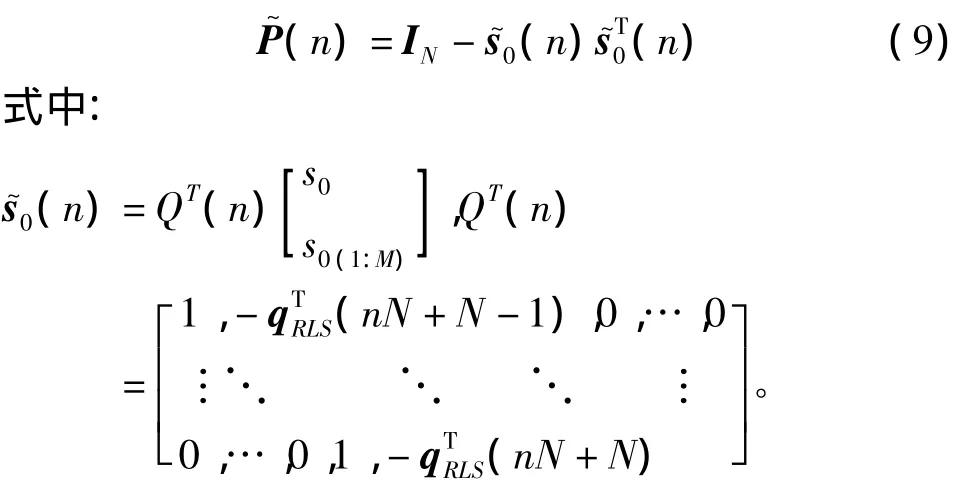
进而得到盲自适应RLS预测-RLS码辅助递归表达式


表6 盲自适应RLS预测-LMS码辅助算法

续表
4.3 盲RLS预测-LMS码辅助算法性能分析
以下分别从收敛条件、收敛速度、失调系数、输出SINR和计算复杂度的角度分析盲自适应RLS预测-LMS码辅助算法性能。
(1)收敛条件
盲自适应RLS预测算法的数值稳定条件和盲自适应LMS码辅助算法的收敛条件分别为

(2)收敛速度
在盲自适应RLS预测-LMS码辅助算法中,收敛速度主要由加窗信号数量级的盲LMS码辅助算法决定,而近似忽略采样信号数量级的盲RLS预测算法。盲自适应RLS预测-LMS码辅助算法的最大时间常数为
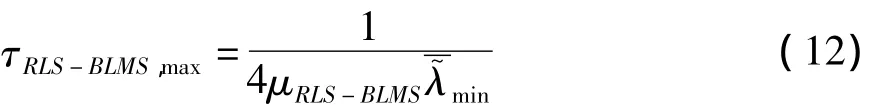
(3)失调系数
盲自适应RLS预测算法失调系数在λLP=1时为0可忽略,即盲自适应RLS预测-LMS码辅助算法的失调系数由盲自适应LMS码辅助算法决定,表示为

由于经过预测滤波后的输入功率大大降低,因而盲自适应RLS预测-LMS码辅助算法的失调系数将小于盲自适应LMS码辅助算法。
(4)稳态输出SINR
与盲自适应LMS码辅助算法类似,盲自适应RLS预测-LMS码辅助算法的系统输出SINR为

由于盲自适应RLS预测-LMS码辅助算法的失调系数较盲自适应LMS码辅助算法显著下降,故其稳态性能将显著提高。
(5)计算复杂度
盲自适应RLS预测-LMS码辅助算法的计算复杂度为RLS算法和LMS算法的总和N·O(M2)+O(N)。
表7给出了改进的盲自适应RLS预测-LMS码辅助算法性能归纳。

表7 盲自适应RLS-LMS算法性能归纳
横向观察表2、表4和表7。与盲自适应LMS码辅助算法相比较,盲自适应RLS预测-LMS码辅助算法的RLS预测模块对NBI进行滤波,从而大大降低了抽头平均功率(<<Pin)。抽头平均功率的降低减小了失调系数,提升了稳态输出SINR上限,改善了系统性能。
与盲自适应RLS码辅助算法相比较,抽头平均功率的降低解决了特征值扩散问题,使盲自适应RLS预测-LMS码辅助算法以较快的收敛速度达到较高的性能,解决了盲自适应RLS码辅助算法收敛速度和稳态性能难以同时保证的问题。同时,改进的盲自适应RLS预测-LMS码辅助算法较盲自适应RLS拥有明显的低计算复杂度优势。
综合分析:改进的盲自适应RLS预测-LMS码辅助算法优势明显,在直接法盲自适应干扰抑制领域,可以同时满足稳态性能、收敛速度以及计算复杂度的要求,是一种最优选择。
5 仿真结果及分析
本节将对不同类型NBI情况的直接法盲自适应系统输出SINR进行仿真验证。图中““BLMS”表示盲自适应LMS码辅助算法;“RLS-BLMS”表示盲自适应RLS预测-LMS码辅助算法;盲自适应RLS码辅助算法通过标注遗忘因子λBCA表示。
盲自适应LMS码辅助算法收敛因子取满足收敛条件的最大值、改进的盲自适应RLS预测-LMS码辅助算法在不降低稳态性能的前提下较前者提高一个数量级左右,以上两种LMS类算法在一幅图中进行对比。而对于盲自适应RLS码辅助算法,由于遗忘因子同时控制稳态性能和收敛速度,故将遗忘因子变化情况下的仿真验证在另一幅图中给出,遗忘因子分别取0.9、0.99和0.999。同时,在分析过程中,将对二者进行横向比较。
实验1:音频干扰情况
图1给出了单音干扰情况的盲自适应算法输出SINR对比曲线(多音干扰情况结论与此相同),其中图(a)和(b)分别表示LMS类算法和RLS类算法。图中设定NBI功率J=30dB,预测滤波阶数M=6,高斯白噪声功率谱密度=0.01。
如图(a)所示,对于LMS类算法,盲自适应LMS码辅助算法稳态输出SINR性能较差,改进的盲自适应RLS预测-LMS码辅助算法稳态输出SINR性能得到了极大提高,同时通过选取合适的步长因子,可以在较快速度下达到稳态性能。如图(b)所示,对于RLS类算法,遗忘因子较小时,盲自适应RLS码辅助算法可以以较快速度收敛,但稳态输出SINR性能较差,当遗忘因子较大时,稳态输出SINR性能较好,却以收敛速度的极大下降为代价。横向比较图(a)和(b),盲自适应RLS预测-LMS码辅助算法从综合稳态性能和收敛速度的角度,较盲自适应RLS算法占据明显优势。
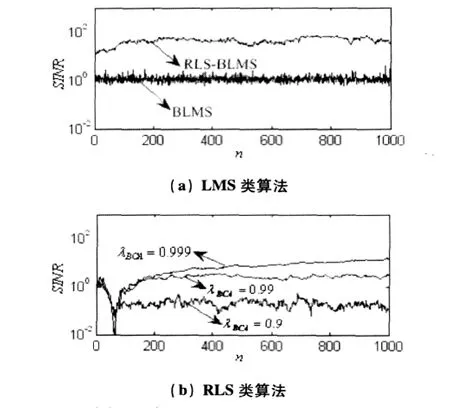
图1 音频干扰情况的盲自适应算法SINR对比曲线
实验2:数字窄带干扰情况
图2为数字NBI情况的盲自适应算法输出SINR对比曲线,其中图(a)和(b)分别表示LMS类算法和RLS类算法。中设定J=30dB,M=1,=0.01。

图2 数字窄带干扰情况的盲自适应算法SINR对比曲线
如图所示,可以得到与音频干扰情况相同的结论。特别的,由于数字NBI符号存在边缘跳跃使预测滤波受到限制,导致改进算法稳态性能的提高差于音频干扰情况。
实验3:AR随机过程情况
图3为AR随机过程情况的盲自适应算法输出SINR对比曲线。图中设定 M=2、J=15dB,=0.01。
如图所示,改进的盲自适应RLS预测-LMS码辅助算法稳态性能明显优于盲自适应LMS码辅助算法,且当综合考虑稳态性能和收敛速率时,横向优于盲自适应RLS码辅助算法。
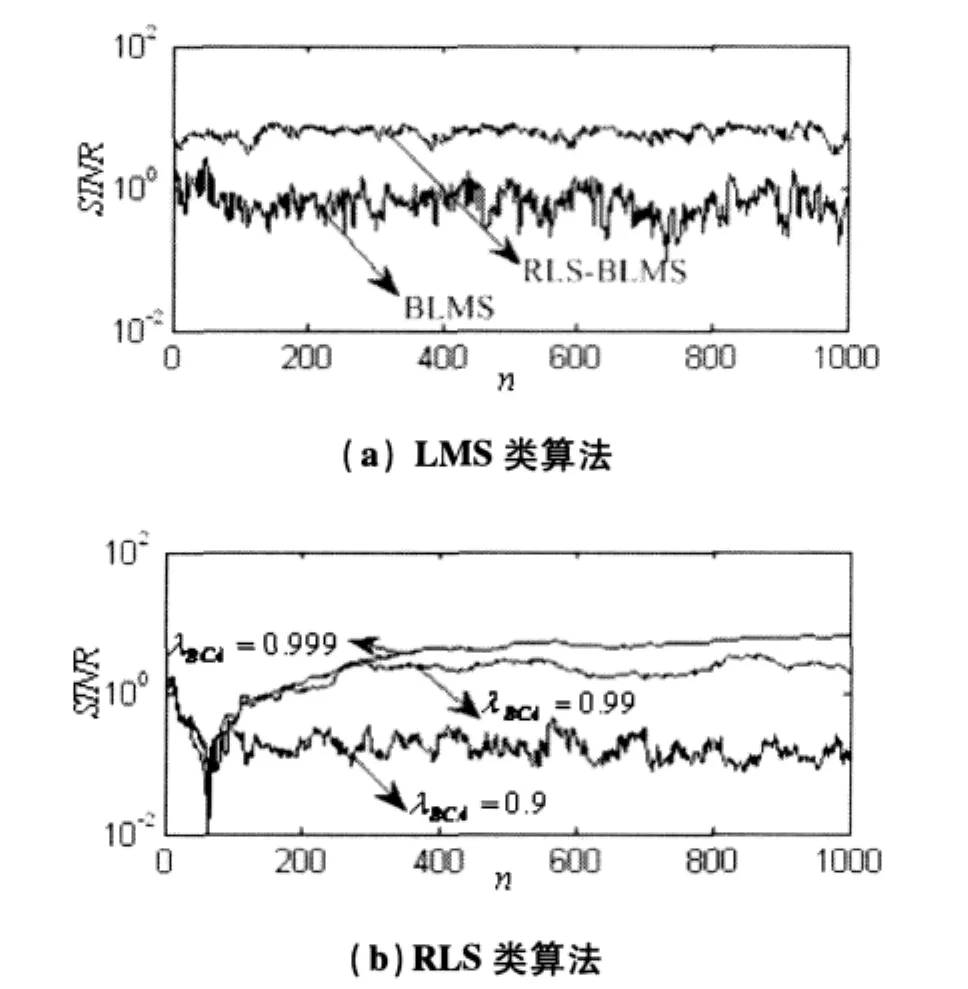
图3 AR随机过程情况的盲自适应算法SINR对比曲线
实验4:动态环境情况
在外界环境动态变化时,图4给出了改进的盲自适应RLS预测-BLMS码辅助算法输出SINR。仿真验证从单位信号能量的期望用户0、3个与期望用户等功率的MAI和J=30dB的单音干扰开始;n=1000时,3个MAI和单音干扰离开系统,J=30dB的数字NBI加入系统;n=2000时,数字NBI离开系统,3个与期望用户等功率的MAI和的AR(2)加入系统;n=3000时,3个MAI离开系统。以上音频干扰、数字NBI的参数设定同仿真 1;AR(2)的自回归系数设定 α1=-0.99、α2=0.9801,预测滤波阶数M=3。
如图所示,改进的盲自适应RLS预测-LMS码辅助算法能够快速跟踪环境变化,适合于移动环境中的实际应用。从图中还可以看到,存在MAI时,算法稳态性能产生波动。
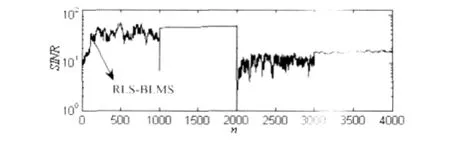
图4 动态环境盲自适应RLS-LMS算法SINR性能
6 信号预处理
本文为了解决现存盲自适应LMS码辅助算法稳态性能较差,盲自适应RLS码辅助算法收敛速度和性能难以折中的问题,提出盲自适应码辅助技术,基于盲自适应RLS预测-LMS码辅助算法实现。通过对盲自适应RLS预测-LMS码辅助算法性能的分析,得出其综合性能明显优于盲自适应LMS码辅助算法和盲自适应RLS码辅助算法的结论。仿真分析分别验证了对音频干扰、数字窄带干扰和AR随机过程进行抑制的算法有效性。
[1]黄高勇,张家树.一种抑制直扩通信窄带干扰的新型非线性自适应预测滤波器[J].电子与信息学报.2007,29(6):1328-1331.
[2]Z G SUN,L L GUO.An improved LSL interpolator to suppress narrow-band interference for direct-sequence spread-spectrum systems[J].1st International Conference on Communications and Networking in China,2007.
[3]M Y JIANG,D F YUAN,G P XU.Suppression of narrowband interference in DSSS systems based on CM MWPT and CWPT[J].IEEE International Symposium on Microwave,Antenna,Propagation and EMC Technologies for Wireless Communications,2005(1):1594-1597.
[4]孙永军,易克初.直接序列扩谱CDMA系统中盲窄带干扰抑制[J].系统仿真学报,2007,19(16):3756-3760.
[5]杨坚,奚宏生,吴春旭.基于自调整器的CDMA系统盲自适应干扰抑制[J].电子学报,2004,32(10):1617-1620.
[6]L L YANG,L C ZHANG.Zero-forcing and minimum mean-square error multiuser detection in generalized multicarrier DS-CDMA systems for radio[J].Eurasip J Wireless Commun Networking,2008(14):1-13.
[7]S BUZZI,M LOPS,H V POOR.Code-aided interference suppression for DS/CDMA overlay systems[J].IEEE Proceedings.2002(90):394-435.
[8]孙永军,易克初,孙恩昌.异步码分多址中盲窄带干扰抑制[J].系统工程与电子技术,2007,29(9):1410-1412.
[9]A ELNASHAR,S ELNOUBI,H EIMIKATI.Performance analysis of blind adaptive MOE multiuser receivers using inverse QRD-RLS algorithm[J].IEEE Signal Process,2008,55(1):398-411.
[10]J GOMES,V A N BARROSO.Array-based QR-RLS multichannel lattice filtering[J].IEEE Trans Signal Process,2008,56(81):3510-3522.
Blind Narrow-Band Interference Suppression based on Prediction and Code-aided for CDMA Sytems
YIN Fu-lian
(Information Engineering School,Communication University of China,Beijing 100024)
A blind adaptive prediction and code-aided technique for narrow-band interference(NBI)suppression of code division multiple access(CDMA)systems is proposed.This technique is based on blind adaptive recursive least square(RLS)prediction-least mean square(LMS)code-aided algorithm to solve the problem that adaptive LMS code-aided algorithm has poor steady state performance and adaptive RLS code-aided algorithm has conflict with constringency and steady performance.The rejection of this technique is against three type of NBI,namely,sinusoidal tones,data NBI and autoregressive(AR)stochastic process.In this paper,the performance of blind adaptive RLS prediction-LMS code-aided technique is analyzed.The feasibility of proposed algorithm is proved through simulations.
CDMA system;NBI Suppression;blind adaptive prediction and code-aided technique;RLS algorithm;LMS algorithm
TN911.72
A
1673-4793(2012)01-0037-08
2011-09-06
殷复莲(1982-),女(汉族),吉林蛟河人,中国传媒大学讲师.E-mail:yinfulian@cuc.edu.cn
(责任编辑
:宋金宝)

