基于后推技术的绳驱动拟人肩关节动力学控制

游贤强 陈伟海 崔 翔 于守谦

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

常规的串联结构的机器人将驱动电机安装于手臂上，增加了机器人的重量和转动惯量［1］，从而限制了机器人的承载能力，以及高速运动和快速响应能力.为了克服电机和连杆的重量所带来的不利影响，近年来绳驱动技术越来越引起人们的关注［2－3］.绳驱动3-3R球面并联机构利用绳索代替连杆来传递运动和力，具有结构简单、惯性小和运动速度快等优点［4－6］.将它作为拟人臂机器人的肩和腕关节，可将驱动电动机全部安放在机座，有效地减轻了手臂的自重，提高了快速响应能力［7］.

并联式绳驱动惯性小，精度高，在微操作方面很有应用优势，但并联式绳驱动建模困难、控制复杂，特别是由于外界扰动、载荷变化，系统参数难以正确估计和确定.这些问题导致绳驱动机器人在实际应用中是无法回避动力学和张力控制问题的，不能够像刚性机器人那样仅靠运动学控制就可以满足一般作业任务的要求.因此，动力学的研究对并联机器人高精度控制具有重要意义.

国内外对动力学的研究大多数都是针对传统的刚性机器人，以及少量在牵引式绳驱动上的应用，在绳驱动拟人臂上的分析目前还没有.利用拉格朗日方法建立的动力学模型具有标准的显式表达式，易于控制器的设计.文献［8－9］对并联机器人的几何形状和惯性扰动作了简化假设，利用拉格朗日方法建立了并联机器人的动力学方程.文献［10］利用拉格朗日方程建立了完整的并联机器人动力学方程.但这些学者的分析对象都是刚性机器人，针对并联式绳驱动，本文在满足要求的条件下，简化分析并建立绳驱动拟人肩关节动力学模型.

本文采用RPY(Roll-Pitch-Yaw)角描述绳驱动拟人肩关节的姿态，建立拉格朗日动力学方程，针对绳索驱动冗余的特点，且考虑到绳索的单方向受力性，提出基于最小预紧力的张力分配算法，推导出绳索的驱动力.针对机器人轨迹跟踪控制问题，设计基于Backstepping方法的系统模型控制律，并与传统的计算力矩法进行比较，在Matlab/Simulink环境下进行仿真验证.

1 机构描述

拟人肩关节是由4绳驱动的三自由度并联机器人，其样机如图1所示.

图1 绳驱动拟人肩关节样机

该机构主要由5个部件组成:运动平台、被动三自由度关节、固定平台、张力检测机构和绳索驱动机构.运动平台通过被动关节与固定平台的支柱相连接，4根驱动绳索对称分布在运动平台周围，一端固定于运动平台，另一端通过固定平台上的滑动轮和张力检测机构与基座上的绳索驱动机构相连，由驱动电机转动来带动绳长变化，控制运动平台的转动.

机构受力如图2所示，Bi，Pi(i=1～4)分别为第i根绳索与固定平台和运动平台的连接点，坐标系OBXBYBZB为基坐标系，坐标系OPXPYPZP为固定在动平台上的动坐标系，随平台的转动而变化.机构主要的结构参数包括:旋转中心到底座的高度lh，底座的长度2lb，运动平台的边长2ls和底座固定点B1B2间的距离t.

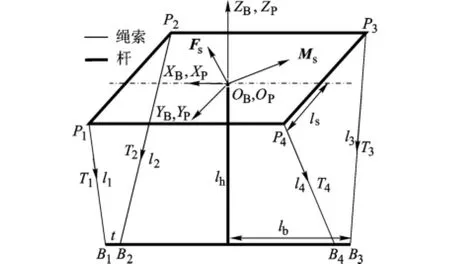
图2 机构受力示意图

2 动力学建模

2.1 机构姿态的RPY角描述

姿态矩阵是三阶的方向余弦矩阵，可用3个独立变量来表示，而这3个变量可取为绕3个轴的旋转角.采用RPY角来描述姿态矩阵，如图3所示.OPXPYPZP的初始方位与 OBXBYBZB重合(见图2).

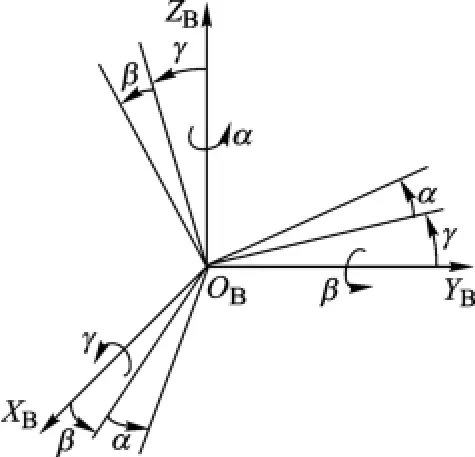
图3 RPY角示意图

首先，绕XB轴旋转γ角，再绕YB轴旋转β角，最后绕ZB轴旋转α角.由于3次旋转都是相对于OBXBYBZB而言，按照“从右向左”的合成变换原则，可得到姿态变换矩阵为

其中，R(ZB，α)，R(YB，β)，R(XB，γ)分别表示绕ZB，YB，XB轴的基本旋转变换矩阵.

2.2 动力学模型分析

由于绳索不可避免地具有一定的弹性，为了获得较好的控制效果，应当考虑绳索的弹性效应，但为了简化理论分析，不失一般性，作如下假设:①绳索变形很小，可忽略;②相对于机构平台，绳索质量很小，可忽略;③不考虑驱动器的动力学问题，假定可对关节施加任意的力矩.

在坐标系OBXBYBZB下，动平台的位置始终不变，其姿态采用RPY角描述如下:

以q为广义坐标，采用拉格朗日动力学法可建立标准形式的动力学方程如下:

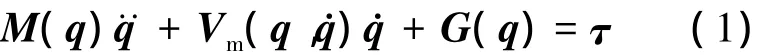
其中，M(q)为惯性矩阵;Vm(q，)为哥氏力和离心力;G(q)为势能的偏导数;τ为驱动力矩，各参数推导如下.

动平台只转动，故其动能仅包括转动动能:

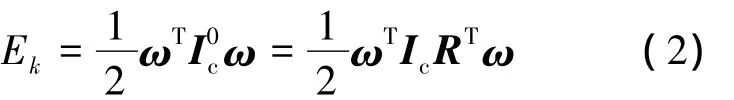
其中，R为姿态变换矩阵;Ic为绕动坐标系的转动惯量;ω为动平台的角速度，可表示为

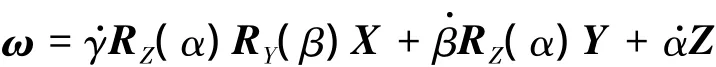
将式(2)展开，整理可得

其中，M(q)为三阶方阵，M23=M32=0，M11=IXsin2β +IYsin2γcos2β +IZcos2γcos2β，M12=M21=(IY－IZ)cosγsin γcosβ，M13=M31=－IXsin β，M33=IX，M22=IYcos2γ+IZsin2γ.

根据文献［11］，哥氏力和离心力项为

将式(5)～式(7)代入式(4)，即可推导得到Vm(q，)，亦为三阶方阵，各元素这里不再赘述.由于动平台的势能 Ep=0，因此势能偏导数项G(q)=0.

2.3 绳索张力分配

式(1)是以笛卡尔坐标q为广义坐标建立的，τ不是真正意义上的驱动力矩，是作用在(α，β，γ)方向上的广义力矩.它由支撑杆和绳索共同作用产生，可转换为绳索驱动力.

运动平台的受力如图2所示，4根绳索产生的力矩应与τ平衡.令Ms=τ，则

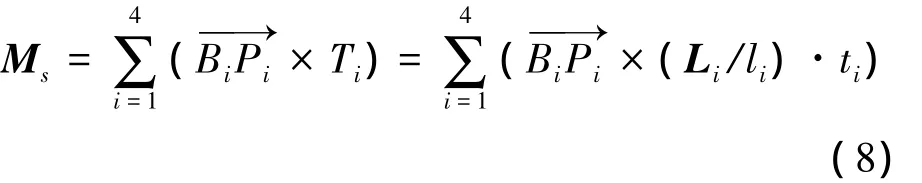
其中，ti为标量，表示绳索张力大小;Li/li为沿绳索方向的单位矢量，Li=Bi－Pi为绳长矢量.

式(9)的最小范数二乘解为

其中，(Ss)+=(Ss)T(Ss(Ss)T)－1为Ss的广义逆.

引入方程解的齐次项(λ·N∈R4×1)以调节绳索之间的张力分配，而不产生对外的作用力.

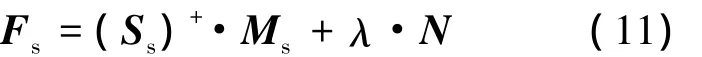
其中，N= [n1n2n3n4]T为 Ss的零空间向量，各元素可根据Cramer’s法则求得

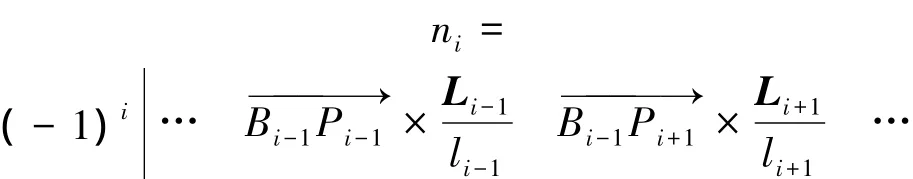
由于绳索只能承受拉力，绳驱动拟人臂机器人在运动过程中必须保持每根绳索均处于张紧状态，即绳索的张力大于零.假设绳索保持张紧所需的最小张力(即最小预紧力)为tmin，则可通过下式调节λ以使绳索张力大于tmin.

其中，N0=min|N(·)|为向量N的元素绝对值最小项;D=(Ss)+·Ms为方程的非齐次特解.

3 基于后推技术的控制律设计

基于后推(Backstepping)技术的控制律设计方法［12］的基本思路是将复杂的系统分解成不超过系统阶数的子系统，然后为每个子系统设计部分Lyapunov(李雅普诺夫)函数和中间虚拟控制量，直至完成整个控制器的设计.

令 x1=q，x2=，跟踪误差 e1=qd－q，e2=－，qd为期望值，则可得到跟踪误差状态方程为

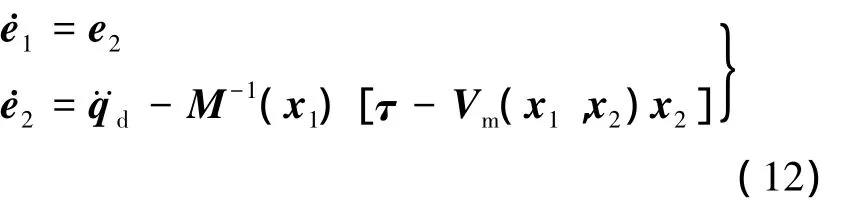
引入辅助变量 z1=e1，z2=e2－α.

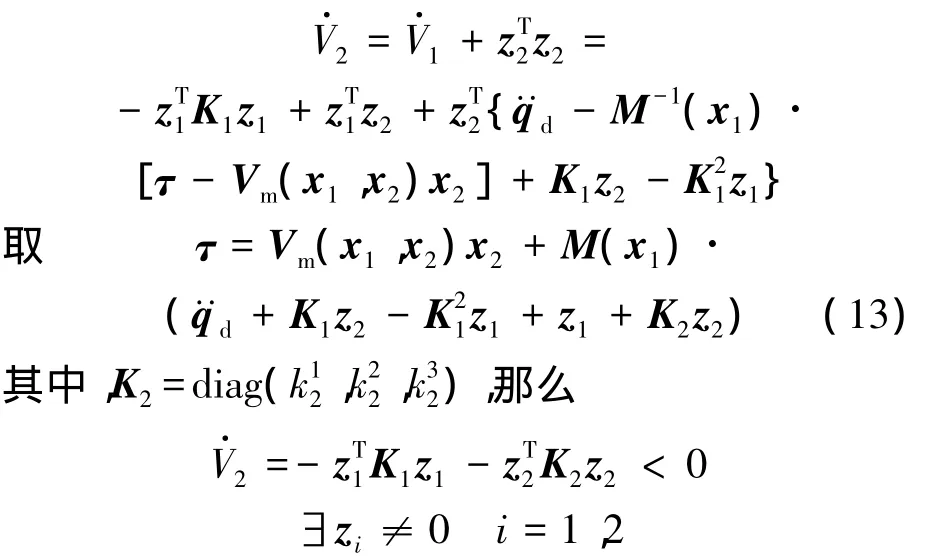
根据Lyapunov稳定性定理，由式(12)和式(13)构成的闭环系统在平衡点(e1，e2)=(0，0)处是渐近稳定的.再根据张力分配算法，可将τ转换为绳索的驱动力.

4 仿真结果及分析

虚拟样机分析软件ADAMS/View具有较为强大的建模和仿真功能，模型建好后，ADAMS可以自动计算出各部分零件的质量、质心位置及各个轴的惯性矩阵、惯性积.

在ADAMS中建立虚拟样机模型，测得绳驱动拟人肩并联机器人的相关参数如表1所示.

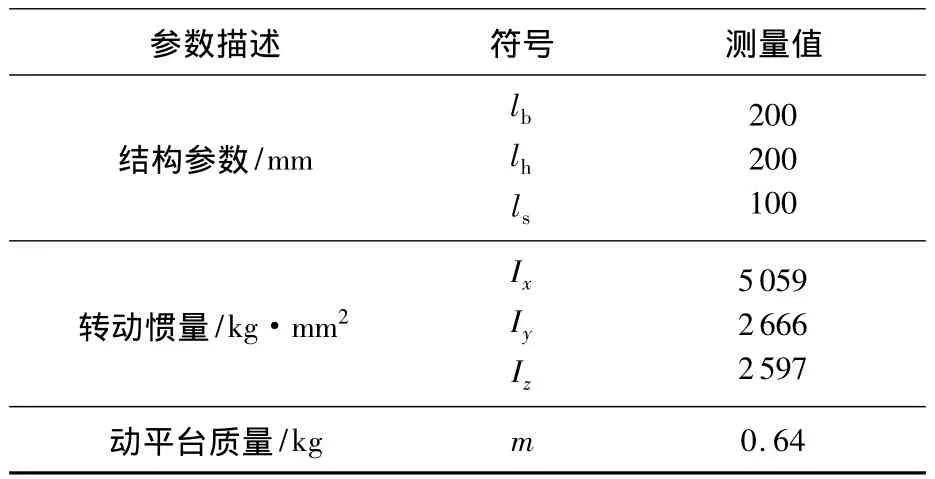
表1 机器人相关参数

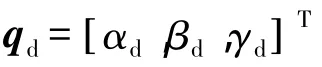
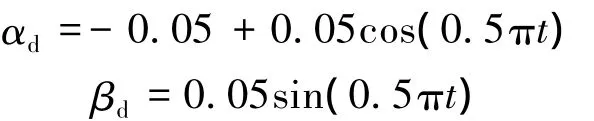
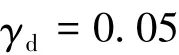
在MATLAB/SIMULINK环境下，搭建机器人仿真控制系统，利用S函数编写控制器及系统模型.分别采用本文提出的控制方法和传统的计算力矩法进行轨迹跟踪仿真实验，并对比分析.

绘制位置和速度跟踪误差曲线:图4和图5分别为计算力矩法和基于Backstepping方法的位置跟踪误差曲线，图6和图7分别是两种方法的速度跟踪误差曲线.

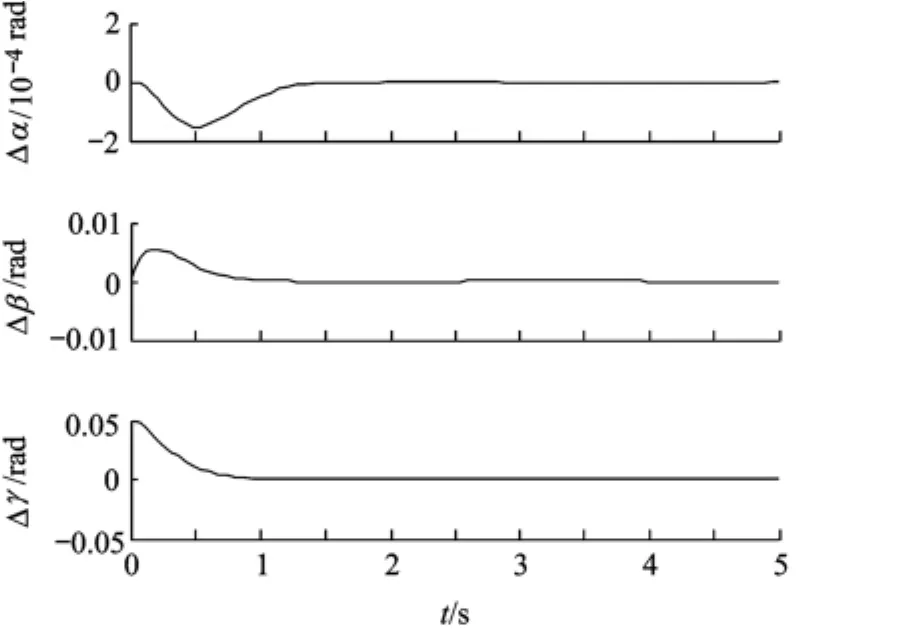
图4 计算力矩法的位置跟踪误差曲线

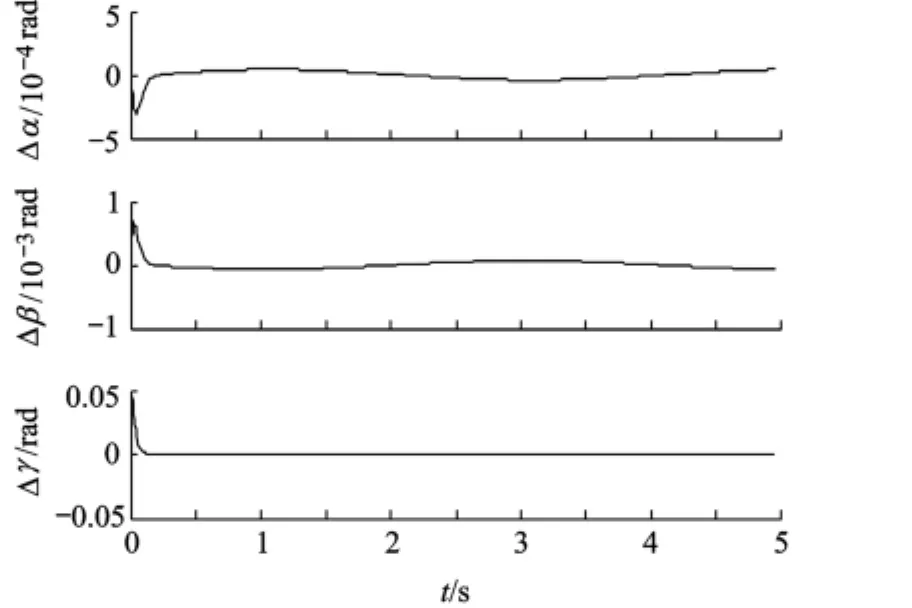
图5 基于Backstepping方法的位置跟踪误差曲线

由图4、图5可以看出，在稳态误差方面，两种方法最终都能趋于稳态;而在收敛速度方面，计算力矩法在1 s之后才趋于稳定，而基于Backstepping的方法在0.1 s就已经基本达到稳定，速度明显优于计算力矩法.本文所提出的基于Backstepping的控制方法具有较好的跟踪效果.

4根绳索的驱动力曲线如图8所示，可以看出，由于忽略了驱动器的动力学问题，在运行初始阶段，为使系统尽快到达稳态，2根绳索的驱动力较大;图中绳索驱动力的最小值为30N，实现了张力分配的预期，满足了绳索张紧的条件，说明所提出的张力分配算法切实可行;给定的整个曲线较平滑，对电动机也没有力矩的冲击.

图6 计算力矩法的速度跟踪误差曲线

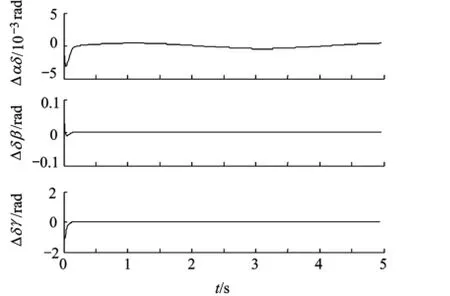
图7 基于Backstepping方法的速度跟踪误差曲线

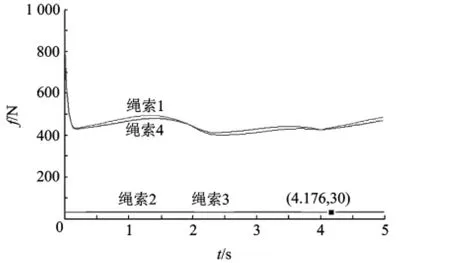
图8 绳索驱动力

5 结论

建立了拟人肩关节的拉格朗日动力学方程，提出基于最小预紧力的张力分配算法，设计了基于后推技术的轨迹跟踪控制律，并与传统的计算力矩控制方法进行对比验证，得出以下结论:①基于后推技术的控制方法在收敛速度方面明显优于计算力矩法，具有较好的跟踪效果;②由绳索驱动力曲线可知，各绳索驱动力皆能满足其张紧所需的最小张力(即最小预紧力)，表明了所提出的张力分配算法的可行性.该研究为绳驱动并联机器人的进一步有效控制和性能改进以及拟人臂整机的研究奠定了理论基础.

References)

［1］钱锡康.BUAA-RR七自由度机器人机械结构设计［J］.北京航空航天大学学报，1998，24(3):354－357

Qian Xikang.Structure design for 7-DOF BUAA-RR manipulator［J］.Journal of Beijing University of Aeronautics and Astronautics，1998，24(3):354－357(in Chinese)

［2］Jeong J W，Kim S H，Kwak Y K.Kinematics and workspace analysis of a parallel wire mechanism for measuring a robot pose［J］.Mechanism and Machine Theory，1999，34:825－841

［3］Alp A B，Agrawal S K.Cable suspended robots:design，planning and control［C］//Proceedings of IEEE Conf.on Robotics and Automation.Washington，DC，USA:IEEE，2002:4275－4280

［4］Yang Guilin，Lin Wei，Mustafa S K，et al.Kinematic design of a 7-DOF cable-driven humanoid arm:a solution-in nature approach［C］//Proceedings of the International Conference on Advanced Intelligent Mechatronics.California，USA:IEEE，2005:444－449

［5］陈伟海，陈泉柱，张建斌，等.线驱动拟人臂机器人逆向运动学分析［J］.机械工程学报，2007，43(4):12－20

Chen Weihai，Chen Quanzhu，Zhang Jianbin，et al.Inverse kinematic analysis for cable-driven humanoid arm［J］.Chinese Journal of Mechanical Engineering，2007，43(4):12－20(in Chinese)

［6］Elizabeth A B，Ying M，Sunil K A，et al.Dynamics and control of a 4-DOF wearable cable-driven upper arm exoskeleton［C］//Proceedings of the International Conference on Robots and Automation.Kobe，Japan:IEEE，2009:2300－2305

［7］陈泉柱，陈伟海，刘荣，等.具有关节角反馈的绳驱动拟人臂机器人机构设计与张力分析［J］.机械工程学报，2010，46(13):83－90

Chen Quanzhu，Chen Weihai，Liu Rong，et al.Mechanism design and tension analysis of a cable-driven humanoid-arm manipulator with joint angle feedback［J］.Chinese Journal of Mechanical Engineering，2010，46(13):83－90(in Chinese)

［8］Geng Z，Haynes L S，Lee J D，et al.On the dynamic model and kinematic analysis of a class of stewart platforms［J］.Robotics and Autonomous Systems，1992，9(4):237－254

［9］Liu K，Lewis F，Lebret G，et al.The singularities and dynamics of a stewart platform manipulator［J］.Journal of Intelligent and Robotic Systems，1993，8(3):287－308

［10］Lebret G，Liu K，Lewis F.Dynamic analysis and control of a stewart platform manipulator［J］.Journal of Robotic Systems，1993，10(5):629－655

［11］理查德·莫雷，李泽湘，夏恩卡·萨斯特里.机器人操作的数学导论［M］.北京:机械工业出版社，1998

Murray M，Li Zexiang，Sastry S.A mathematical introduction to robotic manipulator［M］.Beijing:Mechanical Industry Press，1998(in Chinese)

［12］Buhler M，Koditschek D E.A prelude to juggling［R］.Conference Presentation:26th IEEE Conference on Decision and Control，Los Angeles，California，USA:［s.n.］，1987