基于球投影的面阵探测器扭转角测量与校正

高海东 杨 民 魏东波

孟凡勇

(北京航空航天大学 机械工程及自动化学院，北京100191)

(中国科学院过程工程研究所，北京100190)

近些年来，随着计算机技术的飞速发展和面阵探测器的出现，锥束X射线计算机断层成像(XCT，X-ray Computed Tomography)技术日益成为现代无损检测(NDT，Non-Destructive Testing)领域内的研究热点［1－3］.锥束 XCT技术因其扫描效率高的优势得到了快速发展，并成功的应用到飞机涡轮叶片与火箭发动机等领域的无损检测.锥束XCT系统利用Radon正逆变换对进行重建成像［4］，这就要求重建坐标系与扫描投影坐标系保持一致，吻合的程度直接影响重建CT图像的质量［5］.但在实际系统中，探测器不可避免地存在安装误差，导致扫描投影坐标系偏离重建坐标系，影响着最终反投影地址的计算精度，造成重建图像出现伪影，丢失图像细节，影响检测结果.因此，对锥束XCT系统重建几何坐标系进行准确标定，是开展工业CT成像研究一项基础而又十分关键的工作.文献［5］提出了XCT系统的6个几何坐标配准参数，其中关于探测器的几何配准参数有:探测器绕中间行旋转角η、探测器绕中间列旋转角ξ及探测器绕中心射线的扭转角α，并针对上述3个配准参数进行了数值模拟实验，发现探测器的扭转角对重建图像的影响最大，产生了严重的伪影.本文针对探测器扭转角α，提出基于球投影椭圆轨迹的测量与校正方法，使重建坐标系达到Radon变换对的要求，消除重建伪影，保证重建CT图像的准确性.

1 探测器扭转角α测量

1.1 探测器位姿分析

FDK(Feldkamp)重建算法是目前锥束XCT成像技术的主流重建算法［6］.FDK重建算法是在图1a中射线源和探测器构造的重建坐标系Oxyz中进行的，探测器的投影坐标系为xdOdzd，算法理论上要求两个坐标系的关系为:Odzd轴平行于Oz轴，Odxd轴平行于Ox轴.然而在实际的锥束XCT系统安装中，不可避免地存在机械安装误差，导致Odzd轴不平行于Oz轴，Odxd轴不平行于Ox轴，相当于坐标系xdOdzd绕y轴旋转了一定的角度，该角度为探测器的扭转角α，如图1b所示.扭转角α的存在将给重建断层图像带来伪影［7］，造成断层图像发生形变，甚至导致特征信息丢失，影响图像的分辨力和细节的有效检出.

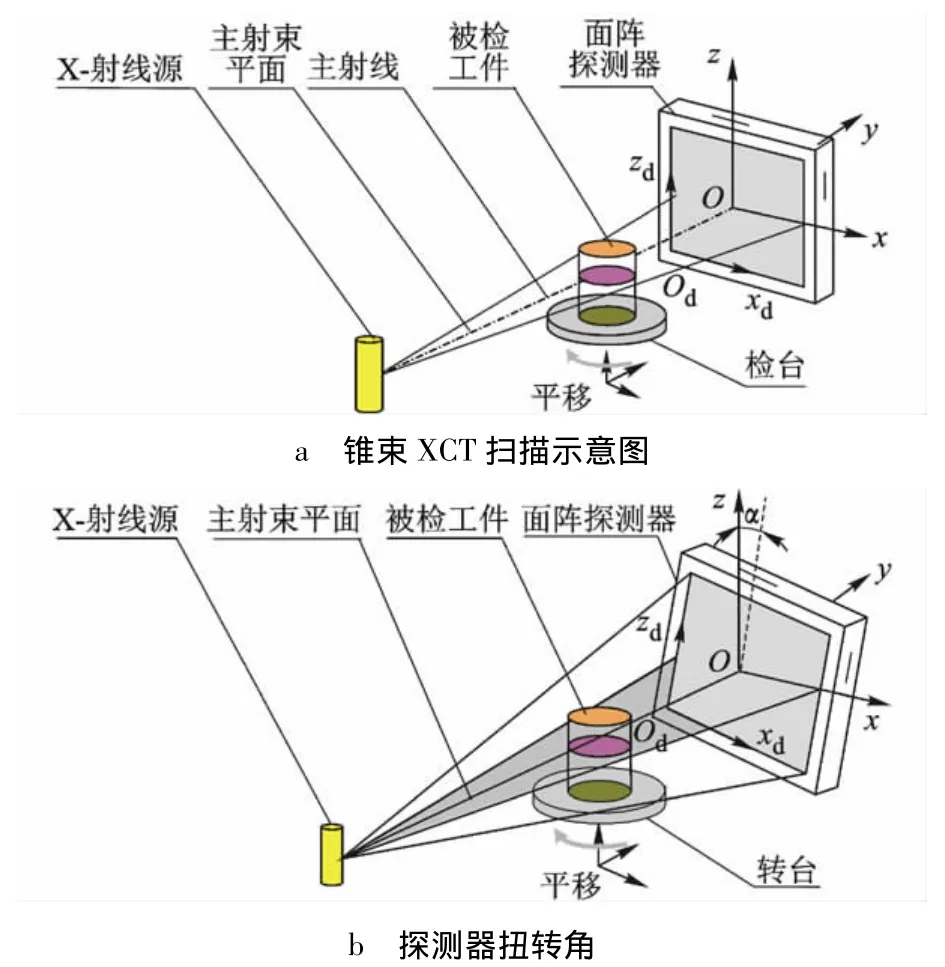
图1 投影与重建坐标系示意图

1.2 扭转角α测量方法

本文测量探测器扭转角α的方法原理如图2所示.xOz为理想状态下不存在安装误差的重建坐标系，xdOdzd为探测器存在安装误差扭转角α的探元坐标系，标志点P为非中心射束平面的空间一点，点P在转台的带动下绕转轴旋转.点P在探测器上的投影轨迹为曲线C，由检测系统的特性可知，曲线C呈现近似椭圆状.MN为该椭圆长轴所在的直线，直线l与探测器坐标系的Odxd轴平行，直线MN与直线l的夹角即为探测器的扭转角α.

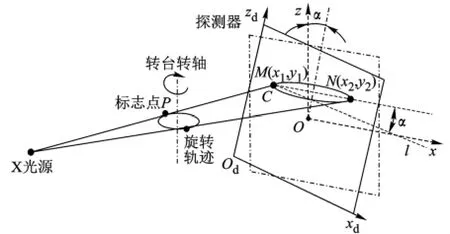
图2 探测器扭转角α测量原理图

令点 P 第 i帧投影坐标为 pi(xd－i，zd－i)，采集点 P 的多帧投影得到点集 Q={pi(xd－i，zd－i)}，对点集Q进行椭圆拟合求出探测器的扭转角α.常用的椭圆拟合方法主要有3类:基于最小二乘的拟 合 法［8］、基 于 不 变 矩 的 方 法［9］以 及 基 于HOUGH变换的椭圆拟合方法［10］.基于最小二乘的椭圆拟合方法适用性强，是曲线拟合常用方法.本文拟选择基于对称性的最小二乘法拟合椭圆方程，进而求出长轴与坐标轴的夹角.椭圆存在2条正交对称轴，其边界上至少存在2个点其外法线方向相反，这2个点互为对偶点，对偶点具有平移、旋转、缩放不变性［11］.基于椭圆的上述特性，对拟合点的采样进行优化，避免传统算法的大量无效采样，降低椭圆拟合的计算量.对点集Q，利用对偶点切线方向相同的性质选取对偶点，增大采样点落在同一个椭圆上的概率，得到采样点集Q'，Q'满足 Q'⊆Q.

椭圆的一般方程为

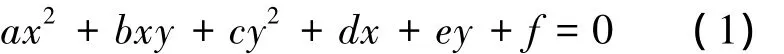
令向量 β=［x2，xy，y2，x，y］，则椭圆方程为

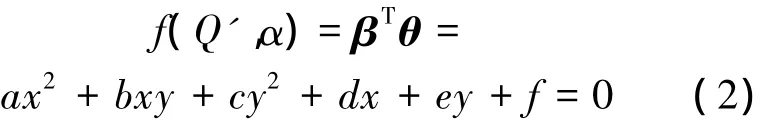
向量 θ=［a，b，c，d，e，f］决定了椭圆的形状参数，通过最小二乘拟合来寻找适合的参数向量θ，使各点到候选椭圆边缘的距离平方和最小.一般椭圆的5 个参数描述为:S={A，B，Xc，Yc，α}.其中A，B 表 示 半 轴 长，(Xc，Yc)表 示 中 心 坐标，α(－π/2＜α＜π/2)表示长轴与坐标轴正向的夹角.利用坐标的平移及旋转关系，得出 α与 θ=［a，b，c，d，e，f］的关系:

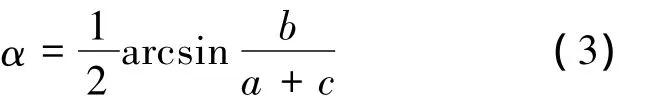
在上述思想的指导下，实验过程中可用钢珠在探测器成像平面xdOdzd上的投影质心代替标志点 P，第 i帧投影质心(xd－i，zd－i)的计算方法为

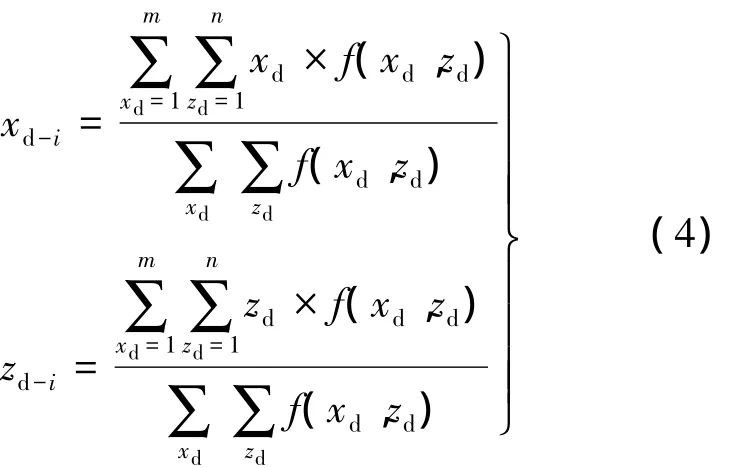
式中，m，n为投影图像尺寸;f(xd，zd)为坐标(xd，zd)处的投影值.综上所述，探测器位姿参数测算方法的流程为:采集多帧钢珠投影Q，利用式(4)求取每个钢珠投影的质心坐标(xd－i，zd－i)，根据钢珠投影质心坐标采用基于对称性的最小二乘法进行椭圆拟合，得到椭圆参数向量θ，利用式(3)求得探测器的扭转角α.

2 校正方法

由于探测器的安装误差，导致探测器并非水平竖直，从而造成重建图像伪影，在这种情况下需要进行校正.如图3所示为引入探测器扭转角α锥束XCT重建坐标系统示意图.

锥束射线视为沿z轴方向不同倾斜角度的扇束射线堆积而成，中心平面sOt上的数据重构属于扇束FBP(Filtered Backprojection)精确重建，对于非中心平面的重建，通过对扇束FBP重建公式进行修正，得到FDK重建公式.设待重建衰减系数分布函数为f(s，t，z)，视角 β下的投影值表示为 p(s，z，β).物体的衰减系数分布 f(s，t，z)可由锥束射线扫描FDK算法表示为

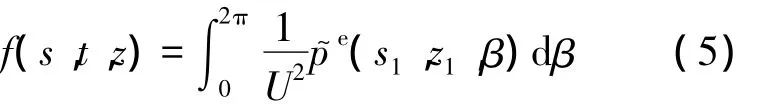
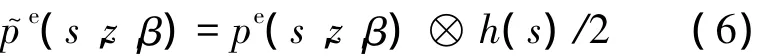
h(s)为斜坡卷积函数;pe(s，z，β)为等效投影:

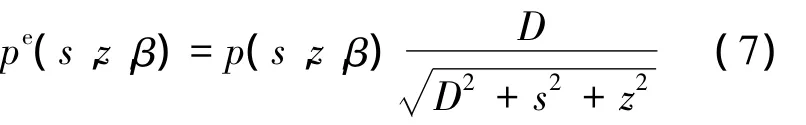
令(s1，z1)为经过待重建点(s，t，z)的射线与探测器的交点，U为加权因子，由图3所示几何关系，引入探测器扭转角α，则有

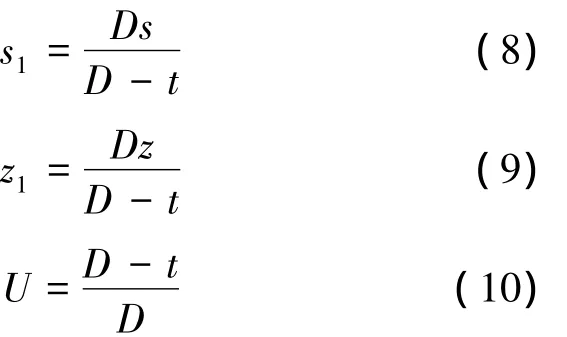
其中

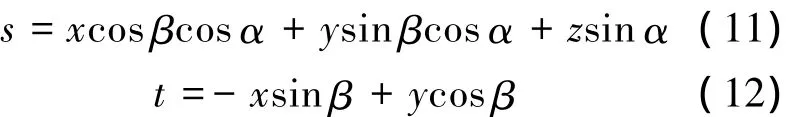
当探测器扭转角α=0°时，式(8)～式(10)退化为原始方法计算的投影地址.

由于上述方法改善了投影地址的计算，使反投影过程更加准确，从而消除了探测器扭转角对重建图像的影响.

3 实验结果

3.1 探测器扭转角测量

实验条件:钢珠直径d=10 mm置于转台上，焦距D=1200 mm，转台距探测器200 mm，钢珠距转台中心d=75 mm，高度h=57 mm，探测器尺寸为1920×1536 像素，探元尺寸:0.127 mm/像素，采集投影180帧.采用1.2节方法测量扭转角，拟合得参数向量θ各元素:

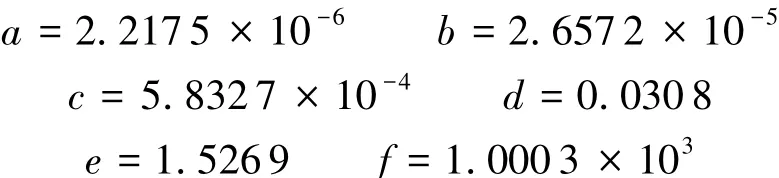
由式(3)可得长轴与 Odxd轴的夹角为:α=0.0227 rad，换算成角度为1.3006°，即扭转角 α=1.3006°.图4a所示为取对数后钢珠叠加投影.图4b所示为投影质心轨迹，虚线为椭圆长轴所在直线，实线与探测器的Odxd平行，放大部分示意椭圆长轴与探测器坐标轴的夹角α.

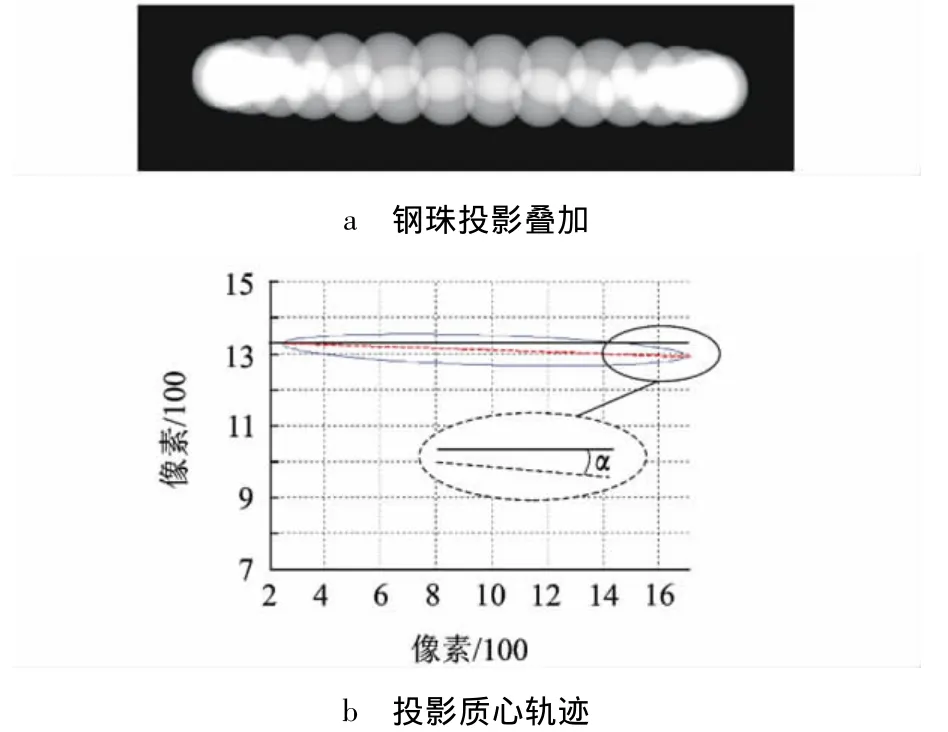
图4 探测器位姿参数测算结果

3.2 重建校正

利用上述得到的探测器扭转角，通过第2节改进的FDK重建算法进行校正.实验条件:射线源焦点尺寸0.2mm，管电压150kV，管电流2mA，焦距D=1200 mm，转台距探测器200 mm，探测器探元尺寸0.127 mm，被检对象为50 mm×50 mm×100 mm的Al，采集投影360幅.

图5a所示为利用原始FDK重建算法重建第30层得到的断层图像，图5b为在计入探测器扭转角之后利用本文方法校正得到的重建断层图像.改进算法对探测器的扭转角进行了有效校正，使得反投影地址得以精确计算，消除了由于探测器扭转角产生的伪影.对比图5a与图5b可以发现，由探测器扭转角引起的图像边缘模糊得到了很好的校正，断层图像的直角特征得到了保留.

图5 校正前后重建断层图像对比

4 结束语

本文讨论了锥束XCT扫描系统中投影坐标系与重建坐标系的配准问题，针对探测器的安装误差，提出了基于球投影的探测器扭转角的测量方法，并在三维锥束FDK重建算法的基础上，结合空间坐标变换原理，推导了相应的校正方法.校正结果表明了扭转角测量结果及重建断层图像的准确性.本文方法在实现过程中，为保证测量和校正精度，需要多帧标志点的投影，另外探测器安装误差的扭转角的旋转中心也需要正确标定，否则会导致校正效果不佳甚至重建图像错误.

References)

［1］Roberts J A，Drage N A，Davies J.Effective dose from cone beam CT examinations in dentistry［J］.British Journal of Radiology，2009，82(973):35－40

［2］Yan Guorui，Tian Jie，Zhu Shouping，et al.Fast cone-beam CT image reconstruction using GPU hardware［J］.Journal of X-Ray Science and Technology，2008，16:225－234

［3］Periago D R，Scarfe W C，Moshiri M，et al.Linear accuracy and reliability of cone beam CT derived 3-dimensional images constructed using an orthodontic volumetric rendering program［J］.Angle Orthodontist，2008，78(3):387－395

［4］Jiang Hsieh.计算机断层成像技术原理、设计、伪像和进展［M］.北京:科学出版社，2006:27－65

Jiang Hsieh.Computed tomography principle，design，artifacts and recent advance［M］.Beijing:Science Press，2006:27－65(in Chinese)

［5］侯颖.锥束XCT的定标方法研究［D］.大连:大连理工大学信息与通信工程学院，2010:28－42

Hou Ying.Research on calibration method in cone-beam XCT［D］.Dalian:School of Information and Communication Engineering，Dalian University of Technology，2010:28－42(in Chinese)

［6］Miao Hui，Wang Tingting，Zhao Huijuan，et al.Improvement based on FDK reconstruction algorithm of conebeam CT［C］//Proc of SPIE.Belingham:SPIE，2010，7570:1－7

［7］戎军艳.锥束微CT系统伪影校正与性能测试［D］.北京:中国科学院高能物理研究所，2009:62－64

Rong Junyan.Artifacts correction and performance tests of cone beam micro-CT system［D］.Beijing:Institute of High Energy Physics，Chinese Academy of Science，2009:62－64(in Chinese)

［8］邹益民，汪渤.一种基于最小二乘的不完整椭圆拟合算法［J］.仪器仪表学报，2006，27(7):808－812

Zou Yimin，Wang Bo.Fragmental ellipse fitting based on least square algorithm［J］.Chinese Journal of Scientific Instrument，2006，27(7):808－812(in Chinese)

［9］Mehmet Ali Aktas.Measuering shape ellipticity［J］.Computer A-nalysis of Image and Patterns，2011，6854:170－177

［10］Hu Xinyu，Chen Zuobing，Zhang Daode，The application of randomized hough transform in ellipse image detection［J］.Advanced Material Research，2010，159:388－392

［11］吕洪赫，姚振杰，易卫东.基于对称性的最小二乘拟合随机椭圆检测法［J］.电子测量技术，2011，34(5):37－41

Lü Honghe，Yao Zhenjie，Yi Weidong.Random least square fitting elliptic detection algorithm based on symmetry［J］.Electronic Measurement Technology，2011，34(5):37－41(in Chinese)