对数正态分布寿命型序贯验证试验方法

邓 清 袁宏杰

(北京航空航天大学 可靠性与系统工程学院，北京100191)

在产品研制周期中，为考核产品的可靠性指标是否达到一定水平，一般应进行可靠性验证试验.目前，GJB899A中已经给出了产品寿命分布为指数分布类型时的可靠性验证试验方案，Weibull分布下的定时、定数及序贯验证试验方法也已有文献可查［1－2］.但是在研究某些机械零件的疲劳寿命、尤其是维修时间的分布时对数正态分布更加理想［3－4］.对数正态分布在可靠性评估方面的应用也越来越引起重视.例如可用于描述产品在早期故障阶段的失效率［5］、荧光灯寿命分布和超大规模集成电路的失效［6］.因此有必要研究对数正态分布下产品可靠性验证试验方法.通常定时截尾试验由于便于控制试验的进程而得到采用，但试验需要的样本量较大，而定数截尾方式适用于小样本下的可靠性验证［1］.序贯试验方法相对于定时、定数截尾做出判断所要求的平均累计试验时间及平均失效数较小，可缩短试验时间和节省试验费用.文献［7］指出双参数Weibull分布下的序贯试验方案所需要的样本量为同等条件下定数试验的40%.但其缺点在于有可能出现试验时间较长而无法做出判断的情况.为解决上述问题，本文讨论当产品的寿命为对数正态分布时，在给定对数标准差的前提下，截尾序贯验证试验方案.

1 序贯验证试验程序

设产品的寿命分布为对数正态分布，其可靠度函数为

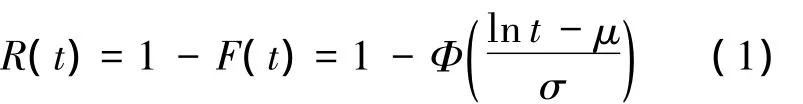
其中，Φ(x)为标准正态分布的分布函数;μ为对数均值;σ为对数标准差.

假设n个产品投入试验，其中r个失效，则联合失效密度函数为［3］

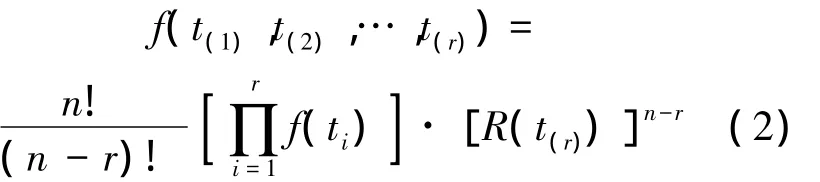
在对数正态分布下，其联合失效密度函数为

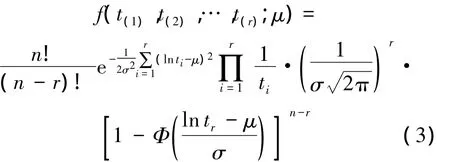
设原假设 H0:μ=μ0，备择假设 H1:μ=μ1(μ0＞μ1)，根据 GJB899A序贯验证试验的思想方法可得

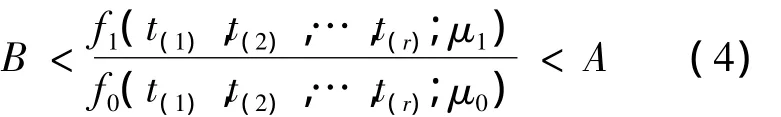
可以推导，在保证生产风险α和使用方风险β之和不增大的前提下，常数A和B可取为

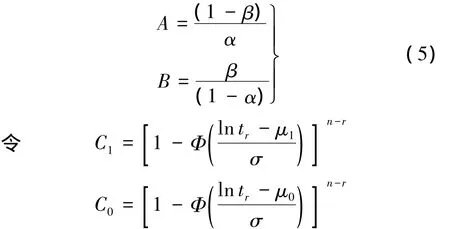
将式(3)代入式(4)并化简得

式中

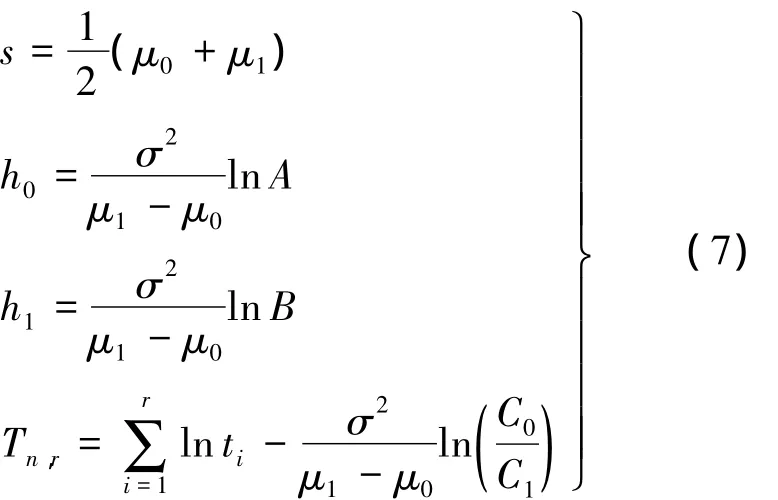
式(6)与指数分布下的序贯试验方案不同之处在于判断条件不是所有样品总试验时间，而是r个失效产品寿命的对数相加之和减去包含产品在tr可靠度信息的一个分量.

2 序贯试验的截尾

为了避免序贯试验长时间停留在继续试验区，需要对序贯试验进行截尾.设N为投入试验的样本量，r0为截尾数.显然，截尾序贯试验的生产方和使用方风险与非截尾序贯试验的有所差异.记截尾数为r0时的生产方风险和使用方风险分别为α(r0)，β(r0)，则r0越接近总样本量N，截尾的风险越接近非截尾风险.

在H0成立的前提下，当失效数为r0时，存在4种情况，其中两种不会引起误判，而两种会引起误判的情况是:

1)截尾情况下判定为拒绝H0，而非截尾情况下接受H0;

2)截尾情况下判定为接受H0，而非截尾情况下拒绝H0.

令情况1)的概率为δ(r0)，则有

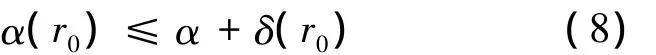
δ(r0)为以下3个事件同时成立的概率:

1)失效数r＜r0时，停留在继续试验区;

2)失效数r=r0时，满足做出拒绝判断;

3)失效数r＞r0时，做出接受判断.

其中，事件1)的概率为

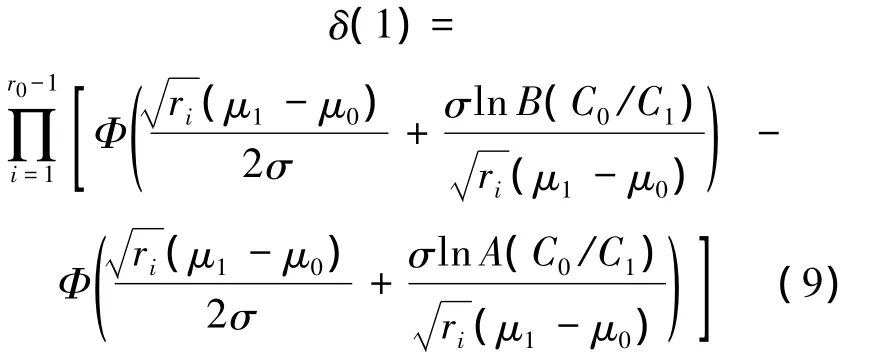
事件2)的概率为

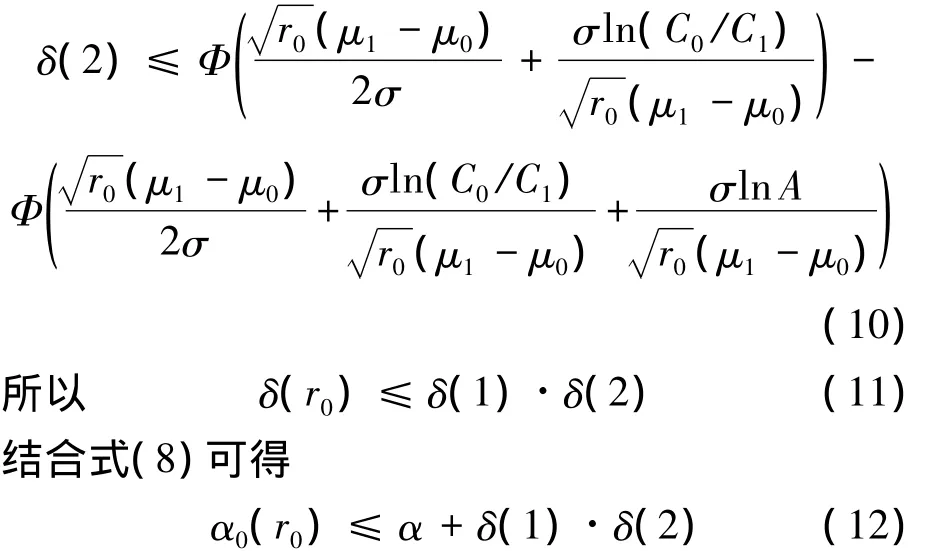
由式(12)即可确定截尾序贯试验生产方风险的上限.同理，假设H1成立的前提下，可确定截尾序贯试验使用方风险的上限.

当样本量N确定时，α(r0)，β(r0)的上限由截尾数 r0确定.因此，可调整 r0，使得 α(r0)，β(r0)与非截尾序贯下的风险值接近.由式(11)可知，截尾带来的风险增量很小.

依据上述分析当截尾数r0时作出截尾序贯试验示意图，如图1所示.

图1 截尾序贯试验示意图

从图1中可以看到，凡是穿越BD段的曲线，必定会与BC段或CD段相交.而BC段为截尾序贯试验的接受判定线，CD段为非截尾序贯的接受判定线，故可以认为若试验曲线穿越了BD段即可作出接收判定.同时，BD段延伸到与纵轴相交可得截尾时间T0，由式(6)可知T0表达式为

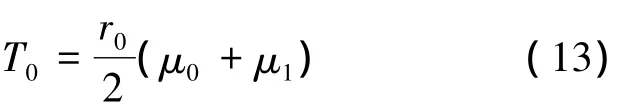
所以，以r0为定数截尾的序贯试验实际上可视为定时、定数混合截尾序贯试验.

3 试验方案的仿真评价

3.1 仿真评价方法

对上述验证试验程序的有效性，本文采用计算机模拟仿真的手段进行验证.具体步骤为:

1)通过使用MATLAB中的随机数生成函数来产生1000个［0，1］上的均匀分布随机数;

2)通过Box-Muller变换法，将产生的随机数变换为服从N(0，1)分布的随机数;

3)通过给定的α和待验证的平均寿命μ，利用式(14)将步骤2)生成的随机数转换为服从对数正态分布的随机数;

4)从这1000个数据中随机抽取N个作为投入试验的样本量，从小到大排序作为样本的失效数据，采用上述序贯验证试验程序进行判断;

5)重复步骤1)～4)一百万次，分别计算在合格质量和极限质量下的接收率，并记录平均失效数和平均等候时间.

3.2 序贯验证试验评价

以文献［8］中某种微型电机的加速寿命试验为例，其标准差为0.312，在120℃下的平均寿命为2600 h.基于上述信息，本文取其可靠度为0.9时的寿命1748 h的对数为极限质量μ1，鉴别比为d=1.5，则合格质量为 μ0=ln2622 h.在此质量水平下取生产方风险α和使用方风险β均为0.1.按照3.1节给出的方法编写了相应的计算机程序进行仿真评价.根据文献［9］中给出的正态分布下可靠性抽样检验方案，依据本次序贯试验要求计算出在定数截尾试验中的样本量应取4.为了验证本文序贯试验的有效性，参考指数分布类型下序贯试验截尾数的确定方法，进行仿真评价时样本量选取为3，4，8，12.仿真结果如表 1所示.其中，“不截尾”行对于全部样本均失效仍无法做出判断的数据组不纳入统计.μ0行表示用均值为2622 h的样本进行序贯试验时被接收的概率，μ1行表示用均值为1 748 h的样本进行序贯试验时被接收的概率.

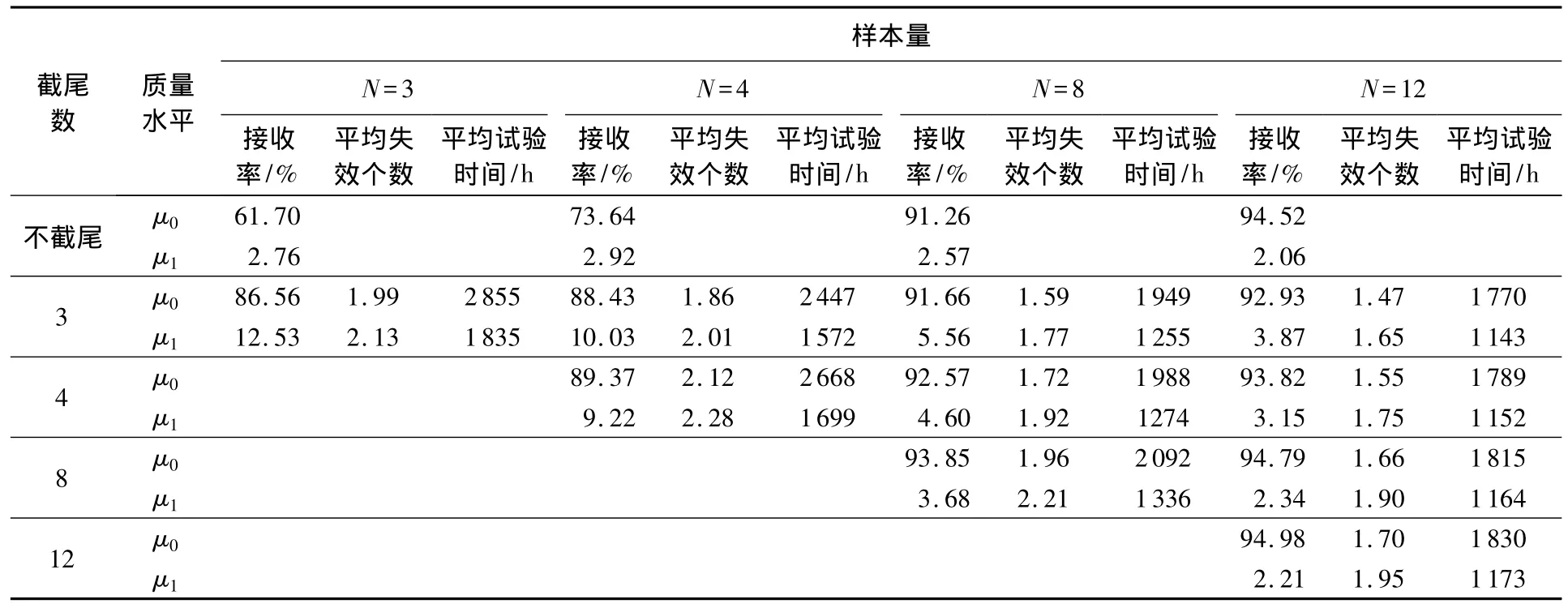
表1 序贯试验仿真评价结果

对于不截尾的情况，由于存在很多全部样本均失效仍无法做出判断的情况，表1未给出平均失效个数和平均等候时间.

从表1的数据可以得到以下结论:

1)若试验样本量较小(如取定数截尾失效数时)，截尾试验能更充分地利用试验信息做出判断，同时不会带来生产方和使用方风险的显著增加.

2)采用同样的截尾数时，样本量越大，做出判断的准确度越高，做出判断前的平均失效个数越少，平均试验时间越短.

3)当试验的样本量一定时，随着截尾数的增加双方风险都会减小，而平均失效个数和试验时间的增加却并不明显.

4)本文给出的序贯试验方案对于双方风险，尤其是使用方风险能够很好地满足要求.

当产品标准差变大时，根据文献［9］中的方法给出的定数截尾试验样本量也会增大.本文进一步的仿真评价表明，只要序贯试验样本量和截尾数不小于定数截尾试验样本量，在合格质量和极限质量下批产品的接收率都不会明显偏离预期生产方风险和使用方风险的要求.

4 结论

在批产品达到合格质量水平μ0时，依据本文给出的序贯试验方案所作判断达到并超过了1－α的要求;产品质量为极限质量水平μ1时，产品的通过率小于使用方风险.这说明本试验方案不仅能够满足试验的要求，而且能在不影响生产方风险的情况下充分保证使用方风险.给出的风险上限求解公式和仿真评价的结果都说明样本量达到定数截尾要求的2～3倍时，截尾数的适当减小不会引起实际风险超过风险控制要求，且可一定程度地缩短试验时间.本文编写的仿真评价程序亦可作为对数正态分布下确定序贯验证试验方案样本量的辅助工具.

References)

［1］陈文华，柴新，盛军鑫，等.Weibull寿命型产品可靠性定数截尾验证试验方法［J］.浙江大学学报，2001，35(2):128－130

Chen Wenhua，Chai Xin，Sheng Junxin，et al.Demonstration test plans of reliability for Weibull distribution based on censored samples type II［J］.Journal of Zhejiang University，2001，35(2):128－130(in Chinese)

［2］陈文华，柴新，石永刚.Weibull寿命型产品可靠性序贯验证试验方法［J］.仪器仪表学报，1999，20(5):493－496

Chen Wenhua，Chai Xin，Shi Yonggang.Sequential compliance method for Weibull distributions［J］.Chinese Journal of Scientific Instrument，1999，20(5):493－496(in Chinese)

［3］Guo Bo，Jiang Ping，Xing Yunyan.A censored sequential posterior odd test(SPOT)method for verification of the mean time to repair［J］.IEEE Transactions on Reliability，2008，57(2):243－247

［4］赵宇，杨军，马小兵.可靠性数据分析教程［M］.北京:北京航空航天大学出版社，2009:64

Zhao Yu，Yang Jun，Ma Xiaobing.Reliability data analysis tutorial［M］.Beijing:Beijing University of Aeronautics and Astronautis Press，2009:64(in Chinese)

［5］Lee Pei Hsi，Torng Chau Chen，Lin Yang Cheng.Determination of the optimalaccelerated burn-in time underArrhenius Lognormal distribution assumption［J］.Applied Mathematical Modelling，2011，35:4023－4030

［6］Dong Shang Chang.Optimal burn-in decision for products with an unimodal failure rate function［J］.European Journal of Operational Research，2000，126:534－540

［7］Harter H Leon，Moore Albert H，Wiegand Rudolf P.Sequential tests of hypotheses for system reliability modeled by a 2-parameter Weibull distribution［J］.IEEE Transactions on，1985，34(4):352－355

［8］茆诗松，王玲玲.加速寿命试验［M］.北京:科学出版社，1997:150－153

Mao Shisong，Wang Lingling.Accelerated life test［M］.Beijing:Science Press，1997:150－153(in Chinese)

［9］何国伟.可信性工程［M］.2版.北京:中国标准出版社，2008:588－589

He Guowei.Reliability engineering［M］.2 nd.Beijing:Standard Press of China，2008:588－589(in Chinese)