基于CE/SE法的翼型流场激波捕捉计算

崔树鑫 高 琳 高 歌

(北京航空航天大学 能源与动力工程学院，北京100191)

精确捕捉激波是计算流体动力学(CFD，Computational Fluid Dynamics)研究的重要内容.从20世纪60年代CFD的逐渐形成，到后来各种格式的不断兴起及其在计算机上的成功应用，几乎大多数研究都是围绕激波、间断等内容展开的.无论哪种格式，其主要任务都是解决单元交界面无粘数值通量的确定问题.作为迎风格式的两类典型代表——矢通量分裂格式(FVS，Flux Vector Splitting)［1］和通量差分分裂格式 (FDS，Flux Difference Splitting)［2］虽然已能较好地捕捉激波和间断，并且得到了广泛应用，但是其通量确定的复杂性，向三维推广的非精确性以及会出现非物理解等一系列问题，仍困扰着众多CFD工作者.

CE/SE方法源于20世纪90年代，由参考文献［3］提出.它将空间量与时间量统一处理，通过交错的时空网格分布，巧妙地解决数值通量的确定难题.即引入包含交界面的解元，交界面的数值通量仅由与已知求解点相关的泰勒展开式得到，既保证了界面数值通量的唯一性，又维持了时空单元的守恒性.因此，它无需方向分裂，也不需要求得黎曼解.更为突出的优点是，基于加权平均思想的空间导数求解，可以灵活地控制数值耗散.近来，新发展的 CNIS格式［4］，克服了克朗数(CFL，Courant-Friedrichs-Lewy)远远小于1时，增加的数值耗散对物理解的污染.迄今为止，CE/SE方法已成功应用于气动声学、化学反应和磁流体［5－8］等领域.而关于翼型流场的激波捕捉问题，国内外学者研究甚少.

文献［9］采用CE/SE方法对无激波的翼型绕流问题进行了数值研究，并取得了很好的结果.但是，由于守恒元和解元布置方式的特殊性，在每个时间层内只有一半空间网格点参与计算.若要分辨诸如激波等间断现象，必须提供两倍的空间网格点，大大降低了CE/SE的高分辨率特性，不适合在翼型流场中捕捉激波.为此，本文对守恒元和解元重新定义，将计算点放在网格节点和单元中心上，在一个时间步内交错计算单元、节点上的流场变量.以此为基础，对激波翼型流场进行数值模拟.通过对数值结果的讨论与分析，说明新的CE/SE方法捕捉激波的有效性和精度.

1 控制方程及新的CE/SE方法

二维无量纲欧拉方程各分量表达式为

式中，［u1，u2，u3，u4］= ［ρ，ρu，ρv，ρE］;［f1，f2，f3，f4］= ［ρu，ρu2+p，ρuv，(ρE+p)u］;［g1，g2，g3，g4］=［ρv，ρvu，ρv2+p，(ρE+p)v］;m=1，2，3，4分别对应连续方程、x方向动量方程、y方向动量方程和能量方程;ρ是气体密度;u是x方向速度分量;v是y方向速度分量;p是压力;E是单位比能量.

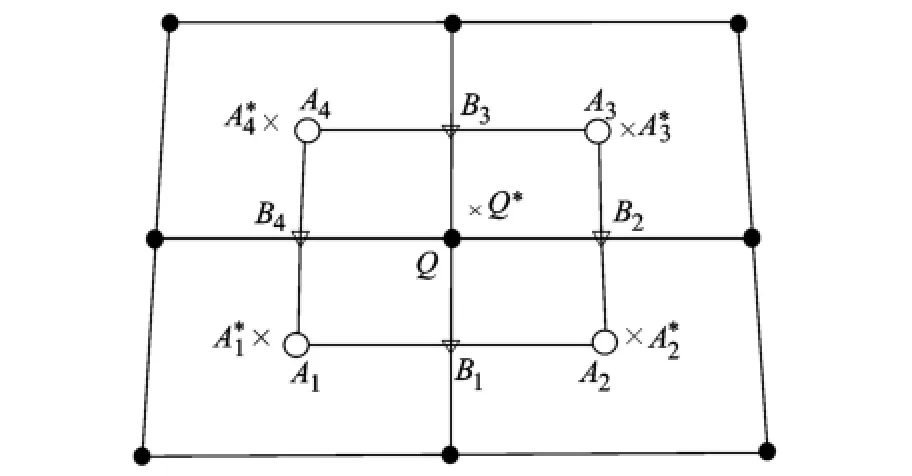
图1 空间网格

因为 (fm)Q*，(gm)Q*，(fmx)Q*，(gmx)Q*，(fmy)Q*，(gmy)Q*，(fmt)Q*，(gmt)Q*是(um)Q*，(umx)Q*，(umy)Q*，(umt)Q*的函数，由微分形式的欧拉方程(1)可知，(umt)Q*是(fmx)Q*和(gmy)Q*的函数.故而，对于任意求解点Q*，其独立的变量仅为(um)Q*，(umx)Q*和(umy)Q*.

令x1=x，x2=y，x3=t作为三维欧几里德空间E3的坐标.对方程(1)在守恒元CE(Q)上积分，并运用高斯散度定理，可得

式中，S是面 A1B1A2B2A3B3A4B4的面积;S1，S2，S3，S4，(x1，y1)，(x2，y2)，(x3，y3)，(x4，y4)分别为面 A1B1QB4，面 A2B2QB1，面 A3B3QB2和 面A4B4Q B3的面积和质心坐标.(x11，y11)，(x21，y21)，(x12，y12)，(x22，y22)，(x13，y13)，(x23，y23)，(x14，y14)，(x24，y24)，λ11，λ21，λ12，λ22，λ13，λ23，λ14，λ24，(n11x，n11y)，(n21x，n21y)，(n12x，n12y)，(n22x，n22y)，(n13x，n13y)，(n23x，n23y)，(n14x，n14y)，(n24x，n24y)分别为侧边 B4A1，A1B1，B1A2，A2B2，B2A3，A3B3，B3A4，A4B4的中心坐标、边长和外法向矢量分量.

式(3)就是新的CE/SE求解守恒变量的表达式.相应地，可以推导出以单元质心为存储点的计算公式.此外，CE/SE方法还需要计算求解点的空间导数，该计算方法与文献［10］一致，这里不再累述.至此，形成了两套分别基于单元中心和网格节点对应求解点的计算公式.在计算过程中，将单元中心、网格节点上的求解点分别放置相邻的半时间层上，通过交错的方式相互求解，从而，组成一套完整的CE/SE方法计算体系.

新方法增加了储存变量节点，相对于原CE/SE方法［10］，在一定程度上增加了计算复杂度.另外，在本文中还要用到CNIS格式，关于该格式的推导过程以及克朗数的计算方法参见文献［11］.

2 计算结果及分析

本文采用两个算例对新CE/SE方法在翼型流场中捕捉激波的能力进行分析和验证，同时，与原方法的计算结果进行了比较.根据文献［8］的结论，在以下算例中，均采用CNIS格式和当地时间步长法(CFL=0.5)，加权平均因子取为2.

2.1 NACA0012有攻角跨音流动

采用C型网格，网格数为265X45(翼型周向布置147个节点)，计算域的上下边界与翼型中线的法向距离为20倍翼型弦长，下游边界距离翼型前缘40倍翼型弦长，翼型弦长取为1，后缘采用文献［12］的处理方法(由于翼型后缘非零厚度，将后缘延长至x=1.0089处，并将原坐标同时除以新弦长1.008 9).图3是网格在翼型附近的分布图.计算工况为 Ma=0.8，α=1.25°.

图3 NACA0012翼型网格分布图

图4给出了翼型表面压力系数的分布情况.可以看出，新方法能够很好地捕捉到翼型表面的强激波和弱激波，与文献［12］吻合良好，适合模拟含有激波的翼型流场.进一步观察发现，由于加权平均因子的选择比较合理，两种方法所引入的数值粘性均有效地抑制了激波前后的过冲和过膨胀.除了激波和后缘附近区域，两计算结果与文献的相对误差小于2%.后缘处的误差主要是网格密度不足所致.值得注意的是，新方法捕捉上表面强激波需要跨越3～4个空间网格点，而原方法需要5～6个;另外，新方法能够成功地捕捉到下表面弱激波，而原方法的弱激波被抹平得很厉害，表现为一较弱的压力陡升.究其原因，主要有以下两个方面:①原方法采用交错的时空网格布置，计算点分布在网格单元中心上，在每个时间步上仅有一半单元中心点参与计算，而采用节点/单元交互的新方法，计算点分布在网格节点和单元中心上，每一个时间步内，全部单元中心点都参与计算，相当于增加了计算点的网格密度，因而，分辨诸如激波等间断的能力强于原方法.②原方法的边界条件赋值于与边界毗邻的虚单元中心处，边界附近内单元的守恒元跨越边界，全局守恒区域大于计算域.而新方法边界条件直接设置在边界节点上，边界附近内单元的守恒元边界刚好与计算域边界重合，全局守恒区域即为计算域本身.因此，从守恒性角度出发，后者更好于前者.为更精确地反映CE/SE方法捕捉激波的能力，表1列出了新方法在翼型附近激波后马赫数的计算值，并与由朗金-雨贡纽(R-H)关系得到的理论值进行对比.可以看出，新方法计算结果的相对误差不超过5%.

表1 激波后马赫数对比

2.2 RAE2822有攻角跨音流动

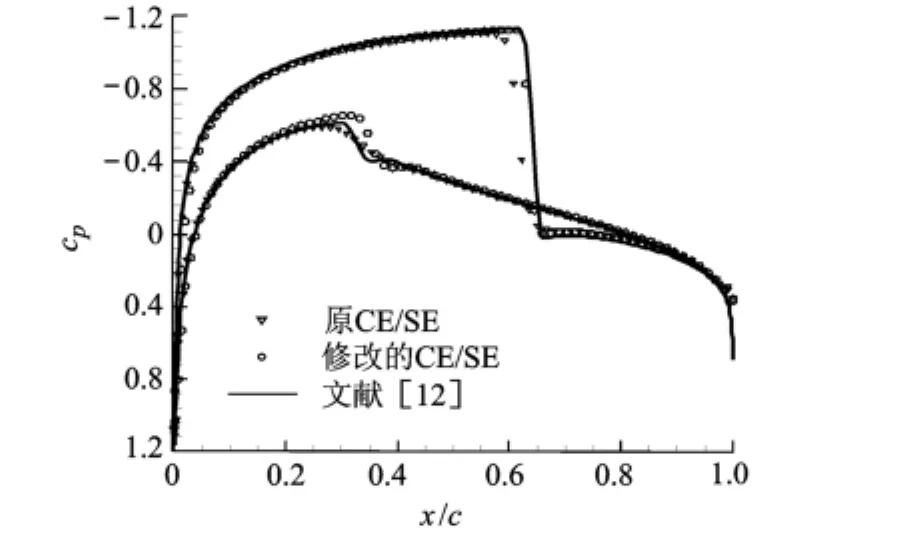
图4 算例1的表面压力系数对比曲线

为了进一步考察新方法的普适性，对典型的超临界翼型RAE2822的激波流动特征进行数值模拟.超临界翼型是一种为提高临界马赫数而采取的特殊翼型，能够使机翼在接近音速时阻力剧增的现象推迟发生，因此，精确捕捉激波位置对超临界翼型的研究具有十分重要的意义.本文采用C型网格，网格数为265×45(翼型周向布置147个节点)，翼型弦长取为1，计算域的上下边界与翼型中线的法向距离为20倍翼型弦长，下游边界距离翼型前缘20倍翼型弦长.图5是网格在翼型附近的分布图.计算工况为 Ma=0.75，α=3.0°.

图5 RAE2822翼型网格分布图

图6和图7分别是翼型表面压力分布情况和新方法计算得到的马赫数分布云图.从中可以看出，本文的计算方法很好地模拟出了气流在翼型上表面前缘膨胀加速，而后相对平缓流动，直至加速出现激波、压力骤升的整个过程.两种方法计算结果与文献［12］吻合良好，在翼型前缘上表面，原CE/SE方法的结果有些膨胀过度，在后缘区域，由于本文的网格密度远远小于参考文献的网格密度(320×64，O型网格)，两种方法的结果均与文献存在差距.而在其他区域，其相对误差均小于1%.加权平均引入的数值耗散对激波附近解的过冲和过膨胀现象有明显的抑制作用.新方法捕捉的激波跨越3～4个空间网格点，而原方法则需5～6个，进一步证实了新方法在激波分辨率方面的改进是有效的.从结果也可以看到，在不采用CNIS格式的情况下，新CE/SE方法的激波分辨率仍高于原方法.表2列出了激波位置计算值的对比情况，可以看出，两种结果都十分接近文献［12］，相对误差不超过1%.

图6 算例2的表面压力系数对比曲线

图7 新CE/SE方法计算得到的马赫数分布云图

表2 激波位置

3 结论

1)通过对不同跨音翼型流场的激波捕捉算例进行验证，说明新CE/SE方法对翼型流场捕捉激波具有适用性.

2)对原CE/SE方法的改进是有效的，可以明显提高捕捉激波的分辨率.

3)CE/SE方法能够有效地抑制激波前后的数值震荡，避免发生过冲和过膨胀现象.

References)

［1］Van Leer B.Flux-vector splitting for the Euler equations［J］.Lecture Notes in Physics ，1982，170:507－512

［2］Roe P L.Approximate Riemann solvers，parameter vectors，and difference schemes［J］.Journal of Computational Physics，1981，43(2):357－372

［3］Chang S C.The method of space-time conservation element and solution element—a new approach for solving the navier-stokes and euler equations［J］.Journal of Computational Physics，1995，119(2):295－324

［4］Chang S C.Courant number insensitive CE/SE schemes［R］.AIAA-2002-3890，2002

［5］刘敏，吴克启.基于非结构网格CE/SE算法圆柱绕流气动声场模拟［J］.工程热物理学报，2009(2):227－229

Liu Min，Wu Keqi.The aero-acoustics simulation of flow around a cylinder using unstructured CE/SE scheme［J］.Journal of Engineering Thermophysics，2009(2):227－229(in Chinese)

［6］凌文辉，赵书苗，刘建文，等.时空守恒CE/SE数值方法在凹槽燃烧流动中的应用研究［J］.推进技术，2010(1):34－41

Ling Wenhui，Zhao Shumiao，Liu Jianwen，et al.Numerical investigations of the cavity combustion flow using the CE/SE method［J］.Journal of Propulsion Technology，2010(1):34－41(in Chinese)

［7］Ji Z，Zhou Y F.A comparison study of three CESE schemes in MHD simulation［J］.ChinesePhysicsLetters，2010，27(8):085201

［8］孙孔倩，樊未军，杨茂林.CE/SE法模拟爆震波点火及传播过程［J］.航空动力学报，2008，23(2):244－250

Sun Kongqian，Fan Weijun，Yang Maolin.Numerical simulation of detonation ignition and propagation progress by CE/SE method［J］.Journal of Aerospace Power，2008，23(2):244－250(in Chinese)

［9］崔树鑫，韩玉琪，高歌.二维翼型绕流的CE/SE方法［J］.北京航空航天大学学报，2011，37(1):21－24

Cui Shuxin，Han Yuqi，Gao Ge.Space-time conservation element and solution element method(CE/SE)applied to flows around 2D airfoil［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37(1):21－24(in Chinese)

［10］Zhang Z C，Yu S，Chang S C.A space-time conservation element and solution element method for solving the two-and three-dimensional unsteady Euler equations using quadrilateral and hexahedral meshes［J］.Journal of Computational Physics，2002，175(1):168－199

［11］Yen J C，Wagner D A.Computational aeroacoustics using a simplified courant number insensitive CE/SE method［R］.AIAA-2005-2820，2005

［12］Yoshihara H，Sacher P.Test cases for inviscid flow field methods［R］.Advisory Group for Aerospace Research and Development(AGARD)-AR-211，1985