基于EEMD分解的直驱式机电作动器故障诊断
刘 俊 王占林
付永领 郭彦青
(北京航空航天大学 自动化科学与电气工程学院,北京100191)
(北京航空航天大学 机械工程及自动化学院,北京100191)
机电作动器(EMA,Electromechanical Actuator)作为飞机功率电传(PBW,Power-By-Wire)作动系统的一个主要发展方向,具有集成度高、结构简单、控制精度高、动态响应快等特点,可广泛用于航空航天、航海及其他国防、民用领域.机载直驱式双余度机电作动器(DDDR-EMA,Direct-Driv-en Dual-Redundancy Electro-Mechanical Actuator)是EMA中的一种新型作动器,主要用于操纵飞机次舵面,DDDR-EMA稳定、可靠的工作是飞机正常飞行的保证.如果DDDR-EMA发生故障,会给飞行安全造成威胁.为了对DDDR-EMA实现及时的维护和保养,准确、高效的故障诊断显得尤为重要.
对DDDR-EMA进行故障诊断,关键问题是获取故障信号,提取故障特征信息,进行模式识别和故障诊断.DDDR-EMA故障信号多为非平稳动态信号,对这类信号若采用传统的时频分析方法,如短时傅里叶分析、Wigner-Ville分布、小波分析等,分析效果不理想.近年来在非线性、非平稳信号的分析领域,经验模式分解(EMD,Empirical Mode Decomposition)和集合经验模式分解 (EEMD,Ensemble Empirical Mode Decomposition)引起了广泛关注,它们能根据被分析信号的特点,自适应地提取信号的各分量和变化趋势,确定信号在不同频段的分辨率,对平稳信号和非平稳动态信号的分解都比较有效.
由于EMD存在边缘效应、模式混叠等明显不足,本文采用了 EMD的改进方法 EEMD对DDDR-EMA进行复合故障诊断研究,通过实际的滚动轴承故障和转子故障案例分析,说明如何使用EEMD从振动信号中提取故障特征,并进行耦合故障分离.
1 机载直驱式双余度机电作动器
机载DDDR-EMA是一个位置伺服系统,主要包括控制器、智能功率模块(IPM,Intelligent Power Module)、六相永磁同步电机(PMSM,Permanent Magnet Synchronous Motor)、滚珠丝杠、反馈元件(线性可变差动变压器、旋转变压器、电流传感器),结构框图如图1所示[1].
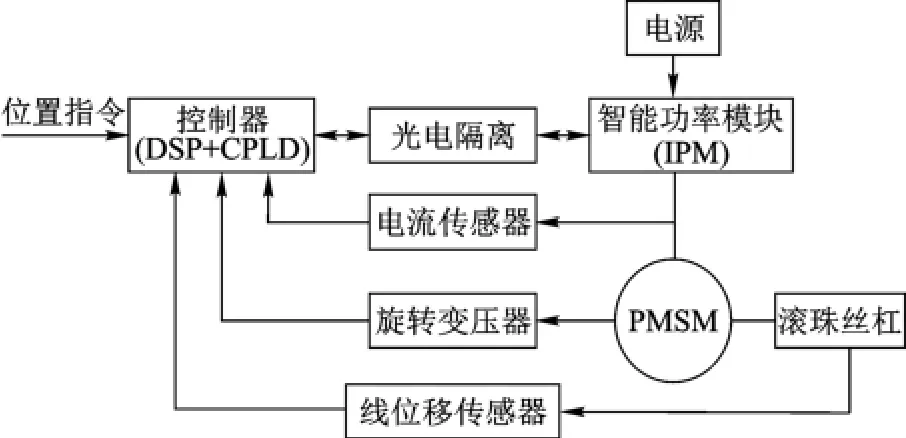
图1DDDR-EMA结构框图
DDDR-EMA机械部分结构如图2所示,它取消了齿轮减速器,将滚珠丝杠内嵌在电机转子内,由电机转子带动滚珠丝杠副的螺母旋转,再通过滚珠丝杠将转子的旋转转变成直线进给运动.直驱式的设计减少了系统的体积和重量,使系统具有更好的动态性能和传动效率.
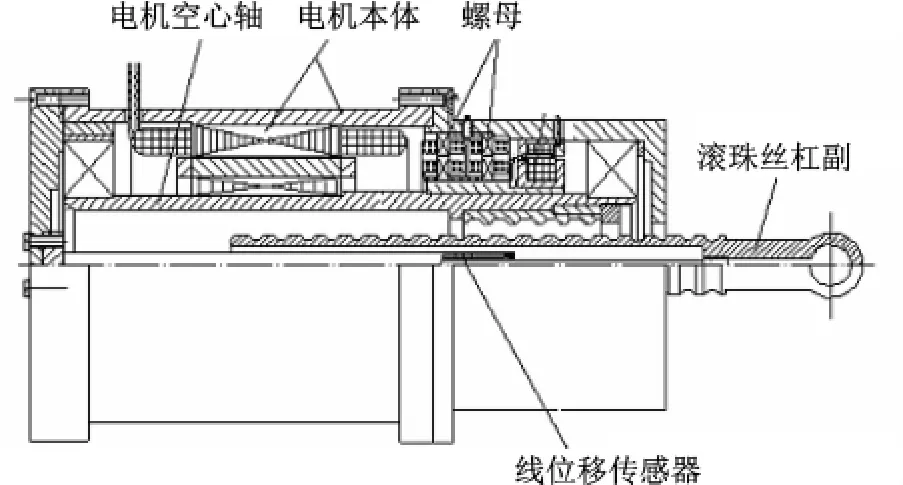
图2 DDDR-EMA机械部分结构示意图
2 EEMD方法
2.1 EMD和模式混叠
EMD是文献[2]介绍的一种非平稳信号时频分析方法,是Hilbert-Huang变换的重要组成部分.EMD主要原理是根据信号的内在特性,将信号从高频到低频自适应地分解成有限个本征模式函数(IMF,Intrinsic Mode Functions)及一个残余项之和,得出信号在不同时间尺度上的变化情况[2].
为使EMD的分解结果能够准确地体现信号的变化特征,IMF必需满足两个条件:①在整个数据序列中,极值点数必须与穿越零点的数目相等或最多相差1个.②在任一点,由局部极大值形成的上包络线和由局部极小值定义的下包络线均值为0.
EMD分解也称“筛”信号 x(t),分解步骤[3]一般包括:
1)找出所有的局部极大值点和局部极小值点,用三次样条曲线分别连接,得到x(t)上、下包络线,上、下包络线的均值记为m1(t).定义x(t)与m1(t)的差值为h1(t),则
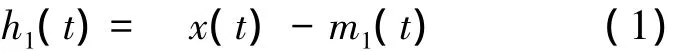
检验h1(t)是否满足IMF的两个条件,如果满足,则h1(t)是一个IMF分量;如果不满足,则需要对h1(t)做进一步筛选.
2)用h1(t)代替x(t)重复步骤1)得
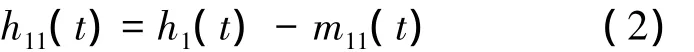
其中,m11(t)为h1(t)的平均包络线,重复操作k次,得到 h1k(t)=h1(k-1)(t)-m1k(t),直至 h1k(t)满足IMF的两个条件,得到第1个IMF分量c1.
3)定义数据序列r1(t)为x(t)与c1的差值,以r1(t)为初始数据,重复步骤 1)和 2),直到rn(t)不能再提取出IMF.信号x(t)可表示为

其中,n为所有IMF的个数;ci为IMF分量;rn(t)为分解过程的“残余量”,反映x(t)的变化趋势.
虽然EMD具有完全自适性的优点,但也存在着一些不足,如边缘效应、模式混叠.模式混叠是指单一的IMF中包含了不同频率的多个信号,或是同一个频率信号被分解在不同的IMF中[4].模式混叠主要由信号不连续性造成,信号不连续使EMD分解得到的IMF不具有真实物理含义.
2.2 EEMD 算法
为解决EMD模式混叠问题,文献[4]对EMD进行改进,提出了EEMD方法.该方法本质是对叠加了高斯白噪声的被分析信号进行多次EMD分解,利用高斯白噪声频率均匀分布的统计特性使被分析信号在不同尺度上具有连续性,从而降低各IMF分量的模式混叠程度.根据零均值高斯白噪声的特性,通过若干组IMF总体平均使加入的高斯白噪声互相抵消,还原被分析信号.
EEMD 算法归纳如下[4]:
1)初始化EMD总体平均次数M和加入的白噪声幅值系数k,令m=1.
2)执行第m次EMD分解.
①对被分析信号x(t)加入一个给定幅度的高斯白噪声序列nm(t),得到第m次加噪后的信号xm(t):
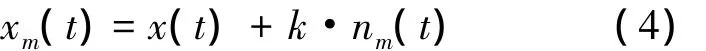
② 用EMD分解xm(t),得到一组 IMFcj,m(j=1,2,…,I).其中,cj,m为第 m 次分解得到的第 j个IMF;
③ 若m <M,则返回步骤2),m=m+1.
3)对M次分解得到的各IMF计算均值:
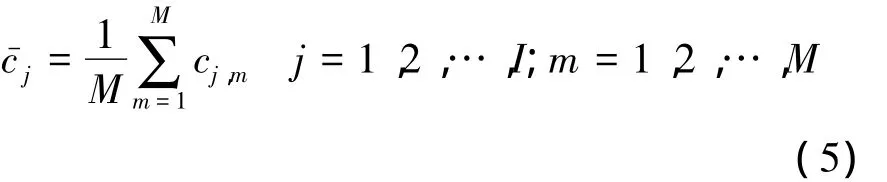
白噪声幅值系数k影响着信号的分解精度,对它应适当取值,通常 k的取值范围是 0.1~0.4.总体平均次数M影响着信号的消噪能力和计算时间,当M增大到一定值后,EEMD对信号的消噪能力增加不明显,计算时间却会明显增加.
3 基于EEMD的DDDR-EMA故障诊断
DDDR-EMA作为一种精密的机电系统,故障机理复杂.结合查阅文献[5]和总结研制过程中遇到的故障,将DDDR-EMA的故障划分为电气部分故障和机械部分故障.电气部分故障包括:控制器故障、PMSM故障、IPM故障和传感器故障.机械部分故障包括:指滚珠丝杠副发生的各种故障,一般是由设计及制造缺陷、使用中外物进入滚动体运动轨道、受到外冲击等因素造成.
PMSM是DDDR-EMA的动力驱动装置,若PMSM发生故障,则会影响DDDR-EMA的工作性能和效率,所以对PMSM故障进行诊断非常重要.在实际使用中,PMSM的故障通常不会单独发生,某些故障会连带引起其它故障,因而有必要对PMSM进行复合故障诊断研究.
滚动轴承是PMSM转子的支撑元件,滚动轴承和转子的故障很容易发生耦合,引起PMSM异常振动,表现为PMSM振动的幅值、形式和频谱的变化.所以可从发生故障的PMSM振动信号中提取故障信息,分析故障的种类和严重程度.转子故障信号与滚动轴承故障信号频谱结构不同,位于频谱图中不同频段.转子不平衡故障的特征频率处于分析信号的低频段,在频谱图中有较明显的转频及倍频特征,转速频率的高次谐波幅值很低,在时域上波形接近于正弦波.滚动轴承故障的特征频率较转子高,故障特征频率的高频分量具有调制特性.滚动轴承表面损伤会造成受损部位与其接触的零部件产生冲击,引起高频振动,滚动轴承不同的故障冲击将会导致不同的振动响应信号[6].
在分析故障信号时,EEMD先将有限幅值高斯白噪声加入故障信号,再对故障信号进行多次EMD分解,最终的IMF通过多次分解的IMF总体平均得到.利用EEMD分析故障信息,将复合故障根据各自的故障特征频率进行有效分离,提取包含故障信息的主要IMF分量.通过Hilbert变换对IMF高频分量进行包络解调,获取高频段故障信号特征;用快速傅里叶变换(FFT,Fast Fourier Transformation)变换提取 IMF低频分量故障特征[7-8];综合不同频段的分析结果,得到复合故障类型.由于转子和滚动轴承是PMSM容易发生故障的元件,故本文以转子故障和滚动轴承故障构成的复合故障为例,用EEMD进行诊断.
4 实验及分析
本文复合故障诊断实验是在课题组开发的DDDR-EMA实验台[1]上进行,主要实验设备有:DDDR-EMA工程样机、实验加载部分、加速度传感器、笔记本电脑和有故障的滚动轴承.滚动轴承型号为 K3780(主要参数:大径 D=93 mm,小径d=50 mm,滚动体个数Z=18,接触角α=0).由滚动轴承故障频率计算公式,计算得到K3780轴承内环故障特征频率为20.4 kHz,外环故障特征频率为15.6 kHz,滚动体故障特征频率为7.060 kHz,保持架故障特征频率为860 Hz.实验台的相关参数为:采样频率为48 kHz,外加负载为4.8 N·m,PMSM 转速为 2 000 r/min,每次采样 5 000点,共采集了50组数据.实验模拟的复合故障包括:滚动轴承滚动体、内环和外环故障;PMSM转子不平衡故障.
对50组采样数据标准化后进行EEMD分解,白噪声标准差取分析信号标准差的0.2倍,集合平均次数取成100.为验证EEMD方法对EMD方法的改进效果,以一组采样数据为例,分别进行EEMD和EMD分解.采样信号c(t)用EEMD和EMD分解后,均得到12个 IMF,IMF1~IMF12.由于信号特征主要集中在前几个IMF,IMF8对应信号的低频段,受篇幅限制,本文只截取了采样信号c(t)和 IMF1~IMF4,IMF8,如图 3 和图4.
图3由EEMD分解得到的IMF对采样信号c(t)分解效果较好,IMFl成分是由所加白噪声引起的;IMF2~IMF4通过M次平均,较真实体现和保存了采样信号c(t)的时域特征,各IMF分量中发生失真的情况少;IMF8为近似正弦波,对应着转子的转频成分.从图4可以看出,与采样信号c(t)相比EMD的IMF2~IMF4都存在不同程度的畸变.在IMF2中,本应属于不同频段内的频率出现在一个IMF中;而应属于同一个IMF的频率却被分到了IMF3和IMF4中,造成了频率混乱;另外IMF8的正弦成分不明显.EMD模式混叠问题导致各IMF代表的物理意义不明确,故障特征不明显,不能准确反映DDDR-EMA的工作情况.对比图3和图4的分解结果,可得EEMD有效解决了EMD存在的模式混叠现象,EEMD方法的分解结果更准确和清晰,较好地将高、低频耦合故障信号进行分离.
在图3的EEMD分解结果中,IMF2对应分析信号的高频段,滚动轴承的故障特征频率主要分布在此频段,对IMF2进行Hilbert包络解调,得到图5,为对图形清晰显示,只截取了从0~3000个采样点.从图5中可清晰看到 7 kHz,15.1 kHz和20.7 kHz高频成分,对照前面计算得到的滚动轴承故障特征频率,得知滚动轴承存在滚动体故障、外圈故障和内圈故障.对 IMF8进行 FFT变换,结果如图6,从中可以观察到33.3 Hz和66.7 Hz的转子转频和倍频,表明转子出现了不平衡故障.用EEMD分析的结果与实际故障情况相吻合.

图3 实验信号及其EEMD分解

图4 实验信号及其EMD分解
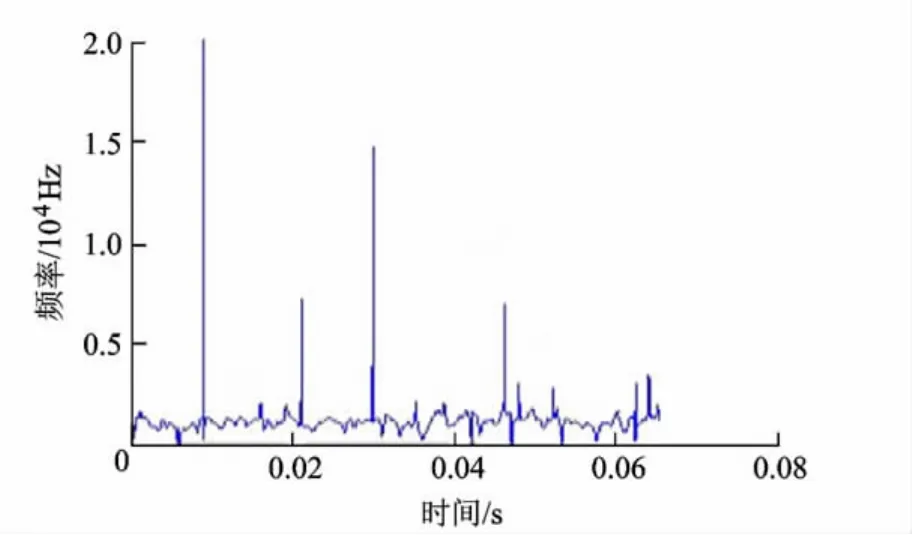
图5 IMF2包络谱(部分图形)

图6 IMF8频谱
5 结论
本文应用一种新的非稳态信号分析方法EEMD对DDDR-EMA振动信号进行处理,通过复合故障诊断实验:①比较了EEMD和EMD对振动信号的分解效果.EEMD通过加入有限幅度的白噪声,有效解决了EMD的模式混叠问题,使分解得到的各IMF具有更真实的物理含义.②采用EEMD方法进行耦合故障特征分离,对IMF低频分量进行频谱分析得到转子故障特征,对IMF高频分量用Hilbert包络解调获取滚动轴承故障特征.③运用EEMD正确提取相应的故障特征频率,准确诊断DDDR-EMA发生的复合故障.EEMD方法为DDDR-EMA故障诊断提供了一种新途径.
References)
[1]付永领,刘和松,庞尧,等.机载直驱式机电作动器的伺服控制器设计研究[J].测控技术,2010,29(7):36-40
Fu Yongling,Liu Hesong,Pang Yao,et al.Design of controller for airborne direct drive electro-mechanical actuators[J].Measurement& Control Technology,2010,29(7):36-40(in Chinese)
[2]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society,Series A,1998,45:903-905
[3]胡劲松,杨世锡,吴昭同,等.基于EMD和HT的旋转机械振动信号时频分析[J].振动、测试与诊断,2004,24(2):106-110
Hu Jingsong,Yang Shixi,Wu Zhaotong,et al.All time-frequency analysis of vibration signals in rotating machinery[J].Journal of Vibration,Measurement& Diagnosis,2004,24(2):106-110(in Chinese)
[4]Wu Zhaohua,Huang N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in A-daptive Data Analysis,2008,1(1):1-41
[5]Balaban E,Bansal P,Stoelting P,et al.A diagnostic approach for electro-mechanical actuators in aerospace systems[C]∥2009 IEEE,AC Paper,2009:1-13
[6]王胤龙.稀土永磁电机振动故障诊断系统研究[D].沈阳:沈阳工业大学电气工程学院,2008:15-19
Wang Yinlong.Research on vibration fault diagnosis system of rare-earth permanent magnet machines[D].Shenyang:School of Electrical Engineering,ShenyangUniversityofTechnology,2008:15-19(in Chinese)
[7]杨国安,许飞云,吴贞焕,等.基于小波包和解调分析的多类故障综合诊断方法研究[J].东南大学学报,2004,34(1):42-45
Yang Guoan,Xu Feiyun,Wu Zhenhuan,et al.Research on the multi-fault comprehensive diagnosis method based on wavelet packet and demodulation[J].Journal of Southeast University ,2004,34(1):42-45(in Chinese)
[8]Lei Yaguo,He Zhengjia,Zi Yanyang.Application of the EEMD method to rotor fault diagnosis of rotating machinery[J].Mechanical Systems and Signal Processing,2009,23(4):1327 -1338

