基于约束线图的超导重力梯度敏感结构型综合

贾 明 杨功流

(北京航空航天大学 仪器科学与光电工程学院，北京100191)

利用超导材料的抗磁性与超导线圈产生的磁场形成电磁力［1－2］，可使连接等效弱弹簧的质量块在重力、电磁力、弹簧力作用下保持平衡.平衡位置的重新建立会将质量块所受重力梯度的轴向分量与交叉分量信息转化为位移信息，经超导线圈转化为磁场信息后应用超导量子干涉器进行检测，通过解算可以得到高精度的重力梯度值［3］.测量载体位置的重力梯度，即可与载体惯性加速度分离，实时对重力扰动分量和垂线偏差进行估计，减小惯性导航系统误差［4］.

目前超导重力梯度敏感结构包括线性加速度或角加速度敏感单元，线性加速度敏感结构采用平行簧片式柔性移动副，角加速度敏感结构采用缺口式柔性转动副［5－7］.由于重力梯度值非常小(地球表面约为3000 E)，在测量过程中很容易受外界环境的干扰，因此需要柔性副具有较大的刚度，以提高抗干扰能力.

基于约束线图［8］分析具有单一敏感方向的敏感结构，在此基础上，提出两分量同时敏感的结构，利用并联机构形式设计柔性约束［9－10］，实现同时具有移动与转动自由度的柔性圆柱副，其中的移动自由度可以敏感重力梯度轴向分量(任一个轴向的分量需要有两个敏感结构，并沿轴向分开一定间距)，而转动自由度可以敏感交叉分量(任一轴以外两轴交叉的分量需要两个敏感结构沿任一轴向分开一定间距后再旋转90°)，将其用于超导重力梯度测量系统，具有结构紧凑、减少制冷成本、刚度大的优势.

1 超导重力梯度测量原理

地球重力场由引力场和离心力场两部分组成，重力测量即为重力加速度测量，是对重力位沿空间坐标的一阶导数进行测量，而重力梯度是重力位的二阶导数，重力梯度张量Γ可由式(1)表示为

式中，Φ为重力位;xi，xj为空间坐标.取地心坐标系为惯性系，机体坐标系为动系，则在旋转的机体坐标系测量到的比力梯度Γ'为

式中，ω=(ω1，ω2，ω3)为机体坐标系相对地心坐标系的角速度，对角线元素为重力梯度的轴向分量，其他位置元素为重力梯度交叉分量.由此可知，测量得到比力梯度与角加速度(积分得角速度)后，即可得到全张量重力梯度.

基于超导的重力梯度轴向分量测量原理如图1所示，沿轴向间隔一定距离d的两个超导材料质量块敏感各自位置的轴向重力信息，由超导回路将两个重力信息转变为两个方向的电流，则电流差反映了重力差值，应用超导量子干涉器检测此电流差，除以质量块间距，并由式(2)可解得重力梯度轴向分量.

图1 重力梯度轴向分量测量原理

同理如图2所示为基于超导的重力梯度交叉分量测量原理，两个垂直布局的超导材料转臂质量敏感各自位置的重力信息，此重力信息为垂直于质心连线(同一转臂质量转轴两侧分布质量的各自质心连线)的重力沿质心连线的交叉分量，利用两个转臂可以同时测量差模角加速度(对应比力梯度交叉分量)与共模角加速度(积分得到机体坐标系相对地心坐标系的角速度)，同样利用式(2)得到重力梯度交叉分量.

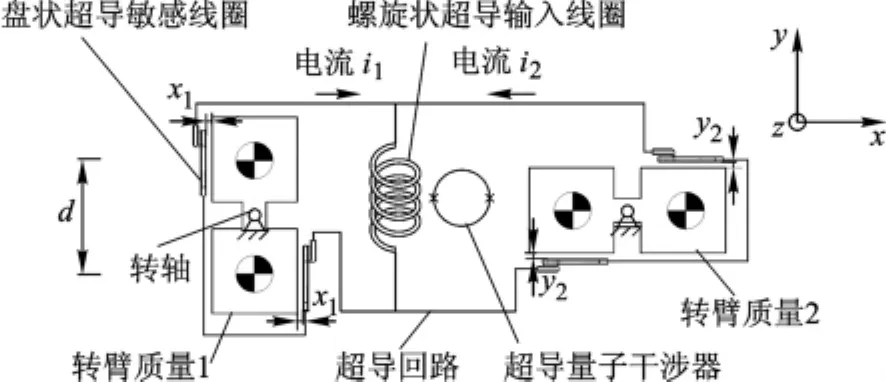
图2 重力梯度交叉分量测量原理

2 轴向分量敏感结构型综合

轴向分量敏感结构包括超导材料质量块与柔性移动副，针对柔性移动副进行型综合.基于约束线图方法可知，移动自由度等效为转心在无限远处的转动自由度.

分析两类构型:①精确约束无冗余的5约束构型，由5个柔性杆组成，或者由柔性板等效替换上面的3个柔性杆，如图3所示;②有冗余的6约束构型，如图4所示.

图3 无冗余的轴向分量敏感结构构型

图4 有冗余的轴向分量敏感结构构型

3 交叉分量敏感结构型综合

交叉分量敏感结构包括超导材料转臂质量与柔性转动副，针对柔性转动副进行型综合，同样分析两类构型:①精确约束无冗余的5约束构型，如图5所示;②有冗余的约束构型，如图6所示.另外也可直接选择缺口型柔性铰链实现转动自由度.

图5 无冗余的交叉分量敏感结构构型

图6 有冗余的交叉分量敏感结构构型

4 两分量敏感结构型综合

两分量敏感结构将质量块与转臂质量一体化，转臂质量绕轴转动用于测量交叉分量，沿轴移动用于测量轴向分量.针对同时具有柔性移动副与转动副的结构进行型综合.将图3中限制转动的约束去掉或者将图5中限制移动的约束去掉，就可以实现并联机构形式的具有移动自由度与转动自由度的柔性圆柱副，如图7所示.

图7 两分量敏感结构构型

图7中约束的实现有3种方法:①利用理想柔性细长杆;②利用两端与柔性球铰联接的刚性杆;③利用两个成垂直折角串联的柔性板.图7b图构型的3种实现如图8所示.

图8 两分量敏感结构实现

并联机构避免了在具有一个移动自由度后串联一个转动自由度的复杂形式，在构型上更为简洁、稳定性更好、对称性更好，各分支的柔性铰链产生均匀变形，可减少非对称的偏移，避免了单一铰链的应力集中.利用3对共6个敏感结构布置在正六面体全张量固定框的6个面上，可用于测量三维空间中的全张量重力梯度，其中沿z轴的敏感结构布局如图9所示.两个敏感结构沿z轴向分开一定间距后再旋转90°，移动自由度用于测量重力梯度z轴轴向分量Γ'zz，转动自由度测量重力梯度x，y轴交叉分量Γ'xy及绕z轴的共模角加速度(积分后得角速度ωz)，同理可得其他两轴测量值，由式(2)可得全张量重力梯度.

图9 沿z轴的敏感结构布局

5 仿真分析

对图8所示的两分量敏感结构进行有限元仿真，选择具有完全抗磁性的第1类超导体材料Nb，密度 8.7×103kg/m3，弹性模量 100 GPa，分析3种不同构型实现的模态.理想柔性细长杆结构的前四阶模态分析结果如图10所示.

图10 理想柔性细长杆结构模态

两端与柔性球铰相联接的刚性杆结构的前四阶模态分析结果如图11所示.

图11 两端与柔性球铰联接的刚性杆结构模态

折角串联柔性板结构的前四阶模态分析结果如图12所示.

由于不同构型柔性元件部分的具体尺寸不同，所以只对同一构型的不同模态结果进行分析，而不比较不同构型的谐振频率值.前两种结构的一阶与二阶模态分别对应移动自由度与转动自由度，且与高阶的频率差较大;而第3种结构相应的则是一阶与四阶模态，说明虽然折角串联柔性板结构在折角处形成等效约束，但在柔性板变形时约束线存在漂移，易产生非设计方向的变形，不适于在此种柔性圆柱副中使用.另外，第1种结构的三阶以上模态有明显的质量块偏移，说明柔性细长杆易发生不对称弯曲，产生非设计方向的变形.因此，两端与柔性球铰相联接的刚性杆结构更适于在此种柔性圆柱副中使用，具有两分量敏感结构所需要的移动自由度与转动自由度.

结合实际设计超导重力梯度敏感结构尺寸，如图13所示，图中尺寸单位为mm.

图12 折角串联柔性板结构模态

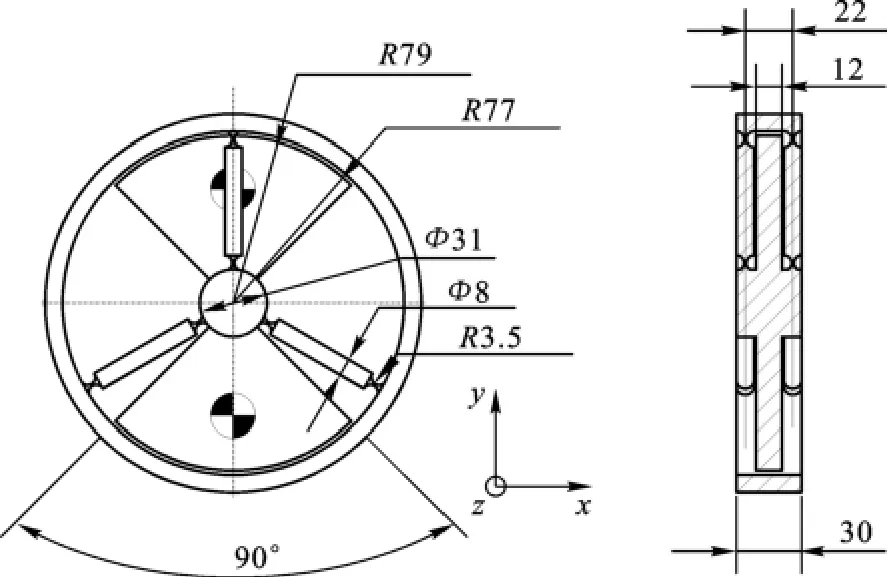
图13 超导重力梯度敏感结构

仿真分析设计(沿z轴的移动与绕z轴的转动)与寄生运动方向的刚度，以此判断设计方向与寄生方向的运动耦合情况，沿各轴的移动刚度与绕轴的转动刚度如表1所示.

表1 沿轴向的移动刚度与绕轴的转动刚度

沿z轴的设计方向移动刚度比沿其他轴的寄生方向移动刚度小3个数量级，绕z轴的设计方向转动刚度比绕其他轴的寄生方向转动刚度小约两个数量级.可见，设计方向与寄生方向的运动耦合小，另外，沿z轴的移动与绕z轴的转动不存在耦合，且可通过尺寸设计调整两种刚度的比例.因此，此种并联机构形式的柔性圆柱副适于在超导重力梯度两分量敏感结构中应用:①利用柔性机构的移动副与转动副可以方便地实现无摩擦、无间隙、高精密的运动;②自由度数越多，并联机构比串联机构在改善性能方面(尤其在结构刚性、简洁性上)的潜能越大.

6 结论

通过约束线与自由度的对偶关系，分析超导重力梯度敏感结构的型综合.结论如下:

1)对轴向分量与交叉分量敏感结构进行了无冗余与有冗余的柔性并联机构形式的型综合.在此基础上，提出了两分量敏感结构，形成了具有4约束及2自由度的并联机构形式敏感结构，避免了两种自由度的串联使用，可使重力梯度测量系统具有结构紧凑、减少制冷成本、刚度大、避免单一铰链应力集中的优势.

2)由两端与柔性球铰相联接的刚性杆并联组成的敏感结构具有独立的移动自由度与转动自由度，具有设计方向刚度小、寄生方向刚度大、运动耦合小的特点，适于在重力梯度测量系统中应用.

3)并联对称形式可减少移动轴线与转心位置的漂移，但实际加工时会存在铰链几何尺寸误差，导致各并联分支的不对称，引起微小的轴线漂移，从而对重力梯度测量精度产生影响，因此在型综合基础上还需要结合尺寸综合做进一步分析.

References)

［1］Patitsas S N.Stability analysis for axially-symmetric magnetic field levitation of a superconducting sphere［J］.Physica C:Superconductivity and Its Applications，2011，471(1):12－18

［2］南和礼.超导磁体设计基础［M］.北京:国防工业出版社，2007

Nan Heli.Foundation of superconducting magnet design［M］.Beijing:National Defense Industry Press，2007(in Chinese)

［3］Chan H A，Paik H J.Superconducting gravity gradiometer for sensitive gravity measurement.I.theory［J］.Physical Review D:Particles and Fields，1987，35(12):3551－3571

［4］Rogers M M，Huffman R E，Shearer C M.An investigation into the feasibility of using a modern gravity gradiometer instrument for passive aircraft navigation and terrain avoidance［C］//Proceedings of the Institute of Navigation，National Technical Meeting.Anaheim，CA，United States:Institute of Navigation，2009:49－60

［5］Moody M V，Paik H J.A superconducting gravity gradiometer for inertial navigation ［C］//Record-IEEE PLANS，Position Location and Navigation Symposium.Monterey，CA，United States:Institute of Electrical and Electronics Engineers Inc，2004:775－781

［6］Moody M V，Paik H J，Canavan E R.Three-axis superconducting gravity gradiometer for sensitive gravity experiments［J］.Review of Scientific Instruments，2002，73(11):3957－3974

［7］贾明，杨功流.基于超导的三位置重力梯度轴向分量测量方法［J］.中国惯性技术学报，2011，19(4):419－422

Jia Ming，Yang Gongliu.Measurement of inline-component of gravity gradient by three-position method based on superconductor［J］.Journal of Chinese Inertial Technology，2011，19(4):419－422(in Chinese)

［8］Blanding D L.Exact constraint:machine design using kinematic principle［M］.New York:ASME Press，1999

［9］于靖军，裴旭，毕树生，等.柔性铰链机构设计方法的研究进展［J］.机械工程学报，2010，46(13):2－13

Yu Jingjun，Pei Xu，Bi Shusheng，et al.State-of-arts of design method for flexure mechanisms［J］.Journal of Mechanical Engineering，2010，46(13):2－13(in Chinese)

［10］于靖军，毕树生，宗光华.空间全柔性机构位置分析的刚度矩阵法［J］.北京航空航天大学学报，2002，28(3):323－326

Yu Jingjun，Bi Shusheng，Zong Guanghua.Stiffness matrix method for displacement analysis of fully spatial compliant mechanisms［J］.Journal of Beijing University of Aeronautics and Astronautics，2002，28(3):323－326(in Chinese)