关于KCL、KVL和特勒根定理相互关系的讨论

田社平，张 峰，陈洪亮

(上海交通大学电子信息与电气工程学院，上海 200240)

0 引言

基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)是电路理论的基本规律，它们是电路理论的基石。特勒根定理也是电路基本规律的一种表述。

KCL、KVL和特勒根定理描述了电路的拓扑约束关系，三者之间的关系是:已知任意两者可推导出第三者。三者之间的关系已有多种方法可以证明[1，2]，它们或简或繁。如何找到一种简洁的，与当前电路理论教学内容表述方式相吻合的证明方式，是一个值得研究的问题。

本文在文献[3]的基础上，对上述问题进行了进一步的研究，给出了该文献结论的严格证明，同时拓展了KCL、KVL和特勒根定理三者之间相互关系的表达方法。

1 符号约定与基本结论

为分析的方便，本文先给出一些相关符号约定和电路的图的基本结论。这些内容在一般的电路教材都有叙述[4，5]。

对一个具有n个节点和b条支路的集中参数电路，其支路电压向量和支路电流向量分别用ub和ib表示，即 ub= [u1u2....ub]T，ib= [i1i2...ib]T，且各支路电压与电流采取一致参考方向。选定该电路的图的一个树，得到电路的基本回路矩阵和基本割集矩阵分别为B和Q，这两个矩阵的列所对应的支路按照先连支、后树支的次序进行排列。

树支对应的树支电压向量和电流向量分别为ut=[ut1ut2....ut(n－1)]T，it={[it1it2....it(n－1)]T，连支对应的连支电压向量和电流向量分别为uc=[uc1uc2....uc(b－n+1)]T，ic= [ic1ic2....ic(b－n+1)]T。在上述假定条件下，有下述基本结论。

(1)B和Q可分别表示为如下分块矩阵形式:

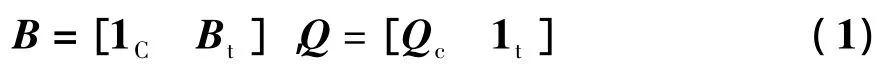
式中，1c表示一个b－n+1阶的单位矩阵;Bt是一个(b－n+1)×(n－1)矩阵;Qc是一个(n－1)×(b－n+1)矩阵;1t表示n－1阶的单位矩阵。

(2)B和Q之间满足如下关系:

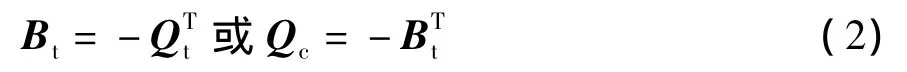
2 三者之间相互关系的表达式

对一个具有n个节点和b条支路的集中参数电路，下述关系成立[3]:

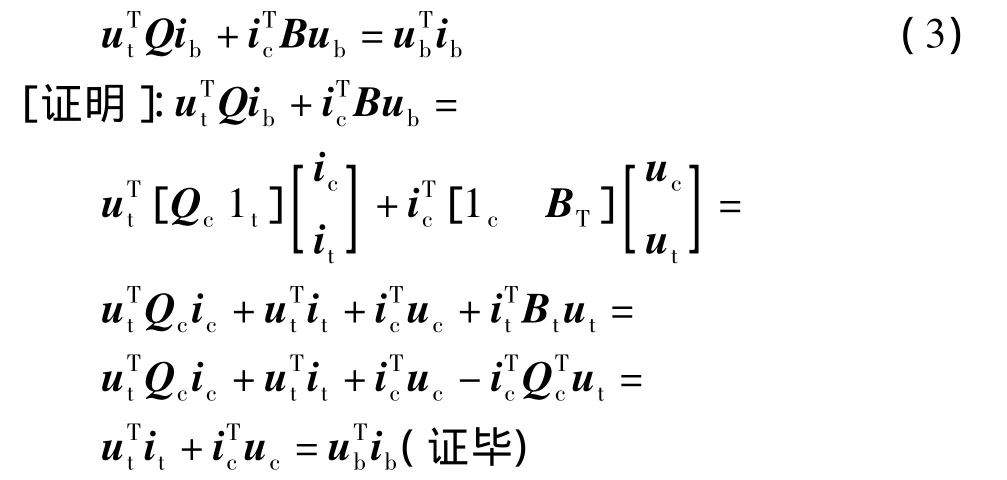
式(3)是关于KCL、KVL和特勒根定理形式一(功率守恒定理)之间相互关系的一个非常简洁的表达式。由式(3)可知，如果KCL、KVL和功率守恒定理中任意之一成立，则式(3)中的对应项为零。其中式(3)左边第一项对应KCL，左边第二项对应KVL，右边项对应功率守恒定理。因此KCL、KVL和功率守恒定理这三者中任意两者成立，则必然得出第三者也成立的结论。

从式(3)还可以得出如下推论:对一个电路，如果仅仅KCL成立，则有

由上式可以看出，此时KVL和功率守恒定理是互为充要条件的，可以相互导出。

类似地，对一个电路，当仅有KVL成立，则有

则KCL和功率守恒定理是互为充要条件的，可以相互导出。同样，对一个电路，当仅有功率守恒定理成立，则有

则KCL和KVL是互为充要条件的，也可以相互导出。

[结论]和上述分析类似，我们可以得出下述结论:

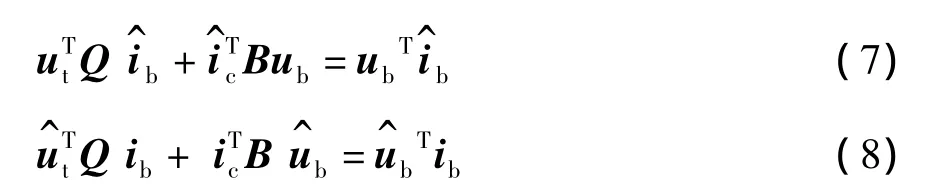
上述两式的证明类似于式(3)的证明，本文不再赘述。

式(7)和式(8)是关于KCL、KVL和特勒根定理形式二(似功率守恒定理)之间相互关系的表达式。同样从式(7)或式(8)可以看出:KCL、KVL和似功率守恒定理这三者中任意两者成立，则必然得出第三者也成立的结论。

[推论]由式(4)、式(5)和式(6)可以推论如下:

对两个具有同样拓扑结构的电路，如果仅仅KCL成立的结论。

当只有KVL成立，此时KVL和似功率守恒定理是互为充要条件的，可以相互导出。则有

此时KCL和似功率守恒定理是互为充要条件的，可以相互导出。

当仅有似功率守恒定理成立，则有

则KCL和KVL是互为充要条件的，可以相互导出。

3 结语

本文讨论的关于KCL、KVL和特勒根定理相互关系具有非常简洁的形式，这得益于电路图论和矩阵方程等数学工具的引入。在教育部高等学校电子电气基础课程教学指导分委员会制定的“电路理论基础”课程教学基本要求中，并未将基本回路矩阵、基本割集矩阵、回路方程的矩阵形式和割集方程的矩阵形式等内容列入基本内容，而是将它们列入可选内容[6]。这就意味着讲授关于KCL、KVL和特勒根定理相互关系或者解答学生相关的问题时应采用合适的形式。

笔者建议一种可行的办法是:首先提出关于KCL、KVL和特勒根定理相互关系的问题;在介绍电路图论时将基本回路矩阵、基本割集矩阵、回路方程的矩阵形式、割集方程的矩阵形式等内容作为自学内容;提示本文的方法，由学生自行探究问题的解决办法;必要时给予简要的分析。

笔者在教学实践中采取这一方法取得了良好的效果，学生普遍反映增强了他们学习电路理论或电路分析方法的兴趣，同时加深了对电路基本规律的理解。

[1]P.小彭菲尔德，R.斯彭斯，S.杜因克尔著，肖江译.特勒根定理和网络[M].北京:科学出版社.1976

[2]李瀚荪.简明电路分析基础[M].北京:高等教育出版社.2002

[3]任桂英.网络图中KCL、KVL及TELLEGEN定理相关性证明[J].北京:水利电力经济管理学院学报，1987，No.2

[4]陈希有.电路理论基础[M].北京:高等教育出版社.2004

[5]陈洪亮，田社平，吴雪.电路分析基础[M].北京:清华大学出版社.2009

[6]教育部高等学校电子电气基础课程教学指导分委员会.电子电气基础课程教学基本要求[M].北京:高等教育出版社.2011