Wait公式与Millington经验公式预测地波时延的比较

王娜，李瑞敏，苏建峰



Wait公式与Millington经验公式预测地波时延的比较

王娜1,2,3，李瑞敏1,2，苏建峰1

（1. 中国科学院国家授时中心，西安 710600；2. 中国科学院研究生院，北京 100039；3. 中国科学院时间频率基准重点实验室，西安 710600）

为了了解用于预测沿光滑分段均匀混合路径传播的地波时延的Millington经验公式的实用性，对Millington经验公式和用于预测沿光滑分段均匀混合路径传播的地波时延的严格的Wait 公式进行了比较。在Wait积分法用计算机软件实现的基础上，用上述2种方法分别计算多条实际路径的地波二次相位因子，并对计算结果进行了比较。比较结果表明，在实际工程应用中用Millington经验公式进行地波时延预测符合应用要求。

Millington经验公式；Wait积分法；二次相位因子

0 引言

均匀光滑地面的地波传播理论只适用于全海面路径或平坦均匀的全陆地路径。实际的传播路径很可能是一部分经过海面，而另一部分经过陆地，即陆海混合路径；在全陆地地波传播条件下，地波路径大多由具有不同大地等效电导率的地段组成。在这些情况下，都要采用光滑分段均匀路径的地波理论来计算地波场强和时延。常用的计算方法有Wait积分法[1]和Millington经验公式[2]，前者基于严格的地波理论，后者是半经验公式。

Wait利用2个垂直电偶极子的互阻概念及收发天线间的互易定理[3]，推导出光滑分段均匀地面地波衰减因子的公式，简称Wait积分法。在多段混合路径情况下，积分法需要计算多重数值积分，计算复杂繁琐，很不便于实际应用。与Wait积分法相比，Millington半经验公式计算简单。在实际应用中一般采用Millington半经验公式进行时延预测，但它的精确度如何？能否符合实际应用中的要求？这是很多时频工作者和用户很关心的问题。本文在路径分为3段或2段时将由Wait积分法计算得到的地波的二次相位因子与由Millington半经验公式计算得到的结果进行了比较。

1 Wait积分法衰减函数的理论表达式

在地波场强和时延的计算过程中，衰减因子的计算是整个计算的关键。J.R.Wait 从场方程出发，经过复杂严格的推导，得到了混合路径地波衰减函数的表达式。本节对混合路径地波衰减函数的严格公式作一简单介绍。

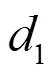
图1 光滑2段均匀路径示意图

式（1）中，

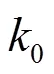
光滑3段均匀路径（如图2所示）的衰减因子严格表达式[1]为

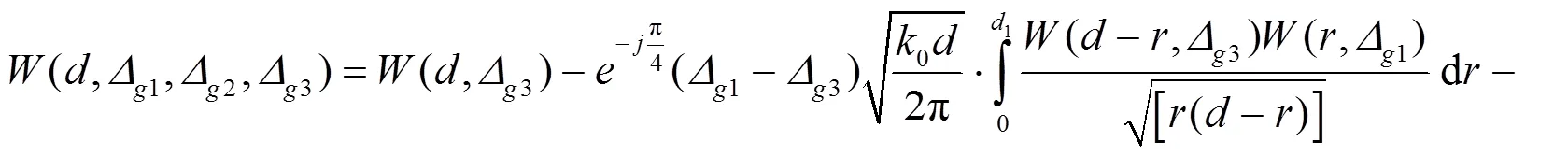
图2 光滑3段均匀路径示意图

2 Millington经验公式

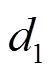
图3 光滑n段均匀路径示意图

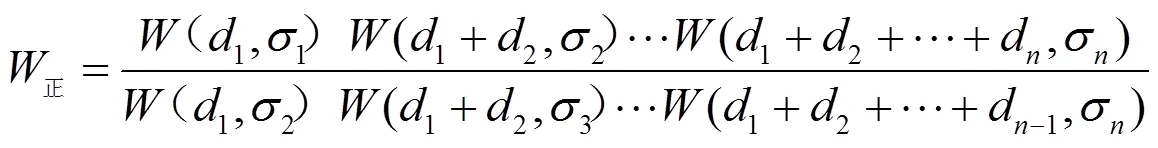
3 2种计算方式所得结果与实测结果的比较

运用1、2两节介绍的地波预测的Millington方法和严格的Wait公式，计算出了衰减因子，由衰减因子可直接求得地波的二次相位因子。分别对9条实际路径的100kHz低频地波二次相位因子进行预测。然后将计算结果分别与实际测量结果进行比较。对Wait计算公式中的积分，采用辛普森公式进行计算。

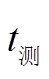
表1 发射点至接收点路径分2段时二次相位因子的计算结果及比较

本文目的是对同一地波路径比较用2种方法获得的计算结果。为此目的，在计算过程中做了一些适当的调整，说明如下：

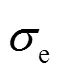
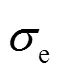
表2 发射点至接收点路径分3段时二次相位因子的计算结果及比较

4 结果分析

从表1和2中的2种计算方法所得结果可看出，在2段情况下，2种方法所得结果符合很好，在3段情况下，2种方法所得结果的偏差在0.2~0.4μs之间。所以在实际工程应用中用Millington经验公式取代严格的Wait计算公式是合理的，符合实际应用要求。

[1] 潘威炎. 长波超长波极长波传播[M]. 成都: 电子科技大学出版社, 2004.

[2] 梁仲寰. 地波场强与二次相位因子的计算方法[J]. 陕西天文台台刊(增刊), 1983, 6: 19-22.

[3] 吕保维, 王贞松. 无线电波传播理论及其应用[M]. 北京: 科学出版社, 2003.

[4] 苏建峰, 李晓珍. 关中平原大地等效电导率的间接测量[J]. 时间频率学报, 2010, 33(2): 121-128.

[5] SJ 20839—2002. 长波地波传输信道计算方法[S].

Comparison between Wait formula and Millington empirical formula for predicting ground-wave delay

WANG Na1,2,3, LI Rui-min1,2, SU Jian-feng1

(1. National Time Service Center, Chinese Academy of Sciences, Xi′an 710600, China;2. Graduate University of Chinese Academy of Sciences, Beijing 100039, China;3. Key Laboratory of Time and Frequency Primary Standards, National Time Service Center,Chinese Academy of Sciences, Xi′an 710600, China)

For learning the practicality of Millington empirical formula in predicting the time delay of ground-wave propagating along piecewise smooth mixed path, the Millington empirical formula is compared with the strict Wait integral method. On the basis that the Wait integral method is realized with computer software, the secondary phase factors for the ground-waves propagating along several paths are calculated with the Millington empirical formula and the Wait integral method respectively. The calculations are compared and the results show that the Millington empirical formula can meet the requirements of practical engineeringin ground-wave delay prediction.

Millington empirical formula; Wait integral method; secondary phase factor

TN011

A

1674-0637(2012)04-0250-05

2012-01-06

国家自然科学基金资助项目（11103025）

王娜，女，硕士研究生，主要从事低频地波场强和时延的研究。