高层结构设置TMD阻尼器减震效果

郝敬师，王静，王兴国，葛楠

(河北联合大学河北省地震工程研究中心，河北唐山 063009)

0 引 言

工程结构减震控制是指在工程结构的特定部位，装设某种装置(如隔震垫、阻尼器等)，或某种机构(如消能支撑、消能剪力墙、消能节点等)，或某种子结构(如调频质量阻尼器等)，或施加外力(外部能量输入)，以改变或调整结构的动力特性或动力作用。这种使工程结构本身及结构中的人、仪器、设备、装修等的安全和处于正常的使用环境状况的结构体系，称为工程结构减震控制体系。美国西雅图的76层哥伦比亚大厦，共安设了260个阻尼器，有效减小了风振动力反应(位移或加速度)。人们对此已经做了大量的研究［1-3］。本文根据结构动力学拉格朗日方程建立了系统的运动方程并用数值方法求解。

1 干摩擦板——复位弹簧减震系统的模型建立

TMD减震阻尼器属于被动控制(Passive Control)［4，5］，即是一种无外加能源的控制，由控制装置随结构一起振动变形而被动产生控制力。如图1所示，图中M为调谐质量，K0和C0分别为其刚度和阻尼，x0为质量块的位移。

图1 干摩擦板－复位弹簧减震系统示意图

在实际应用中，将减震系统装设在结构的顶部。坐标系xoy固定在地面上;减震系统动坐标系固定在结构上，以平衡位置为原点，如图2所示，图中H为结构的高度。

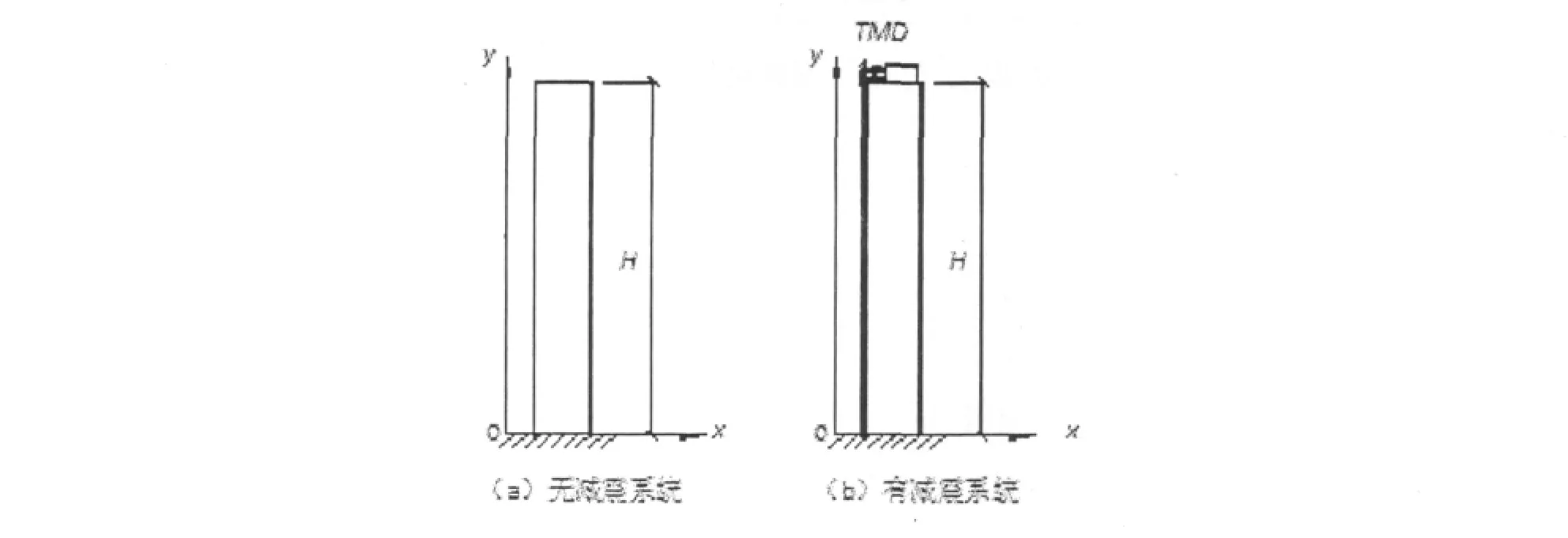
图2 超高层的简化模型

2 运动方程的建立

根据高层结构的特点，将结构简化成下端固定、上端自由的悬臂梁，并假定结构的位移具有如下的形式:

根据拉格朗日方程［6］建立减震体系的运动方程，拉格朗日方程的形式如下:

其中:T为体系动能，V为体系势能，Qqi是相应于广义坐标qi的广义力。则体系的动能与势能分别为:

式中:m是超高层体系单位高度的质量，EI是超高层的截面抗弯刚度。

令体系的广义坐标qi发生虚位移δqi，设δA为作用于体系上的非保守力所作的功，则全部非保守力做虚功为［7］:

式中:c是超高层体系单位高度的阻尼系数，为地震地面加速度。

因此可得广义力为:

分别将T、V、式(1)中，得到体系的运动方程如下:

随着汽车技术的发展与进步，传统的以经验技术为主的维修理念已经不再适应汽车发展的技术与现代客户的需求，传统维修向现代科学养护转换是必然趋势。因此以可靠性状态检测与监控是对车辆科学养护基础和原则。所以，我们一切科学养护方案必须以先诊断后维修，先检测后养护，经过科学检测—制定科学养护方案—实施科学养护工艺。就是说实施科学养护是对监测与检测数据基础之上的具有针对性的科学养护方案基础上实施的。我们的产品(服务)推广理念也是遵循这个原则。科学养护是我们核心理念，科学养护针对的是传统经验技术的变革，是我们倡导和引领发展理念，这也是我们竞争的差异性。

其中:

由于(2)式为动力耦合非线性方程组，先用行列式将其解耦，变为运动耦合的方式，才能用数值方法求解:

其中:

可以采用龙格库塔数值方法［8］应用Matlab语言［9］编程求解(3)式。

3 实例计算与结果分析

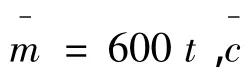
表1 阻尼系数对位移的影响(K=1000 kN/m，μ=0.01，M/m=3)

从表1和图3可以看出随着阻尼系数C0的增大，各参照点的位移逐渐减小，说明干摩擦板——复位弹簧减震系统具有很好的减震效果。当C0=105kN/m·s时，减震效果最佳，减震效率达到58.3% 。从图4可以看出，随着摩擦系数的增大，超高层的位移减小，因此，摩擦系数越小减震效果越好。

从图5可以看出，刚度系数对体系的位移影响不明显，说明弹簧对干TMD阻尼器减震系统的主要作用是使调谐质量复位，取K0=10 000 kN/m。从图6可知随着调谐质量的增大，超高层的位移逐渐增大，说明调谐质量较小时减震效果越好，但影响不明显。在本例中当M/m=1时最佳。

由以上分析可得出TMD阻尼器减震系统减震效果最佳的情况为:M/m=1，μ=0.01，K0=10 000 kN/m，C0=105kN/m·s，减震效果可达59.3%。

从图7～图9为设置TMD阻尼器减震系统的超高层体系的速度、加速度和弯矩与无减震时的比较，可以看出，该减震系统对超高层在地震作用下起到了明显的减震作用。图10为超高层最高点在减震效果最优状态下的位移时程图。

4 结论

(1)推导了超高层结构顶部采用干摩擦板——复位弹簧减震系统的运动方程用龙格库塔法求解可以得到合理的计算结果。

(2)该减震系统具有明显的减震效果，超高层的位移、加速度及弯矩都有明显的减小。但减震效果主要与阻尼系数相关，复位弹簧主要起复位作用。M/m=1，μ=0.01，K0=10 000 kN/m，C0=105kN/m·s，减震效果可达59.3%。

(3)在结构顶部设减震系统的减震效果不如在结构基础顶面设置隔震支座明显［7］，但具有安装方便，更换、维修容易的优点。

［1］周福霖.工程结构减震控制［M］.北京:地震出版社，1997.

［2］Sladek J R，Klinger R E.Effect of tuned mass dampers on seismic response［J］.J.Struct.Div，1983，109:2004-2009.

［3］J.P.T.Yao.Concept of Structure Control of Structure Division［J］.ASCE 98.1567-1574(1972).

［4］潘琴存.摩擦摆TMD减震结构的动力分析与试验研究［D］.华中科技大学，2006.

［5］汪源浩，沈小璞，王建国.超高层建筑结构的减震控制技术与抗震设计要点［J］.合肥工业大学学报(自然科学版)，2006，29(3).

［6］邹经湘，于开平.结构动力学［M］.哈尔滨:哈尔滨工业大学出版社，2009.4.

［7］葛楠，苏幼坡，王兴国等.竖向刚度对FPS滑移摩擦摆系统隔震性能影响研究［J］.工程抗震与加固改造，2010，32(4)，20-25.

［8］李庆扬，王超能，易大义.数值分析［M］.北京:清华大学出版社，2008.12.

［9］原思聪.MATLAB语言与应用技术［M］.北京:国防工业出版社，2011.8.

［10］Satish Naga rajaiah，Ertan Sonmez.Structures with seismictive variable stiffness single/Multiple tuned mass dampers［J］.Journal of Structural Engineering，2007，133(1):67-77.