单跨双层山形门式刚架的整体稳定性分析

杨忠华

0 引言

稳定性分析是钢结构性能分析的主要内容[1]。轻型门式刚架是工业厂房应用较多的一种结构形式，对其整体稳定性的验算通常采用计算长度法。门式刚架的计算长度系数是在门式刚架的柱顶加集中力，在忽略梁的轴力下按照有侧移失稳的特征值方法求得的[2]。

但是人们发现在一些特殊的情况下，如斜梁轴力大以及考虑非线性的情况下，实际结果与传统的计算有较大差异，为此一些学者对门式刚架计算长度问题进行过研究[3]，但大都局限于单层单跨及单层双跨刚架，而对单跨双层刚架的研究所见不多。

本文对此进行了一些研究，主要通过传统的近似法求单跨双层的屈曲荷载及用有限元软件对单跨双层山形门式刚架的稳定性在考虑梁轴力的情况下进行特征值线性屈曲分析，并对两种情况的结果进行比较，分析了影响该结构失稳及梁柱计算长度系数的因素，提出了该类型刚架失稳时梁柱计算长度系数的简化计算公式，为实际工程应用提供依据。

1 单层双跨山形门式刚架计算模型

本文取单跨双层钢结构厂房的一个截面图。屋顶坡度为1∶10，二层的荷载设计值 q1=70 kN/m，顶部屋面荷载设计 q2=7 kN/m，L=15 m，Hc1=Hc2=15 m，如图1所示。

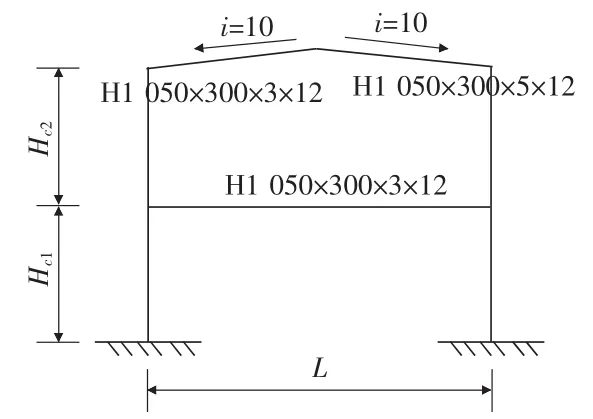
图1 单跨双层山形门式刚架形式

2 传统计算方法

按现有的规范方法来计算稳定性[2]，对于这样的纯框架结构在一般的设计中都作为有侧移的框架处理。框架柱的计算长度系数如下:

对于一层柱:

柱k1=0.709，k2=∞。查GB 50017-2003得有侧移时边柱μ =1.22。

对于二层柱:

柱 k1=0.045，k2=0.709。查 GB 50017-2003 得有侧移时边柱 μ =2.21。

对于斜梁:

由于上述计算长度系数是在斜梁轴力为零的情况下求得的，即表示无需计算斜梁平面内稳定，斜梁的计算长度系数不能求出(斜梁的计算长度为∞)。

3 单跨双层刚架的特征值屈曲分析

通过计算我们发现按有限元计算出结果与按GB 50017-2003查表的结果有较大误差。二层斜梁所受轴力相对于其截面尺寸来说不容忽略，会对整体结构的稳定性产生巨大影响，为了搞清楚这种结构的稳定特性，我们对这种形式的结构进行了大量的整体稳定分析，发现二层荷载与顶层荷载的比值β，以及各个柱的刚度k对结构的稳定有很大的影响。

3.1 参数β变化对结构稳定性的影响

表1 列出了当 k1=0.05，k2=0.71 时，β 取 10，20，30，50，70，100时如图1所示结构的各柱及斜梁计算长度系数。

在表1～表4中我们定义:

μ1:第一层柱的计算长度系数;

μ2:第二层柱的计算长度系数;

μx:斜梁的计算长度系数。

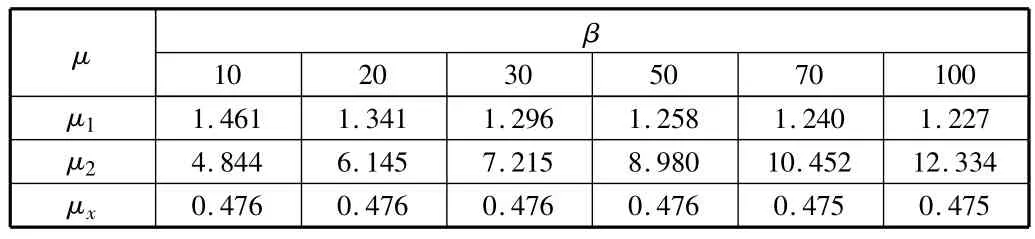
表1 当k1=0.05，k2=0.71时，β变化时的斜梁和柱的计算长度系数

由一阶模态图分析可知结构主要以有侧移形式失稳。可以发现β的变化对结构的稳定有非常大的影响，当β由小逐渐变大时，一层柱长度系数减小。而对于上层柱子长度系数增大的非常快。

3.2 参数k1变化对结构稳定性的影响

表2列出了当β=30，k2=0.71时如图1所示结构的各柱及斜梁计算长度系数。

表2 当β=30，k2=0.71时，k1变化时的斜梁和柱的计算长度系数

由一阶模态图分析可知当取β=30，k2=0.71时，结构以有侧移形式失稳。k1对一，二层柱子的影响不是很大。它对斜梁的长度系数有较大影响。

3.3 参数k2变化对结构稳定性的影响

表3列出了当β=30，k1=0.045时如图1所示结构的各柱及斜梁计算长度系数。

由一阶模态图分析可知当取β=30，k1=0.045时，结构以有侧移形式失稳。

3.4 单跨双层山形门式刚架线性状态下的梁柱的计算长度系数拟合公式

由上述分析可见对于单跨双层框架，当斜梁刚度较弱，受力较大时，不应该忽略斜梁轴力对结构稳定性的影响，此时按照规范去查找柱的计算长度系数，由于忽略了斜梁的轴力，则会产生较大误差，对于这种结构必须用整体分析方法。

表3 当β=30，k1=0.045时，k2变化时的斜梁和柱的计算长度系数

为了便于应用，在前面对该结构做的整体分析的基础上，对所得到的数据进行分析，对柱、梁的计算长度系数做了线性回归，得到了有良好精度的公式:

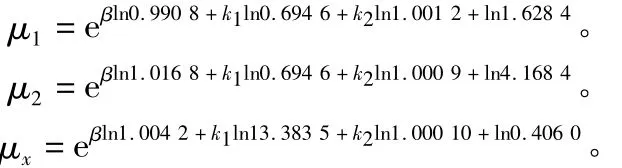
为了验证公式的精度，本文将有限元特征值法求得的值和用拟合公式计算出的值做了比较，比较结果见表4。可见拟合公式具有较高精度。

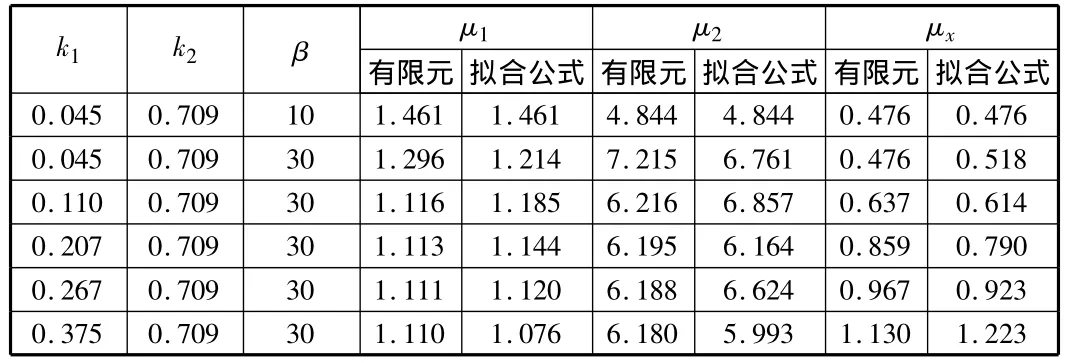
表4 有限元特征值法求解结果和拟合公式计算得到的值的比较

4 结语

1)分析单跨双层门式刚架稳定性问题时，不应忽略斜梁轴力的影响。

2)影响单跨双层门式刚架整体稳定性的因素有二层荷载与顶层荷载的比值β，以及各个柱的刚度k。

3)考虑斜梁轴力影响时，梁柱计算长度系数可用下面公式近似表示:

[1]陈惠发.钢框架稳定设计[M].周绥平，译.上海:世界图书出版公司，1999.

[2]GB 50017-2003，钢结构设计规范[S].

[3]李国强，王静峰.无侧移半刚性连接组合框架的稳定分析:(I)柱的计算长度系数方程[J].力学季刊，2006(3):17-18.

[4]陈 骥.半刚性刚架的梁柱连接性能和稳定设计[J].建筑结构，2004(S8):59-67.