位置基准的分布对GPS 网优化设计的影响分析

刘明辉

0 引言

控制网的优化设计问题在测量界一直是一个经典的研究课题。GPS网的优化设计是实施GPS测量的基础工作，它是技术设计所需达到的合理程度的一种状态描述[1］。经典的设计理论未顾及到建网的费用指标，并不能算得上是真正的最优化网。因此，所谓的最优网，应该是在能够满足用户对网的精度、可靠性要求的基础上，尽量使用较低成本的控制网。

现如今，用户对测绘成果的需求已经不仅仅只停留在高质量层面上，同时还要求消耗低成本。因此，如何在保证适当的质量控制指标的同时，将消耗成本降到最低，提高项目的效益，进行全面综合的控制网优化设计，是一个值得研究的课题。

1 GPS控制网的数据处理

GPS网的数据处理大体可划分为数据采集、数据传输、格式转换、数据预处理、基线解算和网平差几个阶段[2］。

1.1 数据预处理

基线解算需要的是“干净”观测值，这就需要将存储在计算机中的观测数据进行预处理。这个阶段主要包括数据格式转换、数据筛选和编辑、数据标准化、接收机钟差估算、线性组合观测值形成、基线向量近似值估算和周跳探测、修复等。

1.2 基线解算

基线解算采用美国麻省理工学院(MIT)和斯克里普斯海洋研究所(SIO)研制的GPS数据后处理和分析软件GAMIT，它是全球应用最广泛的高精度GPS基线解算软件之一，采用双差载波相位模型解算，多安装于Linux操作系统[3］。

1.3 GPS 网平差

GPS基线解算所得到的是基线向量，仅能确定点之间的相对坐标，要得到待定点的绝对坐标，就需要引入起算数据进行平差。GPS网平差的步骤分为以下几个:提取基线向量，构建GPS网;进行无约束网平差;约束平差或者联合平差;质量评定。本文中平差处理所用的软件为武汉大学的COSA软件。

2 GPS控制网优化设计的分类及指标

2.1 GPS控制网优化设计的分类

目前，广泛应用的GPS控制网优化设计由Grafarend E.提出，主要包括以下四类[4］:

零类优化设计是指在明确了网平差模型的系数矩阵和权阵的条件下，求解未知数协因数阵的过程。

一类优化设计是在全网观测点数和基线数大概确定之后，通过对网形的设计求出系数矩阵，以使得未知参数的协因数阵达到规定的精度要求。针对图形矩阵的设计，如下一些因素可能会对平差精度有影响:点位移动、异步环的数量和网平差中基线向量的选取等。

二类优化设计，是在已确定网形，即已知平差模型的系数阵和未知数协因数阵的基础上，对权阵进行优化设计的过程。

三类优化设计，是指对于精度没有达到要求的GPS网进行加密，使其逐渐满足精度要求的过程。

测量实践中，权阵和网形加密的情况不是很多，优化设计的主要工作集中在基准设计和网形设计这两部分内容。

2.2 GPS控制网优化设计的指标

GPS控制网优化设计的数学模型为:

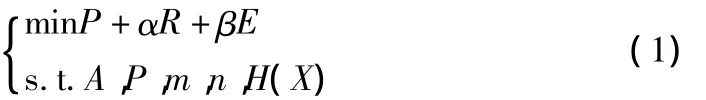
其中，P，R，E分别为精度、可靠性、经济指标;α，β均为常数，它们的不同取值可调节以上三个指标之间的比例关系;s.t.表示“约束于”，分别为图形矩阵和权矩阵;m，n分别为未知数的个数和观测值的个数;H(X)为限制条件函数。优化设计的目的就是通过调整改变约束条件中各因素的比例关系，即对网的各种参数(如基准、图形参数、观测权参数等)进行设计，使得目标函数得到极小值。

3 位置基准的分布对GPS网精度的影响

在进行平差之前，GPS网是一个自由网，要想获得待求参数的平差值，必须选取较高精度的点作为平差基准。对于大范围和高精度的GPS数据处理，起算基准的选择显得十分重要，通常都选择具有高精度的IGS地心坐标基准站。

图1 高纬度IGS基准站的GPS网形

下面通过实例来说明IGS基准站的分布对GPS网精度的影响。

设计两个简单的方案来分别说明高、低纬度基准站对GPS网精度的影响。选取中国境内的四个IGS站作为未知点，分别是CHAN，KUNM，LHAZ，SHAO。基准选取方案:方案一选取北半球的两个高纬度基准站，它们是IRKT(B=52°)，YSSK(B=47°);方案二选取北半球的两个低纬度基准站，它们是HYDE(B=17°)，GUAM(B=13°)。

相应网形图分别见图1，图2。

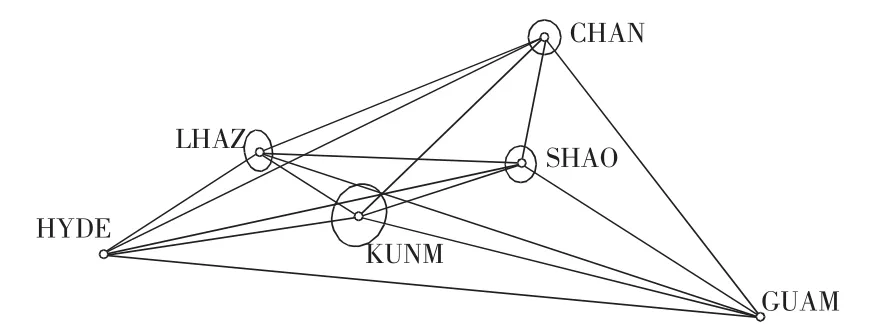
图2 低纬度IGS基准站的GPS网形

利用GAMIT软件进行基线解算之后，采用COSA软件分别将两组不同的基准站与中国境内的四个待求站 CHAN，KUNM，LHAZ，SHAO一起进行平差。解算结果显示:与方案一相比，方案二在X，Y坐标分量上的平均精度分别提高35.6%和34.6%，在Z坐标分量上的平均精度提高47.6%。由此可得:在所选IGS基准站个数相等的情况下，选择低纬度的基准站比选择高纬度基准站的精度在各个坐标方向都要高，尤其表现在Z坐标上。

4 结语

选择IGS站位置的不同，对GPS网精度的影响也不相同。在所选IGS站数量相同的时候，选择低纬度的IGS站与选择高纬度的IGS站相比，各个坐标轴的精度都有提高，尤其是Z轴。因此，在选择基准站时，最好是结合全球IGS站的地理分布状况，尽量选择低纬度的站点[5］。

[1]李 辉.高精度GPS控制网的优化设计研究[D］.北京:北京交通大学硕士论文，2009.

[2]李征航，黄劲松.GPS测量与数据处理[M］.武汉:武汉大学出版社，2005.

[3]刘志广，占 伟.Ubuntu系统平台的 GAMIT/GLONK10.35安装详解[J］.全球定位系统，2009(5):32-34.

[4]晁定波，薄志鹏.现代大地控制网优化设计原理[M］.武汉:武汉测绘科技大学出版社，1991.

[5]隋立芬，许其凤.GPS数据处理中IGS基准站的选取[J］.测绘学院学报，2003，20(1):124-126.