大跨度悬索桥索塔非线性稳定分析

张 琴

0 引言

随着现代桥梁向高墩大跨方向的发展，悬索桥型越来越受到重视，我国成功修建了虎门大桥(主跨888m)、润扬长江大桥(南汊桥主桥跨径布置为470m+1 490m+470m)和世界上最大跨度的钢箱梁悬索桥西候门大桥(主跨1 650m)，象征了我国桥梁建设水平进入国际先进行列。

索塔是悬索桥的主要承重构件，将由主缆传递下来的竖向荷载传至大地。随着跨径的不断增大，主塔高度的增加，主塔稳定分析成为控制悬索桥安全的主要因素之一。历史上曾经有过不少因桥梁失稳而丧失承载能力的事故[1］。结构失稳是指在外力作用下结构的平衡状态开始丧失稳定性，稍有扰动(实际上不可避免)则变形迅速增大，最后使结构遭到破坏。研究稳定理论就是要找出作用于结构内部抵抗力之间的不稳定平衡状态，即变形开始急剧增长的状态，从而设法避免进入该状态[2］，长久以来，许多学者为此进行了大量的研究和探索[3-7］。

本文针对某大跨度悬索桥主塔，采用大型通用有限元软件ANSYS，建立三维计算模型，分析了该桥主桥的弹性稳定性以及非线性稳定性。通过计算表明，大桥主塔的设计满足承载力要求，从而为类似桥梁的索塔稳定性分析提供借鉴。

1 计算原理

研究屈曲稳定问题常用的方法有静力法(Euler方法)、能量法(Timoshenko方法)、缺陷法和振动法。

1.1 线性稳定

对于一般构件，线性稳定问题可用静力平衡法，对于较复杂的结构，则采用有限单元法更适宜。分支点稳定分析假定结构失稳时处于弹性小变形的范围，结构的位移与外荷载成比例关系[8］，把结构的稳定分析转化为求特征值问题，得出的最小特征值即为失稳临界荷载，具体计算时可先用直接刚度法将各单元的则度矩阵(含几何刚度矩阵)集合成结构刚度矩阵，并建立结构的平衡方程:

其中，[K0］，[Kσ］分别为当前平衡状态下结构弹性刚度矩阵和初应力刚度矩阵;{d}为位移矩阵;{P}为外荷载，{P}=λ{P*}，λ为常数，{P*}为外荷载的相对值所组成的向量矩阵。

由式(1)得稳定问题的特征值方程为:

1.2 非线性稳定

含有初始缺陷和大位移结构稳定分析都属于非线性问题。缺陷法认为完善而无缺陷的理想中心受压直杆是不存在的。由于初始缺陷的影响，杆件开始受力时即产生弯曲变形，其值要视缺陷程度而定。在一般条件下缺陷总是很小，弯曲变形并不显著，只有荷载接近完善系统的临界值时，变形才增至很大，由此确定其失稳条件。初始缺陷和大位移问题可归结为求解一个非线性方程:

其中，[KL］为当前平衡状态下局部坐标系的大位移矩阵。在大位移稳定分析中，需要不断地计入几何非线性刚度矩阵，如果结构中的部分应力超过了材料的屈服强度时，还需计入材料非线性刚度矩阵。

由于结构在不断增加外荷载的作用下，其刚度矩阵不断地发生变化，当外荷载产生的压应力或剪应力使得结构切线刚度矩阵趋于奇异时，结构的承载力就达到了极限，此时的外荷载即为极限荷载。

2 算例

某大跨度悬索桥主跨为1 108m大跨度悬索桥，其桥塔从承台至塔顶高为195.276m，主缆横向中心间距为36.5m。桥塔的材料组成为C50钢筋混凝土。每条主缆给予桥塔塔顶处的竖向压力为16 000t，由大型有限元通用软件ANSYS10.0建立的三维梁系计算模型如图1所示，在计算模型中，只在塔底施加固结约束，采用Beam4单元模拟塔柱和横向联结系。

图1 桥塔计算模型

把由主缆传递给桥塔的竖向作用视为集中作用力，仅考虑主要由主缆传递的荷载作用时，通过计算得前六阶弹性稳定系数如表1所示。前四阶屈曲变形如图2～图5所示。

表1 弹性稳定系数 Hz

图2 一阶屈曲模态

图3 二阶屈曲模态

图4 三阶屈曲模态

图5 四阶屈曲模态

由表1和图2～图5的计算结果可知:第一阶弹性稳定系数为3.773，沿顺桥向屈曲，可以通过计算得到其极限承载力为60 373t。第二阶沿横桥向屈曲，稳定系数为10.187。

将特征值屈曲分析计算得到的第一阶屈曲模态的各节点的位移按0.01比例缩小，作为接下来计算模型的初始缺陷，同时施加略大于一阶屈曲模态的临界荷载，进行大变形非线性分析。通过计算，得到的荷载—位移(塔顶)曲线如图6所示。

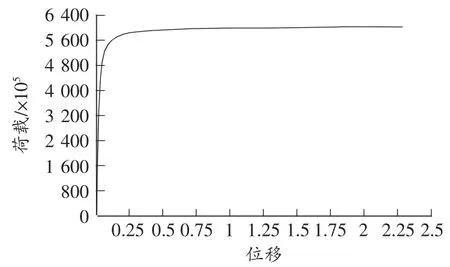
图6 荷载—位移曲线（一）

从图6中可以读得其临界承载力为54 000t左右，明显比前面计算的小。

在添加初始缺陷的基础上，再考虑20m高处百年一遇10min平均最大风速41.4m/s作用，按等效风荷载施加于梁单元上。通过计算，得荷载—位移(塔顶)曲线如图7所示，从图7中可以读得其临界承载力为43 000t左右。

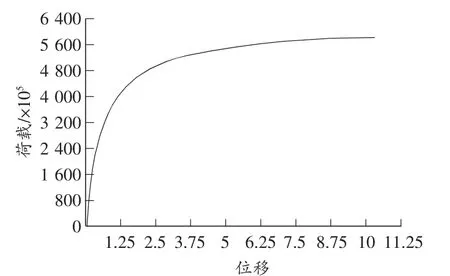
图7 荷载—位移曲线（二）

由上述计算结果不难看出，考虑材料缺陷和几何非线性后，其极限承载力明显比由直接特征值法所计算的小，添加横向风压等因素作用时，其极限承载力更小，但其安全系数均在2.69以上。

3 结语

通过采用有限元软件ANSYS10.0建立三维有限元计算模型，分析了几何非线性和材料非线性对某大跨度悬索桥主塔稳定性的影响。计算结果表明，几何非线性和材料缺陷对主塔的稳定性影响明显，考虑非线性的影响更能揭示稳定问题的实质，在实际大跨度桥梁稳定分析中，还应考虑风压、横向荷载等因素的影响。

[1]李国豪.桥梁结构稳定与振动(修订版)[M］.北京:中国铁道出版社，2003.

[2]Ye Yinghua，Diao Bo.Nonlinear analysis of concrete structures.HarBin Institute oftechnology Press，1996.

[3]Casas J.R.Reliability-based partial safety factors in cantilever construction of concrete bridges.Journal of Structural Engineering，1997，123(3):305-312.

[4]王振阳，徐 兴.高墩大跨径桥梁稳定性[J］.长安大学学报，2003，23(4):38-40.

[5]白 浩，杨 的，赵小星.高墩大跨径弯连续刚构桥梁空间非线性稳定分析[J］.公路交通科技，2005，22(5):111-113.

[6]张新培.钢筋混凝土抗震结构非线性分析[M］.北京:科学出版社，2003.

[7]Walter Dilger，Alaa Sherif.Stability of slender webs of prestressed concrete box-girder bridges.Journal of Bridge Engineering，2003，8(3):138-143.

[8]雷俊卿.大跨度桥梁结构理论与应用[M］.北京:清华大学出版社，2007.