基于模型跟踪的广义非线性控制系统设计方法

赵立华，大久保重范

(1.东北电力大学 机械工程学院，吉林 吉林132012;2.山形大学 工学部，日本山形992-8510)

模型跟踪控制(Model Following Control System，MFCS)是通过迫使被控对象跟踪具有理想动态特性和稳态品质的参考模型来获得期望的闭环系统性能的控制方法。在MFCS中，对目标信号没有特殊要求，一般信号即可满足控制器的设计要求，因此使得MFCS的应用非常广泛。MFCS的研究已经取得了一些研究成果，但基于广义非线性模型跟踪控制系(Nonlinear Descriptor Model Following Control System，NDMFCS)的研究成果还不多，本文对MFCS的设计进行扩展，提出了一种基于一般非线性模型的广义模型跟踪控制方法，并证明了系统内部有界。

1 问题的设定

由(1)、(2)式给出广义非线性控制系统

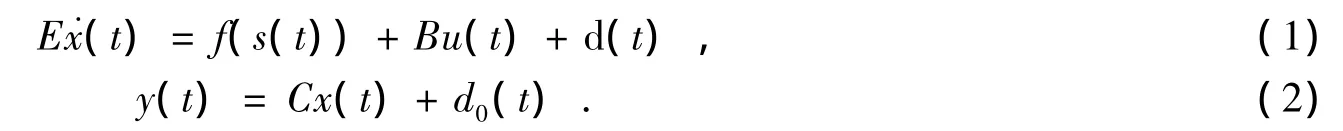
这里，E为正则矩阵，且满足rankE=r(r≤n);x(t)为广义变量，x(t)∈Rn;u(t)为控制系统的输入，u(t)∈Rl;y(t)为控制对象的输出，y(t)∈Rl;B，C为适当维数的常矩阵;f(x(t))为可利用的非线性变量，f(x(t))∈Rn;取d(t)∈Rl，d0(t)∈Rl为线性有界外界扰动，其特征多项式为Dd(p)，满足(3)式的数值多项式，模型由(4)式给出。

ym(t)∈Rl为模型的输出;rm(t)∈为参考模型输入;Dm(p)为稳定的对角多项式，满足。

Nm(p)为l×lm的多项式矩阵，各行的次数为∂rk{Nm(p)}=σmk。在此，∂{·}表示多项式{·}的次数，∂rk{·}表示多项式矩阵{·}第k行的次数。取对角矩阵可使问题研究简化，实际没有此限制;系统输出误差e(t)由(6)式表示。

本文讨论系统内部状态完全有界、输出误差e(t)渐进收缩于零的广义非线性模型跟踪控制系(NDMFCS)的设计问题。

2 控制系设计

取满足(7)式的，控制对象(1)可写成(8)式，K为适当维数的常矩阵。

本设计法与系统输入u(t)的初值无关，讨论对于闭回路状态方程式中的任意初值有界。令p=d/dt，控制对象的输入、输出关系可得

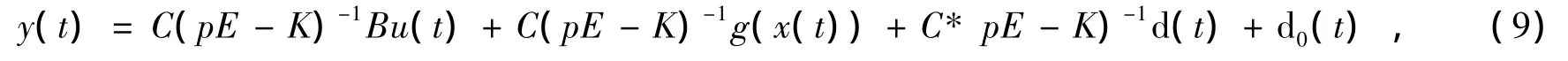
再由下面的(10)、(11)、(12)式:

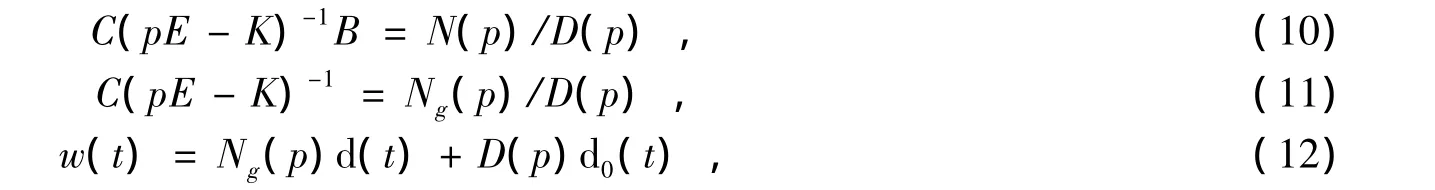
得到

取稳定对角矩阵T(p)=diagTk(p)。∂Tk(p)=ρk表示该对角矩阵第k行的次数，线性有界外界扰动特征多项式Dd(p)的系数为∂Dd(p)=nd，建立如下(14)条件式，适当取nmk值，使得ρk≥0。

使用上面的对角矩阵T(p)，求满足(15)式的S(p)。

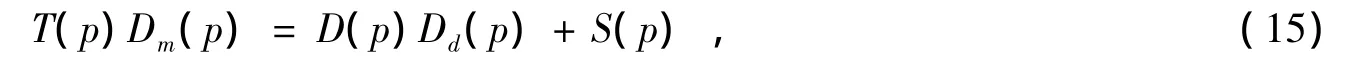
式中，T(p)，Dm(p)，D(p)为已知的多项式矩阵，Dd(p)为已知数值多项式。S(p)可由次数为nd的多项式对角矩阵求得。对于控制系统的输入u(t)，使用满足(16)式的稳定对角矩阵Q(p)，∂Qk(p)为角矩阵Q(p)第k行的次数。

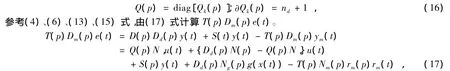
求使(17)式右侧趋近于零的控制系统输入u(t)的表达式，模型次数为nmk≥σmk。

(18)式的u(t)使(17)式的右侧等于零。

上式中T(p)，Dm(p)是稳定的多项式矩阵，所以得出

至此，如果构成控制系统的内部状态有界，便可实现模型跟踪控制系的设计。

3 内部状态有界的证明

使用状态空间将u(t)表示为

ζi(t)，(i=1～4)为以下状态空间函数:

多项式矩阵和系统矩阵的间有以下关系:

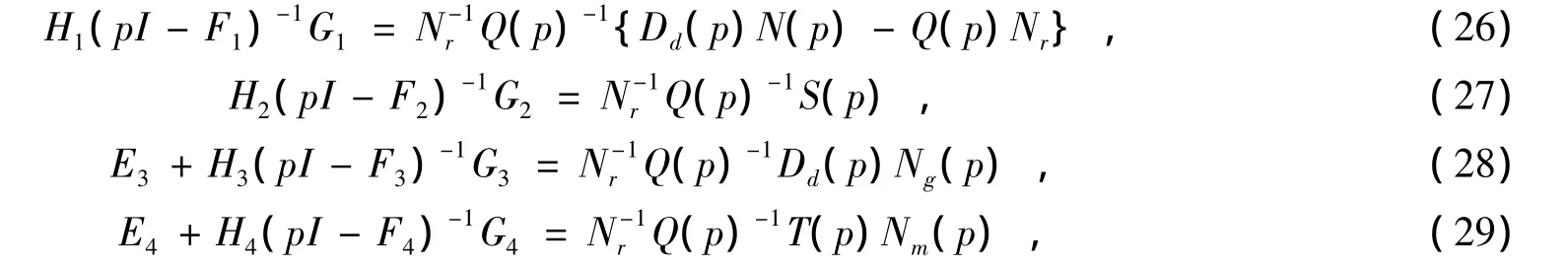
对于控制系来说，外部信号为模型的参考输入rm(t)和外界扰动d(t)、d0(t)，均为有界函数。为证明控制系内部状态有界，消去u(t)后，控制系可表示为如下的状态空间形式。

取向量z(t)如下:

则(31)式可写成

对比(31)和(34)式，可知 ～E，As，ds(t)，的内容。As的特征多项式，

由pI-Fi=Q(p)，(i=1～4)以及前面相关各式可得，

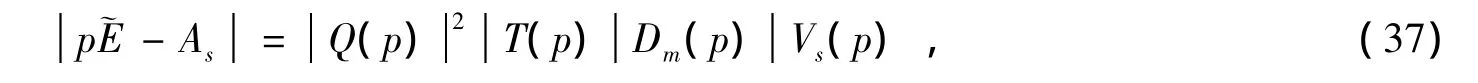
由(34)，(35)式，由g(x(t))至x(t)的传递特性可由下式描述。

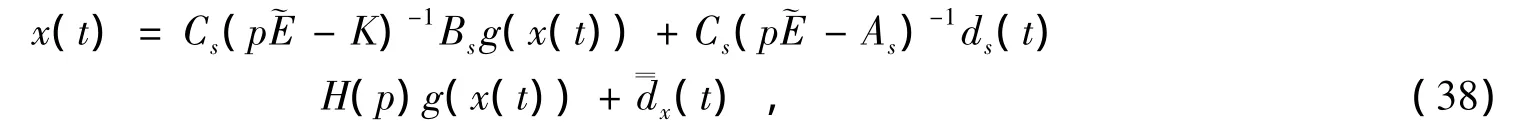
x(t)的有界性的证明可见下面的定理1。

定理1

所示控制系，如x(t)连续，且满足条件① ～④时，则x(t)有界。

限于篇幅，定理1的证明略［8］。x(t)满足定理1的条件，x(t)有界。由(34)式，x(t)有界，则g(x(t))有界;且ds(t)亦为有界函数，则内部状态函数z(t)有界，即控制系统内部有界。

4 结 论

本文在MFCS设计的基础上进行扩展，将控制对象分为线性和非线性两部分进行考虑，提出了一种内部有界的广义非线性模型跟踪控制系(NDMFCS)的设计方法，证明了当非线性部分满足给定范数条件、传递函数正实时，系统内部完全有界。

［1］池田雅夫.Descriptorシステムに基づくシステム理論［J］.計測と制御，1985，24(7):597-604.

［2］大久保重範.線形零点が不安定な場合の非線形モデル追従形制御［J］.計測自動制御学会論文集，1988，24(9):920-926.

［3］大久保重範.大域的に安定な多入出力非線形系のMRACS［J］.計測自動制御学会論文集，1990，26(1):46-53.

［4］大久保重範.零点の安定配置を使った非線形モデル追従形制御系［J］.計測自動制御学会論文集，1992，28(8):939-946.

［5］上里英輔，池田雅夫.ディスクリプタシステムに対する等式制約を含まないLMI安定条件とそのロバスト安定への応用［J］.計測自動制御学会論文集，1998，34(12):1854-1860.

［6］唐厚君，大久保重範.非線形ディスクリプタシステムのモデルモデル追従形制御系の設計［J］.電気学会論文誌，電学論C，2001，121(2):323-332.

［7］趙立華，大久保重範.不変零点の安定配置を使った非線形ディスクリプタシステムのモデル追従形制御系［J］.電気学会論文誌，電学論 C，2009，129(3):424 -431.