环形交叉口入口道车辆跟驰行为研究

金勇，刘岩

(1.大连市城市规划设计研究院 城市交通规划研究所，辽宁 大连 116011;2.大连交通大学 交通运输工程学院，辽宁 大连 116028;3.吉林大学 交通学院，吉林 长春 130022)

0 引言

环形交叉口具有很明显的主支路特征，当环内车流与进环车流相交时，环内车流有先行权，只有当环内的车流出现较大间隙时，进环的车辆才能进人交叉口.这也就意味着在环形交叉口入口道进入环形交叉口的车辆必须判断是否有足够的间隙插入.当车辆密度很大时，入口道的车辆必须减速，判断并等待“间隙”的出现.当前车的减速或制动行为影响到后车的运动状态时就发生了车辆跟驰现象.

环形交叉口是一种比较特殊的交叉形式，环形交叉口的设置形式、几何线形、交通组织方式和行人干扰等，都较其它形式交叉口特殊，因此环形交叉口入口道的跟驰行为应该不同于普通道路上的跟驰行为.本文通过基本的跟驰模型来研究环形交叉口入口道的车辆跟驰现象，从而探讨环形交叉口入口道车辆跟驰特点和运行状况等.

1 环形交叉口入口道跟驰模型研究

1.1 模型分析

目前，国内外已经建立了许多跟驰模型，比如线性模型，刺激—反应模型，安全距离模型，生理—心理模型，模糊推理模型，元胞自动机模型等［1］.其中，线性模型具有非常简便和对稳定性分析很敏感的优点，并且能够比较直观地反映车辆跟驰的一些特性，所以文章采用线性跟驰模型.

线性模型公式为［2］:

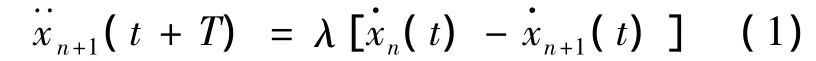
式(1)是在前后车间速度相等，制动距离相等，在反应时间内车辆的速度不变的三个假设条件下推导出来的.其中将λ认为是与驾驶员动作相关的系数，单位是1/s.该式表明后车的反应与前车的刺激成正比.

1.2 交通调查［3］

本文以大连市中山广场上海路入口道交通流为例，来分析环形交叉口入口道车辆跟驰状态.利用摄像法进行调查，沿车道横向贴上间距已知的标志线，并记录跟驰状态下前车(车1)和后车(车2)压到标志线的时刻，如图1所示.

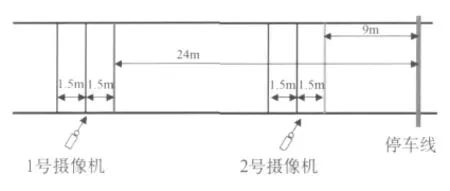
图1 调查方案示意图

研究车辆跟驰应该从车辆的基本运动状态出发，通过对车辆建立运动方程的方法来研究车辆的跟驰行为.因此，方案设计的目的也就是在于通过一系列的运动状态来拟合出车辆跟驰时运动状态的方程.本文以5 s作为判定跟驰行为的限界［4］，在读取数据时剔除掉车头时距大于5 s的数据，最终得到20组有效数据.

调查采集到的数据，首先得出散点图，接着拟和出位移—时间关系式，最后利用位移－时间关系式就可以得出环形交叉口入口道车辆跟驰状态模型，车辆时间—位移如图2所示.

我并不想为吕布的行为辩解。单就史料上看，他的确为利所动，杀了丁原、董卓，没什么好。只是，他真的比曹操、刘备等等，更恶吗？去读读《三国演义》，满目是狡诈、变节、阴谋、争战。所谓“老不看《三国》，少不读《水浒》”，因为年纪大点，经些世故，就能觉出，刘备之仁厚近乎伪，关张则近乎僭。

图2 车辆运动状态拟合图

拟合方程如表1所示，由于篇幅所限尽列3组关系式.

表1 车辆运动曲线拟合方程

2 参数标定

本节主要针对表1的拟合方程进行分析和处理.

根据运动学公式

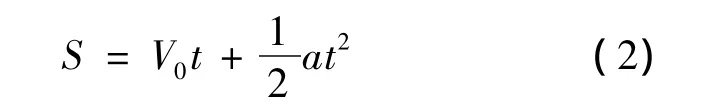
式(2)对t求导，得到车辆的加速度与速度之间的关系方程.

对表1进行对t求导得到表2.

利用前车压第一条线(即t=0时)的时刻来计算两车的速度差，对表2中的式子对t进行求导得到后车的加速度，经过计算得到需要标定的λ的值，如表3所示.

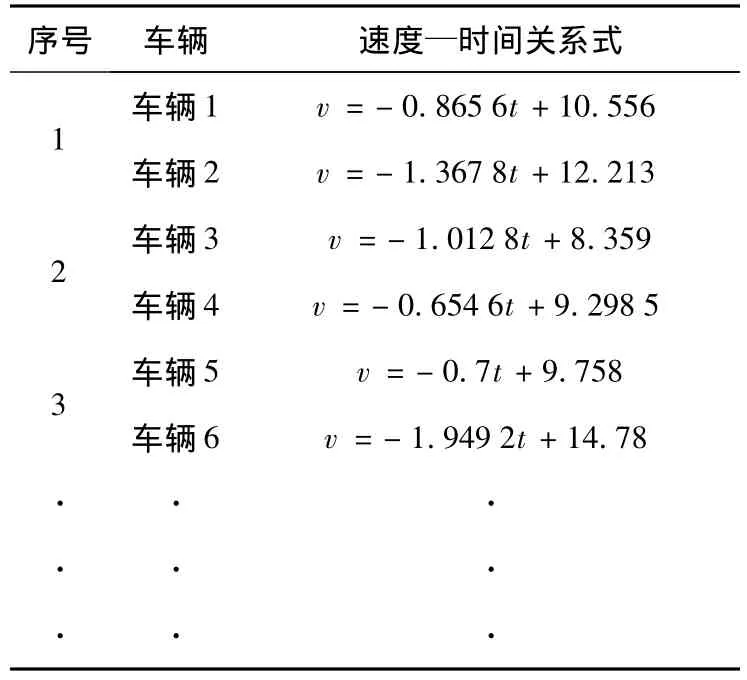
表2 车辆速度—时间关系式

表3 λ参数标定表(已经按n(t)－n+1(t)升序排序)

表3 λ参数标定表(已经按n(t)－n+1(t)升序排序)

序号时刻(T=1)前后车速度差x·n(t)－x·n+1(t)/(m·s－1)后车加速度x·n+1(t+T)m·s－2 标定λ的值 前后车距离差m 1 1.000 0 －7.799 0 －2.989 0 0.383 3 27.244 1 2 1.000 0 －7.593 2 －2.955 8 0.389 3 15.162 4 3 1.000 0 －7.554 0 －2.958 0 0.391 6 17.923 7 4 1.000 0 －7.554 0 －2.958 0 0.391 6 26.947 8

表3 λ参数标定表(已经按n(t)－n+1(t)升序排序)(续表)

表3 λ参数标定表(已经按n(t)－n+1(t)升序排序)(续表)

序号时刻(T=1)前后车速度差x·n(t)－x·n+1(t)/(m·s－1)后车加速度x·n+1(t+T)m·s－2 标定λ的值 前后车距离差m 5 1.000 0 －6.459 0 －1.473 2 0.228 1 39.971 1··················

3 车辆跟驰行为分析

3.1 车辆跟驰行为分析

通过对表3中得到的数据进行处理分析得到λ的分布图(图3)和前后车速度差和后车加速度分布图(图4):

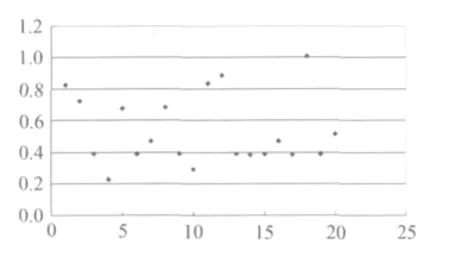
图3 λ值分布图

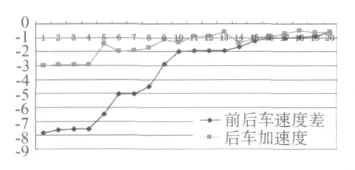
图4 前后车速度差和后车加速度分布图

(1)前后车速度差与后车的加速度有明显的相同走向，说明前后车速度差与后车加速度之间存在线性关系;

(2)后车的减速度与两车之间距离没有明显的关系;

(3)标定的参数λ的取值范围在0.2～1 s之间，λ值分布在0.4附近的概率最大，根据20组试验数据的统计分析，λ在数值0.39附近出现了8次，占了40%，因此推断λ的值应该在0.39左右波动.

3.2 线形模型稳定性的分析

在研究车辆跟驰时，车队中车辆的稳定性问题是很重要的.

所谓稳定有两层意思，一是指前后两辆车的距离是否稳定，例如车间距的摆动，若摆动大则不稳定，摆动小则稳定，这是局部稳定性;另一种是前车向后面各车传播速度的变化，如扩大其速度振幅则，则不稳定，如果振幅衰减，则稳定，称为渐进稳定性.

线形模型是一个复杂的二阶微分方程，利用拉普拉斯变换求解该方程并得到如下关系式:

式中，C为表示车间距摆动特性数值，该值越大表示车间距摆动越大，该值越小表示车间距的摆动趋近于零;λ为值越大，表示反应过分强烈;T为反应时间，s.

(1)表4列出了各种C值时车间距的摆动情况.可以看出，随C值的增加，车间距逐渐为不稳定.这是因为对出现的时间，反应时间越长，反应太强烈，则在做出反应时，情况可能偏离实际的需要.

表4 线形跟驰模型车间距摆动情况(π=3.14)

由此可见C=1.57是线性模型中车头间距从稳定到非稳定的临界值.一般情况下，正常人的反应时间约为T=0.8 s，以及表3所标定的参数λ 中代入式(4)，得到C 的值在0.182 48～0.806 27之间.根据表4判断，在中山广场环交入口道处车辆跟驰用线形模型分析时，车间距的摆动处于基本稳定和衰减摆动两种状态，这些表现是符合局部稳定性的.

(2)渐进稳定性.一列处于行驶状态的车队仅当C＜0.5时，才是渐进稳定的.与局部稳定性相比较，这里C=0.5时，车头间距的摆动衰减快.头车运行中的扰动是以的速率沿车队向后传播.当C＞0.5时，将以增大变动幅度传播，增大了车间干扰，当干扰幅度增加到使车间距小于一个车长时，则发生追尾事故.

4 结论

综上所述，可以看出车辆在环形交叉口入口道处表现出明显的跟驰现象.利用线性跟驰模型对跟驰进行研究时，可以看出反应强度系数的值在0.2～1.0之间，环形交叉口入口道的跟驰行为特殊于普通道路上的跟驰行为.

通过对数据进行分析，发现车辆跟驰时，后车的减速度受车间速度差的影响比较明显，但是受车间距的影响不明显，这点符合线性模型的观点.根据公式1计算出每个样本点的λ值，这些值在一定的范围内随机出现，其中λ值为0.38的值出现的概率比较大，占40%.

通过观察可以得知，环形交叉口车流密集时，车辆之间保持一个最小的车头时距t1，当车辆从入口道汇入环形交叉口时，前后跟驰车辆的车头时距为t2，只有当环形车流车头时距t＞t1+t2时，车辆才能进入.因此，从入口道车流的情况可以看出环形交叉口的运行状况.

［1］刘岩.车辆跟驰模型研究［D］.大连:大连交通大学，2006.

［2］王殿海.交通流理论［M］.北京:人民交通出版社，2002.

［3］刘岩，王殿海，韩萍.模拟弹簧车辆跟驰模型参数的标定［J］.大连交通大学学报，2011，32(1):17-21.

［4］何民，荣建，任福田.判定跟驰状态的研究［J］.公路交通科技，2001，18(4):74-78.

［5］陈斌，魏朗.高速公路意外事件影响下的车辆跟驰模型［J］.交通运输工程学报，2006，6(3):103-108.

［6］周商吾.交通工程［M］.上海:同济大学出版社，1987.

［7］章三乐，肖秋生，任福田.车辆跟驰理论的实用研究［J］.北京工业大学学报，1992，18(3):20-27.

［8］熊烈强，王富，李杰.考虑前后车速度关系的车辆跟驰模型［J］.华中科技大学学报(自然科学版)，2005，33(9):87-90.

［9］张智勇，荣建，任福田.跟车模型研究综述［J］.公路交通科技，2004，21(8):108-113.

［10］MARK BRACKSTONE，MIKE MCDONALD.Car-Following:A Historical Review［J］.Transportation Research，1999，2F(4):36-47.

［11］GAZIS D C，HERMAN R，ROTHERS W.Nonlinear Follow-the-Leader Models of Traffic flow［J］.Opns Res，1961，9:545-567.