相对变形约束下某离心机吊篮拓扑优化设计

陈 磊，洪建忠，杨永生，蒋春梅，李心耀

（中国工程物理研究院 总体工程研究所，绵阳 621900）

0 引言

目前，离心机被普遍应用于航天员超重训练、航天设备试验、仪器例行试验和岩土力学研究等方面。吊篮是联结试件与离心机转臂的纽带，它位于离心机最大加速度场中，其巨大离心力是离心机主要载荷之一。减轻质量、加强刚度、合理设计其结构外形可明显降低离心机的功耗，对提高离心机容量有重要意义[1]。

目前离心机吊篮设计通常采用经验结构，往往要经过反复设计和分析，直到结构强度、刚度满足设计要求。其效果好坏取决于设计者的经验。作为结构优化中的较高层次，拓扑优化技术能在更大程度上实现结构最佳功能和最小成本的结合，因此成为优化设计领域的热点。

本文基于HyperMesh/Optistruct平台，以吊篮质量为目标函数，以吊篮平台区最大变形为约束条件，采用变密度法对某离心机吊篮结构进行了拓扑优化设计，使其在保证吊篮平台最大变形的要求下实现轻量化目标，提高离心机的承载能力。

1 离心机吊篮设计要求

离心机在稳定运行时，吊篮受到空气阻力和试件与吊篮质量产生的惯性力作用。离心机在启动与制动过程中，由于吊篮的摆动还会产生随机的附加弯矩和摩擦力[2]。文中在极限工作条件下对吊篮进行优化设计，因随机产生的附加弯矩和摩擦力相对惯性力较小，可不予考虑：而空气阻力可以通过在吊篮迎风面前后加轻型整流罩予以有效降低。所以在吊篮设计及优化过程中，仅考虑模型和吊篮自身质量所产生的惯性力的影响[3]。

吊篮由吊臂、平台、销轴和轴承衬套组成。采用高强度的材料锻造加工而成的吊臂通过销轴与平台连接为一整体，其结构形式如图1所示。吊篮在离心场下运行时（如图2所示），吊篮平台与吊臂在C、D点采用销轴连接，吊臂在A、B点受到离心机销轴对轴承衬套的约束，同时，吊篮平台受到试件在离心场下所受离心力产生的载荷P和离心力G的作用。吊篮平台除了因吊臂的变形而整体沿离心力方向发生变形外，C和D两端将沿y向移动并发生弯曲变形。因此，定义C和D端的约束条件时，不能约束C和D端y向自由度与x向的旋转自由度[3-4]。

图1 离心机吊篮结构Fig.1 Structure of the centrifuge basket

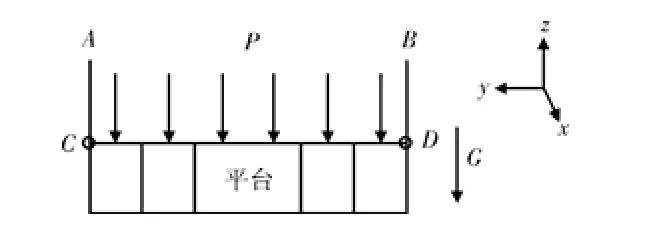
图2 吊篮平台约束及受力状态Fig.2 Constraints and forces on the basket platform

吊篮由几块34CrNiMo合金钢拼接而成，总质量为820 kg。经过有限元分析，吊篮最大等效应力发生在吊臂立柱，为174.5 MPa；吊篮沿离心力方向最大变形发生在吊篮平台中部，为0.51 mm。

为增加平台的刚度，保证试验的精度，通常平台是采用厚板与网格状的筋板焊接而成，在最大载荷作用下，吊篮平台变形量应控制在1 mm以内[2]。对于工作工况为200g的离心机，降低吊篮质量对销轴和转臂受力十分有利。显然，将吊篮轻量化作为设计目标比将吊篮刚度作为设计目标更加合理，因为在吊篮刚度满足指标要求的情况下，质量仍有优化空间。为满足离心机技术指标和设计要求，必须在控制吊篮平台变形量前提下，对吊篮进行优化设计，以实现吊篮轻量化要求。

2 离心机吊篮拓扑优化设计

2.1 拓扑优化基本原理

拓扑优化的最大优点是能在结构拓扑形状未定的情况下根据已知边界条件和载荷条件确定比较合理的结构形式，既能用于全新产品的概念设计，又能用于已有产品的改进设计[5]。优化设计有三要素：设计变量，目标函数和约束条件[6]。

优化设计的数学模型可表述为[7]：

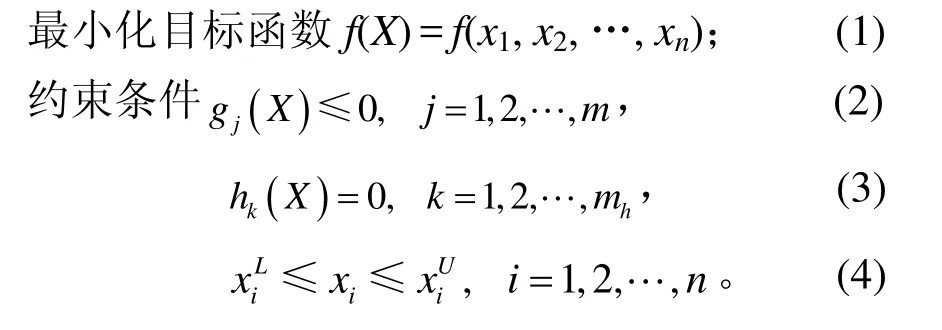
式(1)～(4)中：x=x1,x2, …,xn是设计变量，是在优化过程中进行改变以提高性能的参数；f(X)目标函数是优化所要求的最优设计性能，如体积最小、应变能最小；g(X)是不等式约束函数；h(X)是等式约束函数，是对设计的限制，如变形最大值。

本文采用HyperMesh/Optistruct软件的变密度法，假设结构由密度可变材料构成，此时设计变量x取为材料的伪密度，这样就将结构拓扑优化问题转化为单元材料最优分布问题。

结合离心机技术指标和设计要求，将离心机吊篮设计目标函数设为结构体积最小；将约束条件设为吊篮平台变形量不超过1 mm。

2.2 吊篮平台拓扑优化设计

如果采用整体拓扑优化，约束吊篮平台的变形量是比较困难的。为便于约束相对变形量，需对吊篮平台单独进行拓扑优化设计。

根据离心机吊篮外形最大尺寸及试验件安装空间等设计要求确定设计空间。如图3所示，将吊篮平台底部设为可设计区域，上部设为不可设计区域。吊篮吊臂上表面节点全部铰支，设定离心力场为200g，对吊篮平台上表面施加载荷，即300 kg试件在离心场下产生对吊篮平台1.15 MPa的均布压力载荷。

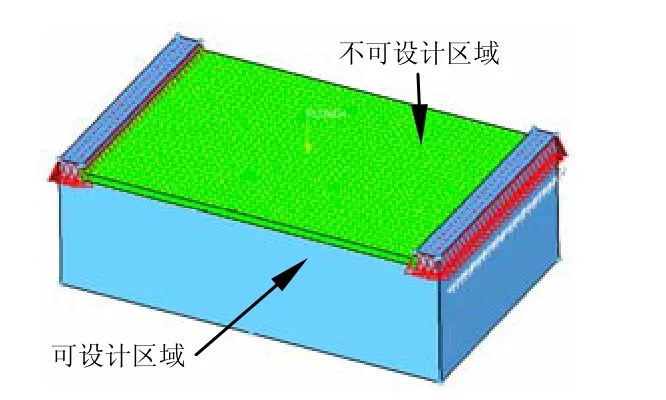
图3 吊篮平台设计空间Fig.3 The space for the design of the basket platform

变密度法拓扑优化后，会得出中间密度的材料，这与有材料或者无材料（即材料呈0、1分布）的实际设计情况不符合，因此要通过设定密度的阈值来消除中间密度材料[7]。为了在去除材料后获得结构比较清晰、材料分布比较连续的密度分布云图，通常将阈值取为0.1～0.3。将密度分布云图阈值设为 0.1时，吊篮平台拓扑优化的结果云图如图4所示。

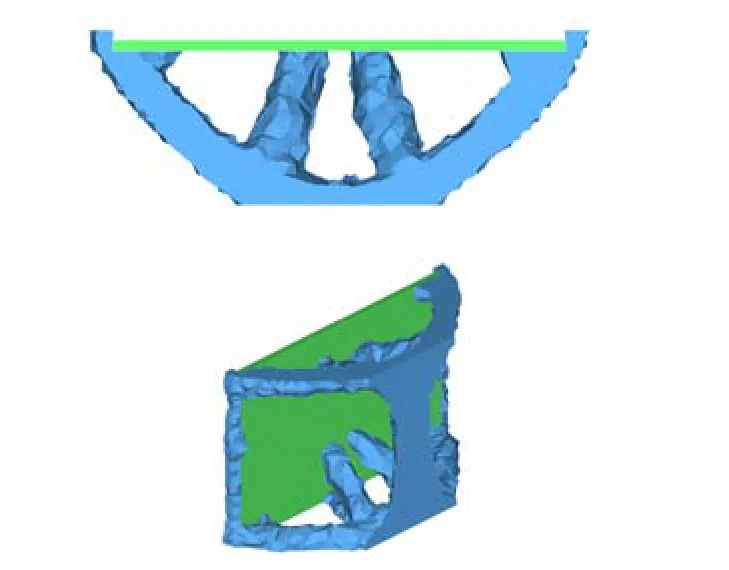
图4 吊篮平台拓扑优化结果云图Fig.4 Contour figure of the basket platform after topology optimization

拓扑优化分析的结果表明，设置如图4所示的加强筋板结构可以实现吊篮平台的最优材料分布。在实际的工程设计中，可以在此基础上进行进一步的结构参数优化设计，包括结构的尺寸优化和细节部位的形状优化等。

根据以上结论，参考离心机吊篮设计规范，设计出易加工制造的加强筋板结构吊篮。有限元分析表明，在与前述相同的载荷和边界条件下，吊篮最大等效应力为342.8 MPa，小于400 MPa的约束条件，对34CrNiMo合金钢来说安全系数大于2；最大变形量0.93，满足设计要求，此时吊篮平台质量为312 kg，如图5所示。

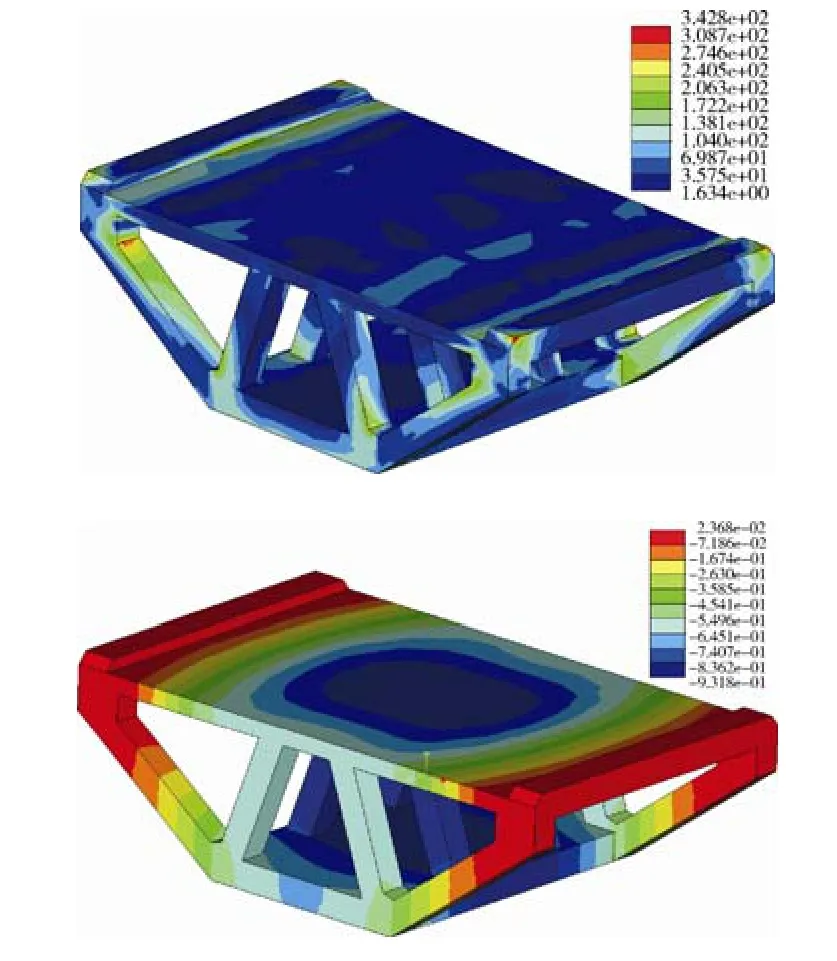
图5 吊篮平台的等效应力图和变形量图Fig.5 Stress contours and deformations of the basket platform

2.3 吊臂拓扑优化设计

同样对吊臂进行拓扑优化设计，以结构体积最小为设计目标函数，以最大等效应力小于400 MPa为约束条件，得到最优材料分布云图。应用尺寸优化思想，对优化后的吊臂结构进行有限元分析。轴承衬套内表面节点全部固支，设定整体离心场200g，对吊臂下表面施加载荷，即300 kg试件和312 kg吊篮平台在离心场下产生对吊臂17 MPa近似均布的拉力载荷。分析结果如图6所示，最大等效应力 365.9 MPa，小于 400 MPa，对 34CrNiMo合金钢来说安全系数大于2。此时吊臂质量93 kg，吊篮总质量为498 kg。

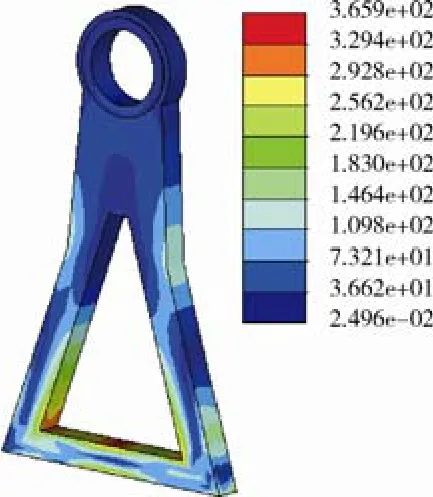
图6 吊臂有限元分析最大等效应力结果云图Fig.6 Stress contours on the basket’s arm from FEA

2.4 优化前后对比

为了考查吊篮结构拓扑优化效果，分别对拓扑优化设计前后的吊篮质量、最大变形量和最大等效应力进行对比分析，结果如表1所示。

表1 吊篮优化前后数据对比Table 1 Comparison of data between old and optimized baskets

从表1得出，经拓扑优化设计后，吊篮在最大变形量和最大等效应力满足设计要求的前提下，质量明显降低，降幅达39%，很好地实现了轻量化目标。

3 结束语

拓扑优化理论在结构设计中的应用尽管不是十分成熟，但我们可利用它给设计工作提供定性的理论指导。利用拓扑优化方法可以确定结构的密度分布云图，从而确定结构的基本形状；然后通过尺寸优化等方法对结构进行精确优化。

随着结构优化设计理论的不断成熟，拓扑优化方法将在工程设计中得到越来越广泛的应用。本文将拓扑优化理论应用于离心机吊篮的设计，实现了吊篮轻量化的目标，对提高离心机承载能力起到了重要作用。

（References）

[1]王东升, 刘青林, 钟继根, 等.某型号离心机吊篮拓扑优化设计[J].航天器环境工程, 2009, 26(3): 254-258

Wang Dongsheng, Liu Qinglin, Zhong Jigen, et al.The topology optimization design of a centrifuger nacelle[J].Spacecraft Environment Engineering, 2009, 26(3):254-258

[2]孙述祖.土工离心机设计综述[M].南京水利科学研究院土工研究所, 1990

[3]冉光斌, 罗昭宇, 刘小刚, 等.土工离心机吊篮的设计及优化方法[J].机械设计, 2009, 26(11): 68-70

Ran Guangbin, Luo Zhaoyu, Liu Xiaogang, et al.Design and optimization method of the suspended basket of geotechnical centrifuge[J].Journal of Machine Design,2009, 26(11): 68-70

[4]贾普照.稳态加速度模拟试验设备: 离心机设计（2）[J].航天器环境工程, 2009, 26(3): 186-200

Jia Puzhao.Steady state acceleration simulation test equipment: centrifuge design(Part 2)[J].Spacecraft Environment Engineering, 2009, 26(3): 186-200

[5]张胜兰, 郑东黎, 郝琪, 等.基于 Hyperworks的结构优化设计技术[M].北京: 中国机械工业出版社

[6]蒋丹杰, 邢立坤.基于有限元的某离轴三反系统支架的优化设计[J].科学技术与工程, 2010, 10(17):4153-4162

Jiang Danjie, Xing Likun.Optimizing a frame of off-axis three-mirrors anastigmat telescope based on FEM[J].Science Technology and Engineering, 2010, 10(17):4153-4162

[7]邢立坤, 孙丽崴.基于 HyperWorks/OptiStruct的辐射制冷支撑结构拓扑优化设计[J].科学技术与工程,2010, 10(11): 2803-3806

Xing Likun, Sun Liwei.Structure topology optimization design of radiation cooling support structure based on HyperWorks/OptiStruct[J].Science Technology and Engineering, 2010, 10(11): 2803-3806