混合群智能算法在模体识别中的应用

杨 柳，刘铁英，李雪莲

（1.吉林工商学院 信息工程分院，长春 130062；2.长春职业技术学院 信息分院，长春 130033；3.吉林省财政厅 吉林省财税信息中心，长春 130021）

混合群智能算法在模体识别中的应用

杨 柳1，刘铁英2，李雪莲3

（1.吉林工商学院 信息工程分院，长春 130062；2.长春职业技术学院 信息分院，长春 130033；3.吉林省财政厅 吉林省财税信息中心，长春 130021）

为了避免传统吉布斯算法的诸多缺陷，提高算法的求解能力，对蚁群算法（ACO：Ant Colony Optimization）进行了改进：引入粒子群算法（PSO：Particle Swarm Optimization）动态调节ACO函数中的参数获得最优解。在奔腾PC机的实验平台上、Windows 2003Server操作系统下、开发工具为VB的模拟实验中，结果证明，混合的群智能算法使经典旅行商问题求解的计算时间缩短，提高了算法的收敛速度，有较好的发展前景。利用PSO处理连续优化问题的优点，将混合算法应用于生物信息学的模体识别中，可实现更加快速的基序发现处理。

吉布斯算法；粒子群算法；模体识别

0 引 言

传统的蚁群算法［1，2］在离散问题上取得了很好的研究结果，但有几个突出问题制约了算法的应用。其中重要的一点是，蚁群算法的参数繁多，设置参数时根据人工经验进行，所以对不同问题，蚁群算法的参数都需要进行改变，而且参数选择往往对算法的结果有至关重要的影响。通常，同一问题，用同样算法，由于参数设置的不同，结果大相径庭。一个完善的算法不仅要有稳定的适应性，还要有输出结果的一致性。现将具有全局优化功能的群智能算法粒子群优化算法（PSO：Particle Swarm Optimization）［3，4］应用于蚁群算法（ACO：Ant Colony Optimization）模型中，对参数进行自动选择，通过PSO自动调节参数的功能，使参数选择不再依赖于人工经验，而且在特定的组合优化经典旅行商（TSP：Traveling Salesman Problem）问题中，这种混合算法都能得到比较满意的结果。

在生物信息学问题上智能算法已经取得很多成果，如，仿生类进化算法，人工神经网络［5］等。为提高传统方法求解能力，笔者设计了一种通过粒子群算法自动调节蚁群算法主要参数的混合算法，使在解决TSP问题上得到较满意应用结果的前提下，将混合的群智能算法应用于生物信息学中的模体识别问题，实验结果证明混合的群智能算法避免吉布斯方法的冗余解，有效减少了算法的运行时间，取得了较好的结果。

1 PSO／ACO混和算法

群智能算法作为一种新兴的演化计算技术，如同模拟进化算法，是通过群体中个体的有效解组成群体进化迭代实现寻求最优解的过程［1－4］。

概率选择是蚁群算法的主要思想，选择参数设置要依赖于实验人员经验设置。如果选择的不合适，将使结果不理想。同是群智能算法的粒子群算法在连续问题上得到了很好的结果［6，7］，所以，将PSO算法用于ACO算法参数的自适应调节以解决TSP问题的目标函数

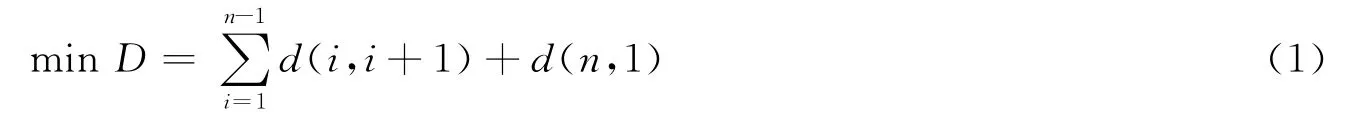
其中d（i，j）（i，j＝1，2，3，…，n）表示城市i与j之间的距离。

ACO在选路中的概率函数

其中ηij为距离因子，τij（t）为边弧（i，j）信息素的强度，α表示信息素在选择概率上的作用率；β是指路径长度在选择概率上的作用率。参数α与β对解的影响很大，为了选择最优参数，引入PSO算法。

PSO算法的计算如下

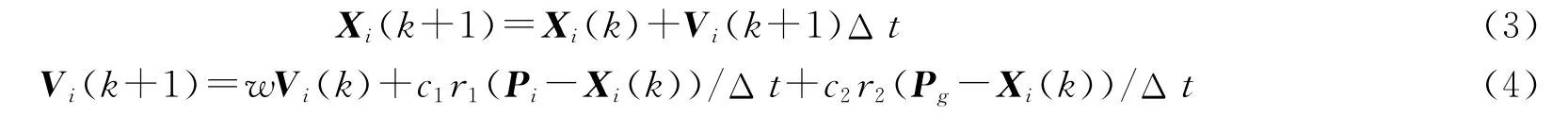
其中k为迭代次数，Vi为速度向量，Δt为时间间隔，Xi为第i个粒子的位置向量，c1和c2是非负常数，r1和r2是介于［0，1］的随机数，w是惯性权重，随着迭代的进行线性地减小［7］。

应用PSO自动调节ACO中的参数：粒子被定义在一个范围中，将每个粒子的位置定义为一个潜在的解，粒子群根据式（3）进行位置变换，由式（3），式（4）中第i个粒子的位置向量Xi，第i个速度向量V，自动优化配置ACO中的主要参数α和β能使算法收敛，在奔腾PC机、操作系统为Windows 2003Server、开发工具为VB的的实验平台上进行TSP模拟实验，优化参数α和β后重新带入式（2）中，在目标函数中以St70，Att48作为ACO运算取值，计算概率函数，与单纯ACO算法的概率函数运算时间和最优解的对比结果如表1所示。

表1 PSO／ACO算法与ACO算法对比Tab.1 PSO／ACO and ACO algorithm comparion

从混合算法的实验结果可以看出，在不同条件下，自适应地对参数进行调节，改进算法较基本蚁群算法在运行速度和解的质量上都有较明显提高，说明改进有效。

2 生物信息学中的模体识别问题

生物信息学中的模体识别问题是揭示核酸和蛋白质序列的生物意义的基本方法［8］。问题的关键是找到不同序列间的相似段落，类似数据结构中的字符串匹配，是一种近似的方法求解模体，不必严格匹配。其中人们将具有某种特征模式的序列片段称为模体，为了区分模体在核酸序列中的不同，通常在蛋白质序列中叫模体，而在核酸序列中叫基序。在用计算机进行模体识别问题的处理时，基序的发现主要有两种描述的方法：1）确定性的描述方法，但对海量数据是不能现实的；2）基于模糊查找方式，基于统计方法实现。统计方法主要有吉布斯采样方法、Meme方法和Consensus方法。3种方法的共同特点是用统计思想设计算法，并实现对给定目标的优化。

目前，最多使用的方法是吉布斯方法［9］。其主要步骤如下。

第一步 初始化。生成任意n在各条序列中的起始位点，可以记为M＝｛Mi｝，i＝1，…，n。建立位置频率矩阵Q。建立调控元件模型与背景模型。

第二步 更新。为了描述非模体区域的情况，需要建立背景模型。根据变化后的结果来计算位置频率矩阵。

第三步 采样。根据轮盘赌原理选择新的候选调控元件，计算出两种得分的比值，以较大的概率选取比值较高的候选调控元件，使其起始位点加入到M中。如果大于前一次得分，则转到第二步，继续迭代；否则，重复第三步，直到重复次数大于一个预设定值。如果所有序列都处理完，则转第四步；否则，转第二步。

第四步 结束。

3 混和算法在模体识别中的应用

因为吉布斯方法在模体识别中取得了很好的应用结果，所以在很多情况下，实践应用的方法都是在传统的吉布斯抽样方法基础上进行改进的。传统的吉布斯抽样方法［10］主要有两个明显缺陷：1）在每个序列中都要选择位置，虽然对于大规模的海量数据而言，以牺牲准确率获取速度，在一定范围内是准许的，但将很大程度地降低算法的执行效率；2）由于要对计算的每个起始位置进行打分，而很多打分是没有任何意义的，只有采用优化算法，提高算法的运算速度，才能更好地解决问题。

改进的步骤如下。

1）对一个找到的基序，对其中每个变量进行迭代采样。迭代后，吉布斯采样最终得到一个平稳分布。准确度打分函数如下

其中pik＝Q（i，ak），ak为A＝｛a1，…，aL｝中第k个字母，q为背景模型顺序取值。应用式（5）对子串进行打分。

2）在输入序列找到一个基序的标本。利用混合群智能算法在待查序列中找到一系列的最优候选位置。概率计算如下

其中pk（li）表示蚂蚁k在位置l选择字符i的概率，α是信息素的影响因子，S是输入的序列。τli（t）定义如下

3）对信息素的值进行更新后，由于在Ai中候选位置的数量取决于参数θ（θ为序列（1，2，4，16，64，…，n）的自选值），找到ni／θ个候选位置用来构造Ai，对于每个候选位置，用式（5）计算打分，当基序的候选子集变化时，退出程序。由得分函数（4）计算改进后与原始吉布斯算法的运算时间与准确度打分对比实验结果如表2所示。

实验结果表明，由于混合群智能算法决定吉布斯采样过程的候选序列，候选序列的大小取决于参数θ，θ越大，候选序列越小。随着候选集规模的下降，虽然算法的执行效率得到很大提高，但打分也随之降低，从而影响了混合算法的精确度，但该精确度是在可接受范围内的。

改进的混合算法提供了一种新型的可用于连续优化问题处理的方法。该方法扩大了参数选择的范围，更有利于算法找到最优解。实验结果证明了群智能算法在该领域有很好的应用。

表2 混合算法与传统吉布斯方法的比较Tab.2 Hybrid algorithm and Gibbs method comparison

4 结 语

笔者通过粒子群算法自动调节蚁群算法主要参数的混合算法，用于生物信息学中的模体识别问题，扩大了参数选择的范围，更有利于算法找到最优解。模体识别问题本身适合于混合算法的数据模型，首先，应用PSO／ACO混和算法在待查序列中找到一系列的最优候选位置；然后，应用吉布斯抽样方法对找到的候选解中有用的候选解计算分值。模拟实验表明，混合群智能算法较之传统的吉布斯方法运算效率得到很大的提高，而且对于海量数据，牺牲准确率换取速度的方法在一定范围内是被准许的。所以，可以减少计算时间，从而提高了算法的效率，代价是牺牲了一定的稳定性。PSO／ACO混和算法对大量模体特征的识别具有非常显著的优势，提高了序列分类的准确性。模体识别的实验亦可证明群智能算法在该应用领域中有很好的前景和较大的影响力。在今后的研究中还需进一步提高自动调控的准确度和稳定性，使群智能混合算法为各应用领域的实际工程问题提供更好的解决方法。

［1］DORIGO M，MANIEZZO V，COLORNI A.The Ant System：Optimization by a Colony of Cooperating Agents［J］.IEEE Transactions on SMC，1996，26（1）：1-13.

［2］DORIGO M，GAMBARDELLA L M.Ant Colony System：A Cooperative Learning Approach to the Traveling Salesman Problem［J］.IEEE Transactions on Evolutional Comutation，1997，1（1）：53-66.

［3］王凌.智能优化算法及其应用［M］.北京：清华大学出版社，2001.

WANG Ling.Swarm Intelligence Algorithm and Its Application［M］.Beijing：Tsinghua University Press，2001.

［4］KCNNCDY J，EBERHART R C.Particle Swarm Optimization［C］∥Proc the IEEE International Joint Conference on Neural Networks.Orland，USA：［s.n.］，1995：588-590.

［5］林和平，张秉正，乔幸娟.回归分析人工神经网络［J］.吉林大学学报：信息科学版，2010，28（2）：147-149.

LIN He-ping，ZHANG Bing-zheng，QIAO Xing－juan.Regression Analysis Artificial Neural Network［J］.Journal of Jilin University：Information Science Edition，2010，28（2）：147-149.

［6］EBERHART R C，KENNEDY J.A New Optimizer Using Particle Swarm Theory［C］∥Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Nagoya，Japan：［s.n.］，1995：39-43.

［7］LI Yan-jun，WU Tie-jun.A Nested Hybrid Ant Colony Algorithm for Hybrid Production Scheduling Problems［J］.Acta Auomatica Sinica，2003，29（1）：95-101.

［8］KEICH U，PEVZNER P A.Finding Motisf in the Twilight Zone［J］.Bioinofrmatics，2002，18（10）：1374-1381.

［9］THOMPSON W，ROUCHKA E C，LWARENCE C E.Gibbs Recursive Sampler：Finding Transcription Factor Binding Sites［J］.Nucleic Acids Research，2003，31（13）：3580-3585.

［10］NEUWALD A F，LIU J S，LWARENCE C E.Gibbs Motif Sampling：Detection of Bacterial Outer Membrane Repeats［J］.Protein Science，1995，4（8）：1618-1632.

Application of Hybrid Swarm Intelligence Alogrithm on Finding Motif Problem

YANG Liu1，LIU Tie-ying2，LI Xue-lian3

（1.Department of Information Engineering，Jilin Business and Technology College，Changchun 130062，China；2.School of Information Technology，Changchun Vocational Institute of Technology，Changchun 130033，China；3.Jilin Taxation Information Center，Jilin Provincial Finance Department，Changchun 130021，China）

In order to avoid many Gibbs algorithm defects，improve the ability of problem solving，improvements the ACO （Ant Colony Optimization）：PSO （Particle Swarm Optimization）is made to optimize the parameters in the ACO.Pentium PC machine is the experiment platform，operating system is Windows 2003Server，development tools is VB，the traveling salesman problem is tsimalated.Results show that the computing time of the algorithm can be reduced by new methods.It had great effects in practicality and rapid processing of motif discovary.

Gibbs algorithn；particle swarm optimization；finding motif

TP313

A

1671-5896（2012）01-0056-04

2011-09-01

吉林省教育厅“十二五”科学技术研究基金资助项目（吉教科合字［2012］第371号）

杨柳 （1979—），女，长春人，吉林工商学院讲师，硕士，主要从事智能算法研究，（Tel）86-15584279857（E-mail）yangliu7025＠sina.com。

（责任编辑：何桂华）