气液界面传质过程Rayleigh对流模拟的格子Boltzmann方法

付 博，袁希钢，陈淑勇，刘伯潭，余国琮

气液界面传质过程Rayleigh对流模拟的格子Boltzmann方法

付 博，袁希钢，陈淑勇，刘伯潭，余国琮

(天津大学化工学院化学工程联合国家重点实验室，天津 300072)

浓度梯度导致的Rayleigh对流是一种通常在传质过程中观察到的界面现象．为了模拟乙醇吸收CO2气液传质过程中界面传质引发的Rayleigh对流现象，提出了描述界面扰动的随机扰动模型，并建立了带有双分布模型的二维格子Boltzmann方法(LBM)．模拟二维液相Rayleigh对流过程中，假设界面上CO2浓度为常数．通过模拟研究，确定了随机扰动模型的2个参数：局部扰动概率P和浓度扰动大小ρD．模拟结果表明，当0＜ρD≤10-9,kg/m3、10-6≤P≤10-1时，平均液相传质系数存在一个稳定值：(1.09±0.02)×10-5,m/s．通过考察浓度分布结构，分析了Rayleigh对流的时空演化过程．根据模拟结果定义并计算了传质增强因子，其证明了Rayleigh对流能够有效地强化界面传质．

Rayleigh对流；格子Boltzmann方法；界面传质；液相传质系数；传质增强因子

在相际传质过程中，由物质在相界面上的传递而导致的浓度梯度会产生密度梯度，若密度梯度与重力作用方向相反，则称之为界面Rayleigh不稳定．此时若遇扰动，则会出现界面失稳进而引发的界面流体流动现象，称之为Rayleigh对流．Rayleigh对流的发生对界面传质有显著影响[1]，因而，研究Rayleigh对流对精馏、吸收等化工过程具有重要的意义．以往的实验研究和理论研究主要集中在采用光学测试手段如投影法、纹影法、激光全息干涉法等观察Rayleigh对流结构[2-4]、Rayleigh对流开始的不稳定性分析[5-6]、传质速率的测量[7]以及传质系数关联式的建立[8]．其中实验研究只能得到传质过程的宏观信息，而不能得到界面传质的微观信息；理论研究虽然能够预测传质过程中Rayleigh对流发生时的临界点，但不能给出Rayleigh对流发生后的具体传质信息．因此，有必要对Rayleigh对流发生后详细的流动及传质情况进行研究．随着计算机技术的发展，数值模拟为更好地考察Rayleigh对流及其在强化界面传质中的作用提供了更多可能性，研究结果将有助于了解Rayleigh对流强化界面传质的机理．格子Boltzmann方法(lattice Boltzmann method，LBM)作为一种新兴的数值计算方法，由于其在介观尺度上具有物理条件清晰、边界处理容易实现、计算效率和数值精度高等优势，已经被成功地应用于Rayleigh对流的数值模拟中．在气液传质过程中，以往针对液相Rayleigh对流的格子Boltzmann模拟通常假设界面存在一个或多个始终存在、位置固定并且浓度恒定的高浓度区域[9-10]．但是，在真实界面传质过程中，界面Rayleigh不稳定失稳引发的Rayleigh对流是复杂的，界面会出现来自各个方面的随机扰动，如局部浓度不均匀、物理震动甚至界面的分子热运动等．因此有必要提出一个求解真实界面传质过程中Rayleigh对流的格子Boltzmann方法．

笔者首先引入一种随机扰动模型来描述界面浓度扰动过程，以乙醇吸收CO2界面传质为对象，采用带有双分布模型的格子Boltzmann方法模拟液相中二维非稳态Rayleigh对流过程．通过模拟，分析和计算了不同模型参数下Rayleigh对流的特征：液相传质系数和浓度分布，通过传质增强因子考察了Rayleigh对流对界面传质的影响．

1 用于Rayleigh对流模拟的格子Boltzmann方法

1.1 双分布模型

本文采用双分布模型[11]建立了界面传质引发Rayleigh对流现象模拟的格子Boltzmann方法．该模型假设双组分流体由溶剂A和溶质B组成，且B的含量远小于A．双分布模型包含2个粒子分布函数fAi和gBi，分别用于求解流场和浓度场．无外力项时，基于如图1所示D2Q9格子模型[12]，则溶剂和溶质的LBGK演化方程[13]为

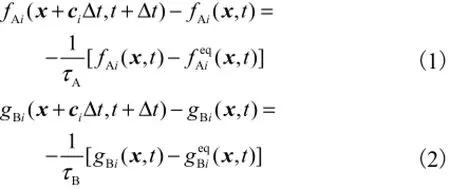
式中：ci为离散速度，m/s；i为基于D2Q9模型的粒子运动方向，i=1，··，9；Δt为单位时间步长，s；τ为无因次松弛时间；fAi(x，t)和gBi(x，t)分别表示t时刻在x位置沿着i方向的溶剂A和溶质B的粒子分布函数．

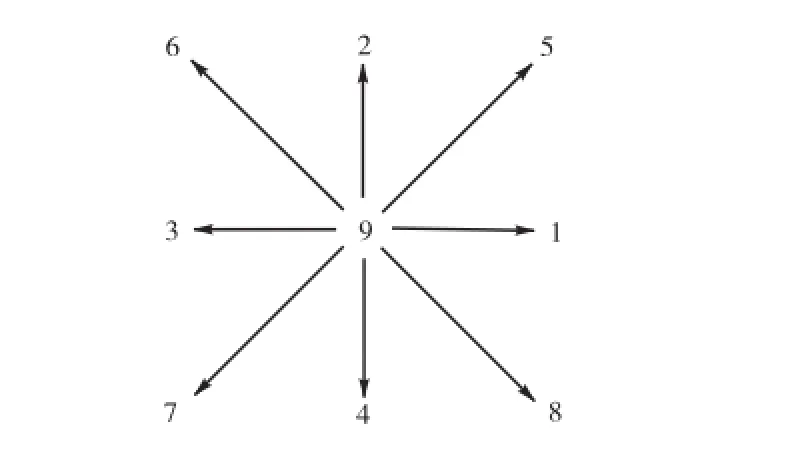
图1 二维九速模型(D2Q9模型)Fig.1 Two-dimensional nine-velocity model(D2Q9,model)

溶剂A和溶质B的平衡分布函数[11]为

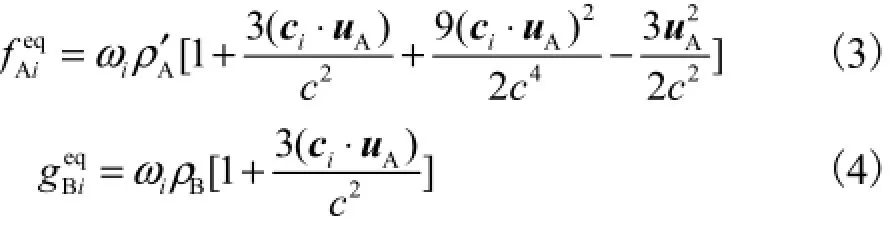
式中：c为格子速度，c=Δx/Δt，一般取为1；Δx为单位网格步长，m；uA为宏观速度，m/s；ρ′A为宏观密度，kg/m3；ρB为溶液中溶质的浓度，kg/m3；ωi为权重系数，ω1=ω2=ω3=ω4=1/9，ω5=ω6=ω7=ω8= 1/36，ω9=4/9．

通过粒子分布函数可以计算流场的宏观变量(密度、速度和浓度)，即

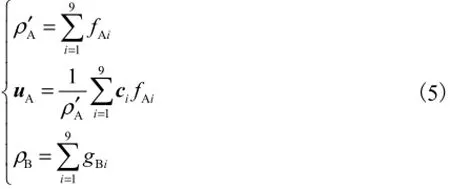
液体的黏度和溶质在溶剂中的扩散系数表达式[11]为

式中：ν为液体的运动黏度，m2/s；D为溶质在溶剂中的扩散系数，m2/s．

1.2 外力处理

本文引入Boussinesq近似[14]，即假设除密度外流场的其他物性(扩散系数、黏度等)为常数，因而体系所受的外力仅考虑密度变化导致的体积力．本文假设流体密度是浓度的线性函数，因此传质导致的浓度的变化是流体所受外部力(即重力)的唯一来源．类似于温度梯度导致的Rayleigh-Bénard对流中体积力处理方法[14]，则Rayleigh对流中体积力可近似表示为

式中：F为Rayleigh对流中单位体积的体积力，N/m3；g为重力加速度，m/s2；ρ0为溶液的初始浓度，kg/m3；Δρ′为纯溶剂与饱和溶液之间的密度差，kg/m3；ΔρB为纯溶质与饱和溶液之间的浓度差，kg/m3．

通过修正平衡分布函数中的变量速度uA来体现外力F对流体的影响．则平衡分布函数中的速度和流场速度将分别被修正为u*和u[15]，即

1.3 边界处理

对于流场和浓度场，左右边界均采用周期边界；下边界均采用反弹边界．对于上边界，浓度场采用恒浓度边界[16]；流场采用镜面对称边界[17]．其中镜面对称边界用于处理无变形气液自由界面时能够保证水平速度沿竖直方向上的梯度为0，考虑流场被均匀网格覆盖，其具体做法是假设上边界外还有一层虚拟结点，令虚拟结点的分布函数与上边界结点的分布函数沿二者的中心线对称相等．

1.4 随机扰动模型

在界面Rayleigh不稳定条件下，一旦有界面扰动，界面会产生Rayleigh对流．界面扰动可能是任何随机事件，如机械振动、分子的热运动导致的局部浓度扰动等，因而具有随机特征．对于在静止气液接触系统的等温传质过程，可以认为扰动仅仅为浓度扰动．因此这里提出了基于浓度扰动的随机扰动模型来模型化界面扰动过程，该模型采用2个参数描述其随机特征：局部扰动概率P表示液相界面上每个结点出现浓度扰动的概率；因扰动导致的浓度净增量ρD，即浓度扰动大小(设ρD远小于界面浓度ρI)．在LBM模拟中液相界面上每个结点的浓度0Ιρ表达式为

式中Βρδ为浓度扰动增量．计算中每个结点均产生一个随机数，如果该随机数小于P，则Βρδ=±ρD，否则δρΒ=0，且δρΒ的时均值为0．

2 Rayleigh对流的LBM模拟与分析

模拟对象为乙醇溶液吸收CO2过程中，由于CO2通过界面向液体乙醇中扩散所导致的Rayleigh对流现象．二维计算区域如图2所示，为静止的液体乙醇，其高为H、宽为L，传质开始前液相为纯乙醇．计算区域的上边界为气液自由界面，CO2通过上边界进入液相，下边界为可视为刚性边壁．乙醇吸收二氧化碳的气液传质过程是Rayleigh不稳定的和Marangoni稳定的[4]．

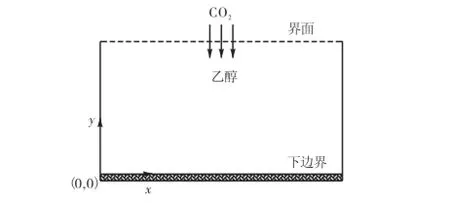
图2 Rayleigh对流计算区域示意Fig.2 Computational domain of Rayleigh convection

模拟基于以下2个假设：①液膜控制传质过程，界面上气液两相达到平衡状态，即界面浓度ρI可视为恒定值[18]，取为4.70,kg/m3；②忽略气液传质过程中的热效应，且自由界面没有变形．模拟初始条件：液相主体中各结点速度均为零，CO2浓度为零．取单位网格步长为5×10-5,m，此时可以获得可接受的准确结果．其中在298.15,K、101.325,kPa条件下，纯乙醇及其饱和CO2溶液物性[4,19-20]见表1．表中：0ρ′为纯乙醇密度；Bρ∗为界面平衡浓度；μ0为纯乙醇的动力黏度.

表1 在298.15,K、101.325,kPa条件下纯乙醇及其饱和二氧化碳溶液物性Tab.1 Physical properties of ethanol and CO2saturated solution at 298.15,K and 101.325,kPa

2.1 模型参数的确定

传质系数是反映传质能力的重要基础数据，可以通过考察模型参数对传质系数的影响来确定P和ρD的合适取值区间．取计算区域高H=5,mm、宽L= 5,mm，网格划分为100×100．

t时间内平均液相传质系数kavg,t(m/s)可表示为

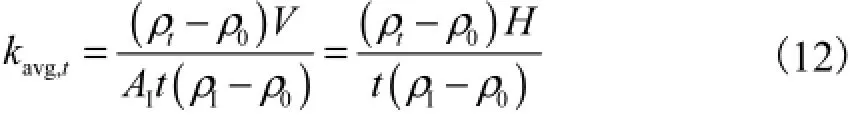
式中：V为溶液体积，m3；AI为界面面积，m2；ρt为t时刻溶液中溶质的平均浓度，kg/m3．

图3给出了不同局部扰动概率P时t=300,s内平均液相传质系数kavg随浓度扰动大小Dρ的变化关系．

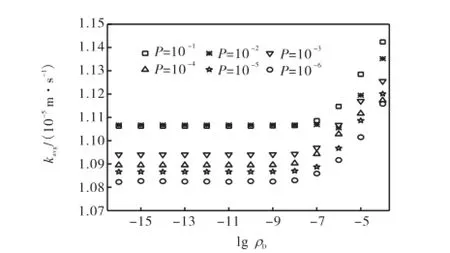
图3 不同P时kavg随ρD的变化关系Fig.3 Variations of kavgwith ρDfor different P

从图3中可以看出，给定P，kavg随着ρD的减小呈现出先减小后趋于稳定的变化趋势：当ρD＞10-9kg/m3时，kavg随着ρD的减小而减小；当0＜ρD≤10-9kg/m3时，kavg与ρD的取值基本无关．在0＜ρD≤10-9kg/m3的条件下，当10-6≤P≤10-1时，kavg存在一个稳定值，为(1.09±0.02)×10-5m/s，则相应的平均液相传质通量为(5.12±0.094)×10-5kg/(m2·s)，与文献[21]实验测量结果(300,s内平均液相传质通量约为6×10-5kg/(m2·s))吻合较好，从而说明了模型参数P和ρD取值范围的合理性．

2.2 Rayleigh对流结构

取计算区域高H=10,mm、宽L=20,mm，网格划分为200×400．图4给出了50,s、55,s、60,s和65,s时不同模型参数下溶质的浓度分布．当P=0.1、ρD= 10-12,kg/m3时，从图4(a)～(d)可以观察到Rayleigh对流的时空演化过程：在有界面扰动条件下，溶质首先在近界面发生扩散，约50,s左右，界面由于Rayleigh不稳定开始发生变形(见图4(a))；55,s时界面对流已经在多个Rayleigh不稳定区域开始发生(见图4(b))；随后对流发展成羽状对流结构，界面处高浓度液体以羽状对流结构逐步向下发展至液相主体(见图4(c)和(d))．这种Rayleigh对流的时空演化特征同实验观察结果基本一致[2-4]．

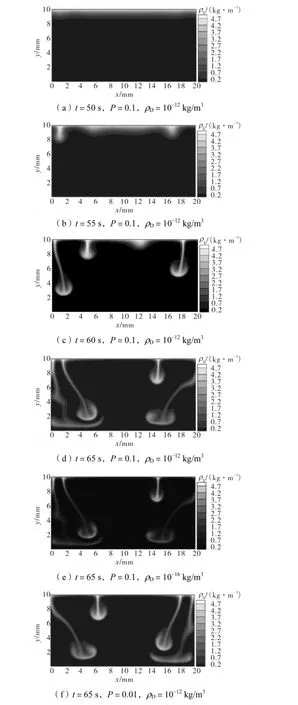
图4 50,s、55,s、60,s和65,s时不同模型参数下溶质的浓度分布Fig.4 Transient contours of solute concentration for different model parameters after 50,s，55,s，60,s，65,s

对比图4(d)和图4(e)可知，当局部扰动概率P一定时，羽状对流结构的数量、大小及产生位置与浓度扰动大小ρD基本无关．对比图4(e)和图4(f)可知，当ρD一定时，P对羽状对流结构的产生位置有一定的影响，但对其数量及大小基本无影响．

2.3 传质增强因子

发生Rayleigh对流时，液相传质系数比只依靠扩散传质时大，因此引出传质增强因子这一概念，将其定义为存在Rayleigh对流时的液相传质系数与只有扩散传质存在时(由渗透理论计算)的液相传质系数之比[8]．

根据模拟获得的浓度场，t时刻瞬时液相传质系数kins,t(m/s)计算式为

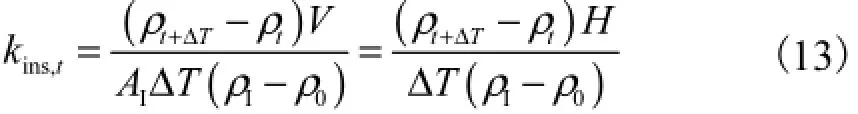
式中ΔT为时间间隔，取值为0.1,s．

由渗透理论预测的瞬时液相传质系数k0(m/s)ins,t可表示为

则瞬时传质增强因子可表示为

取计算区域高H=10,mm、宽L=20,mm，网格划分为200×400．图5给出了P=0.1、ρD=10-12,kg/m3条件下瞬时传质增强因子Fins随时间的变化关系．由图5可知，瞬时传质增强因子介于1～7之间，因此Rayleigh对流可以大大提高气液传质速率．

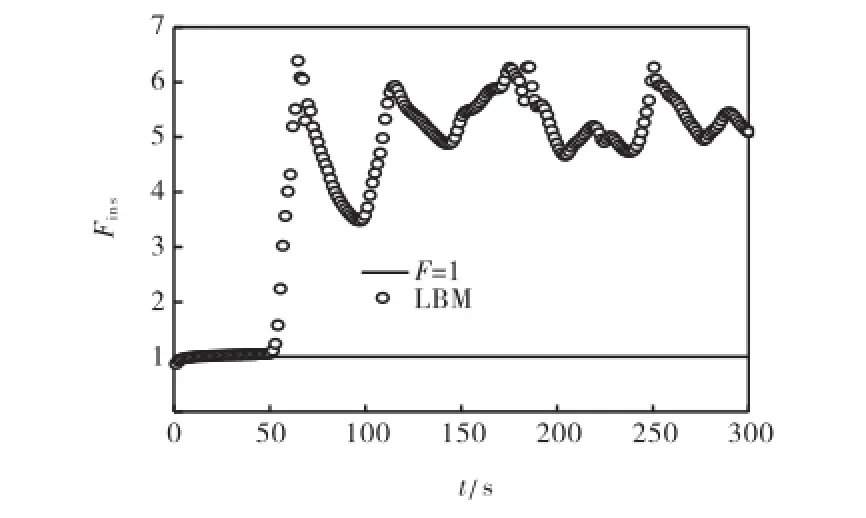
图5 P=0.1、ρD=10-12,kg/m3条件下Fins随时间t变化关系Fig.5 Variation of Finswith time t at P=0.1,and ρD=10-12,kg/m3

3 结 语

通过引入随机扰动模型，建立了模拟Rayleigh对流的带有双分布模型的二维格子Boltzmann方法．运用该方法对静止乙醇吸收CO2传质过程中液相Rayleigh对流现象进行模拟，结果发现，300,s内平均液相传质系数kavg随着ρD的减小呈现出先减小后趋于稳定的变化趋势；当0＜ρD≤10-9,kg/m3、10-6≤P≤10-1时，kavg存在一个稳定值(1.09± 0.02)×10-5,m/s．通过考察浓度分布结构，分析了Rayleigh对流的时空演化过程．另外，传质增强因子的模拟结果证明了Rayleigh对流能够有效地提高传质速率．因此，建立的LBM方法可有效模拟界面传质引发的Rayleigh对流现象，有助于加强对真实气液传质过程中Rayleigh对流的理解，为进一步探讨强化界面传质的机理和途径提供帮助．

［1］ Grahn A. Two-dimensional numerical simulations of Marangoni-Bénard instabilities during liquid-liquid mass transfer in a vertical gap[J]. Chemical Engineering Science，2006，61(11)：3586-3592.

［2］ 沙 勇，李樟云，林芬芬，等. 气液传质界面湍动现象投影观察[J]. 化工学报，2010，61(4)：844-847. Sha Yong，Li Zhangyun，Lin Fenfen，et al. Shadowgraph observation on interfacial turbulence phenomena in gas-liquid mass transfer[J]. CIESC Journal，2010，61(4)：844-847(in Chinese).

［3］ Barbosa J R，Ortolan M A. Experimental and theoretical analysis of refrigerant absorption in lubricant oil[J]. HVAC and R Research，2008，14(1)：141-158.

［4］ Okhotsimskiis A，Hozawa M. Schlieren visualization of natural convection in binary gas-liquid systems[J]. Chemical Engineering Science，1998，53(14)：2547-2573.

［5］ Sun Z F. Onset of Rayleigh-Bénard-Marangoni convection with time-dependent nonlinear concentration profiles[J]. Chemical Engineering Science，2012，68 (1)：579-594.

［6］ Tan K K，Tey B T，Tan Y W. Onset of natural convection in gas-gas system induced by bottom-up transient mass diffusion[J]. Engineering Applications of Computational Fluid Mechanics，2010，4(4)：475-482.

［7］ 陈 炜. 气液界面Rayleigh-Bénard-Marangoni对流现象实验测量及传质研究[D]. 天津：天津大学化工学院，2010. Chen Wei. Experimental Measurement of Gas-Liquid Interfacial Rayleigh-Bénard-Marangoni Convection and Mass Transfer[D]. Tianjin：School of Chemical Engineering，Tianjin University，2010 (in Chinese).

［8］ Sun Z F，Yu K T，Wang S Y，et al. Absorption anddesorption of carbon dioxide into and from organic solvents：Effect of Rayleigh and Marangoni instability[J]. Ind Eng Chem Res，2002，41(7)：1905-1913.

［9］ 付 博，袁希钢，陈淑勇，等. Rayleigh对流及其对界面传质影响模拟的格子Boltzmann方法[J]. 化工学报，2011，62(11)：2993-3000. Fu Bo，Yuan Xigang，Chen Shuyong，et al. Rayleigh convection and its effect on interfacial mass transfer by lattice Boltzmann simulation[J]. CIESC Journal，2011，62(11)：2993-3000(in Chinese).

［10］ Fu Bo，Yuan Xigang，Liu Botan，et al. Characterization of Rayleigh convection in interfacial mass transfer by lattice Boltzmann simulation and experimental verification[J]. Chinese Journal of Chemical Engineering，2011，19(5)：845-854.

［11］ Inamuro T，Yoshino M，Inoue H，et al. A lattice Boltzmann method for a binary miscible fluid mixture and its application to a heat-transfer problem[J]. Journal of Computational Physics，2002，179(1)：201-215.

［12］ Qian Y H，D'Humieres D，Lallemand P. Lattice BGK models for Navier-Stokes equation[J]. Europhysics Letters，1992，17(6)：479-484.

［13］ Bhatnagar P L，Gross E P，Krook M. A model for collision processes in gases. Ⅰ. small amplitude processes in charged and neutral one-component systems[J]. Physical Review，1954，94(3)：511-525.

［14］ Shan X W. Simulation of Rayleigh-Bénard convection using a lattice Boltzmann method[J]. Physical Review E，1997，55(3)：2780-2788.

［15］ Buick J M，Greated C A. Gravity in a lattice Boltzmann model[J]. Physical Review E，2000，61(5)：5307-5320.

［16］ Sukop M C，Thorne D T Jr. Lattice Boltzmann Modeling：An Introduction for Geoscientists and Engineers[M]. Netherlands：Springer，2006.

［17］ Shi Y，Zhao T S，Guo Z L. Finite difference-based lattice Boltzmann simulation of natural convection heat transfer in a horizontal concentric annulus[J]. Computers and Fluids，2006，35：1-15.

［18］ Tan K K，Thorpe R B. The onset of convection induced by buoyancy during gas diffusion in deep fluids[J]. Chemical Engieering Science，1999，54：4179-4187.

［19］ Arce A，Arce A Jr，Rodil E，et al. Density，refractive index，and speed of sound for 2-ethoxy-2-methylbutane+ ethanol+water at 298. 15,K[J]. Journal of Chemical and Engineering Data，2000，45(4)：536-539.

［20］ Takahashi M，Kobayashi Y. Diffusion coefficients and solubilities of carbon dioxide in binary mixed solvents[J]. Journal of Chemical and Engineering Data，1982，27(3)：328-331.

［21］ 林芬芬. 界面湍动现象的实验研究[D]. 厦门：厦门大学化学化工学院，2009. Lin Fenfen. Experimental Study on the Interfacial Turbulence Phenomena[D]. Xiamen：College of Chemistry and Chemical Engineering，Xiamen University，2009(in Chinese).

Simulation of Rayleigh Convection in Gas-Liquid Interfacial Mass Transfer Process by Lattice Boltzmann Method

FU Bo，YUAN Xi-gang，CHEN Shu-yong，LIU Bo-tan，YU Kuo-tsung
(State Key Laboratory of Chemical Engineering，School of Chemical Engineering and Technology，Tianjin University，Tianjin 300072，China)

Concentration gradient driven Rayleigh convection is an interfacial phenomenon usually observed in mass transfer processes. A random perturbation model characterizing interfacial disturbance was proposed and a twodimensional lattice Boltzmann method(LBM)with a double distribution model was implemented for simulating the interfacial mass transfer induced Rayleigh convection in gas-liquid mass transfer process of CO2absorption into liquid ethanol. In the simulation of the two-dimensional liquid-phase Rayleigh convection，CO2concentration at the interface was assumed to be constant. Through simulation，two parameters for the random perturbation model—the local perturbation possibility P and the perturbation magnitude ρD—were identified. The simulated results show that an average liquid-phase mass transfer coefficient has a stable value of(1.09±0.02)×10-5,m/s with the parameter values of 0＜ρD≤10-9kg/m3and 10-6≤P≤10-1. Through investigating concentration contour patterns，the temporal-spatial evolution of the convection was analyzed. A mass transfer enhancement factor was defined and evaluated based on the simulated results，and the interfacial mass transfer was shown to be effectively enhanced by the Rayleigh convection.

Rayleigh convection；lattice Boltzmann method(LBM)；interfacial mass transfer；liquid-phase mass transfer coefficient；mass transfer enhancement factor

TQ021.4

A

0493-2137(2012)07-0585-06

2012-01-14；

2012-04-19.

国家自然科学基金资助项目(20736005).

付 博（1984— ），男，博士研究生，fubo@tju.edu.cn.

袁希钢，yuanxg@tju.edu.cn.