基于模糊算法的风电储能系统的优化控制

张 坤 吴建东 毛承雄 陆继明 王 丹 黄 辉

（华中科技大学电气与电子工程学院 武汉 430074）

1 引言

风电系统由于风速、风向等自然条件的变化而不能持续地、稳定地输出电能，这会对电网的电能质量及其稳定性产生较大的影响[1-4]。因而，在系统中配置一定容量的储能装置将起到平抑功率波动、维持发电/负荷动态平衡、保持电压/频率稳定的作用，从而实现风力发电系统安全、经济、高效、优质地运行[5-8]。

就储能系统的技术性能而言，其容量配置得越大，对风电机组功率波动的平滑效果就会越好，但这也同时增加了系统的投资成本，不能很好地满足经济性要求。因此，对于一定容量的储能系统，如何通过对其自身的优化控制，来提高储能系统在风电系统中的技术性能，已成为目前迫切需要解决的问题。文献[7,8]在关于平滑风电功率波动的储能系统的优化控制方面已经取得了一定的研究成果。其中，文献[7]通过实时检测储能装置的荷电状态，相应地对并网功率参考值放大或缩小一定的倍数，以此来达到对储能装置荷电状态的控制。文献[8]通过加入一个反馈补偿量的方式来修正储能装置充放电功率的大小，从而能够有效地控制储能装置的荷电状态，避免出现过度充电或深度放电的状况发生。

本文以基于超级电容器的永磁直驱式风力发电系统为研究对象，通过实时检测超级电容器组的荷电状态SOC及其充放电状态，并将超级电容器组实时检测到的荷电状态与其参考值SOCref的偏差ΔSOC以及超级电容器组此时的充放电状态作为模糊控制器的输入，根据其偏差程度和充放电状态利用模糊规则来实时动态调节滤波时间常数T的大小，从而能够实时控制风电并网功率指令值，以达到实时动态调节超级电容器组充放电功率大小的目的，使超级电容器组能够避免出现过度充电或深度放电的状况，并向着适中的荷电状态转变。

2 基于储能的直驱风电系统

2.1 系统的工作原理

图1是本文采用的基于超级电容器的永磁直驱式风力发电系统的拓扑结构。电机侧变换器由三相不可控整流桥、滤波电容和Boost变换器构成，用于控制风力发电机的有功输出；电网侧变换器通过调节网侧的d轴和q轴电流，控制其直流侧电压和流向电网的无功功率，实现有功和无功的解耦控制，通常运行在单位功率因数状态。电网侧变换器的直流侧并入储能系统，该系统由超级电容器组以及双向DC-DC变换器等构成，用于控制风电系统的有功输出。

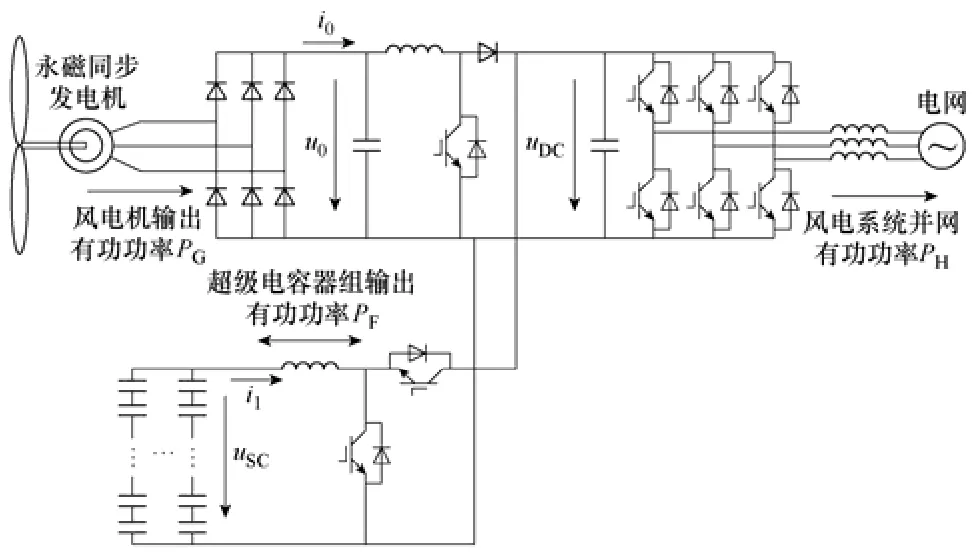
图1 基于超级电容器的永磁直驱风电系统Fig.1 Directly-driven wind power system using permanent synchronous generator based on ultra-capacitors

当风力发电机输出功率高于系统输出功率参考值时，即PG＞Pref，把多余的能量存储在储能设备中；当发电机输出功率低于系统输出功率参考值时，即PG＜Pref，可把储能设备中存储的能量释放出来为电网提供功率支撑。通过这种方式将能够有效地平滑风电机组输出功率的波动，使风电系统输出较为平滑的有功功率。

2.2 系统变换器的控制策略

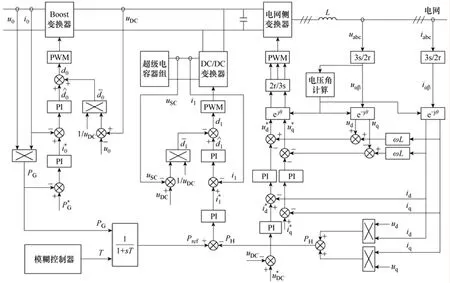
图2 基于超级电容器的直驱式风力发电系统中变换器的控制框图Fig.2 Block diagram of converters in directly-driven wind generation system based on ultra-capacitors

电机侧Boost变换器的控制框图如图2所示。图中，通过调节Boost变换器的功率参考值以实现风能的最大功率跟踪[9]，与风力发电机输出功率PG进行比较通过功率调节器得到Boost变换器的调制电流参考值，与升压斩波器输入电流i0进行比较再通过电流调节器得到升压斩波器占空比d0的反馈控制量，以达到电流对其参考值的快速跟踪，作为占空比d0的前馈控制量，可以抑制升压斩波器两端的电压波动给电流控制带来的干扰[10]。

连接超级电容器组的双向DC-DC变换器的控制原理如图2所示。图中，风力发电机发出的有功功率PG经一阶低通滤波器（时间常数T可变）得到并网功率参考值Pref，一阶低通滤波器的可变时间常数T由超级电容器组的荷电状态SOC与其参考值SOCref的偏差ΔSOC以及超级电容器组此时的充放电状态经模糊控制器得到，从而实时控制并网功率参考值Pref的输出，如图3所示。Pref与并网功率PH的偏差通过功率调节器得到双向DC-DC变换器的调制电流指令值；与其反馈值i1进行比较再通过电流调节器得到占空比d1的反馈控制量，以达到电流对指令的快速跟踪；作为占空比d1的前馈控制量，可以抑制电压波动给电流控制带来的干扰。

图3 模糊控制器的结构框图Fig.3 Block diagram of fuzzy logic controller

网侧变换器采用电压外环、电流内环的双闭环控制结构。通过电压环调节直流侧电压，直流电压调节器的输出作为d轴（有功）电流的参考值，使直流侧电压保持稳定；q轴（无功）电流参考值通常设为0，使系统运行在单位功率因数状态。

3 模糊控制器的设计

通常并网功率参考值Pref由风力发电机发出的有功功率PG经一阶低通滤波器得到，即

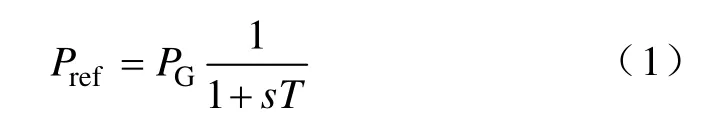
图4为风力发电机发出的有功功率PG=2MW时，并网功率参考值Pref随一阶低通滤波器时间常数T的变化波形图。由图4可知，时间常数T的取值越小，并网功率参考值Pref对风电机组输出功率PG的跟踪速度越快，反之则越慢。

图4 并网功率参考值Pref随时间常数T的变化特性Fig.4 Relations between the reference power transmitted to the grid and the time constant

图3 所示模糊控制器的作用就是根据超级电容器组的荷电状态以及其充放电状态给出合适的时间常数值T，从而实时动态调节风电并网功率参考值，以达到对超级电容器组输出功率及其荷电状态的实时控制。当超级电容器组荷电状态偏高时，若处在充电状态下，则减少时间常数，使并网功率参考值对风电场输出功率的跟踪速度变快，从而相对减少超级电容器组充电功率的大小，以减缓其荷电状态升高的速度，防止超级电容器组出现过度充电的状况；若处在放电状态下，则增大时间常数，使并网功率参考值对风电场输出功率的跟踪速度变慢，从而相对增大超级电容器组的放电功率，加速其荷电状态的降低，使之向着适中的荷电状态变化。反之亦然，当超级电容器组荷电状态偏低时，若处在充电状态下，则增大时间常数，使并网功率参考值对风电场输出功率的跟踪速度变慢，从而相对增大超级电容器组的充电功率，加速其荷电状态的回升，使之向着适中的荷电状态变化；若处在放电状态下，则减少时间常数，使并网功率参考值对风电场输出功率的跟踪速度变快，从而相对减少超级电容器组放电功率的大小，以减缓其荷电状态降低的速度，防止超级电容器组出现深度放电的状况。

根据超级电容器组控制系统的上述特性，本文采用两输入-单输出的二维结构形式。

输入1：荷电状态的偏差ΔSOC=SOC-SOCref，其中，SOC为超级电容器组的实时荷电状态，SOCref为超级电容器组荷电状态的参考值（本文取SOCref=60%），取其语言变量为E1，基本论域为[-40%，40%]，模糊论域为{-3,-2,-1,0,+1,+2,+3}，对应的模糊子集为{NB,NM,NS,ZO,PS,PM,PB}，分别表示当前超级电容器组的荷电状态，相对于设定值为{极低，很低，偏低，适中，偏高，很高，极高}。

超级电容器组荷电状态的参考值SOCref的选取取决于使超级电容器组能够正常工作所允许的荷电状态取值范围。若超级电容器组荷电状态在20%～100%时能够正常工作，则其参考值SOCref可取为60%，即：SOCref=20%+(100%-20%)/2=60%，以此作为超级电容器组适中的荷电状态。

输入2：超级电容器组的充放电状态，取其语言变量为E2。N表示超级电容器组处于放电状态，P表示超级电容器组处于充电状态。超级电容器组的充放电状态可由风电场输出功率PG与实际并网功率PT的大小来确定，若PG＜PH，表示超级电容器组处于放电状态，若PG＞PH，表示超级电容器组处于充电状态。

输出：一阶低通滤波器时间常数T，其基本论域为[0s,3000s],模糊论域为{0,1,2,3,4,5,6}，对应的模糊子集为{EL,VL,RL,ZO,RB,VB,EB}，分别表示滤波时间常数为{极小，很小，偏小，适中，偏大，很大，极大}。

滤波时间常数T的数量级选取主要取决于风电机组在一定时段（1min或10min）内的功率变化率，以及在该时段内风电并网功率所允许的最大变化率。若风电机组的功率变化率越大，风电并网功率所允许的最大变化率越小，则时间常数T的数量级会越高。反之，则会越低。

模糊控制器的输入输出隶属度函数都采用灵敏性较强的高斯隶属函数，去模糊化方法采用重心法。

根据前面描述的超级电容器组荷电状态的偏差大小及其充放电状态所对应的滤波时间常数输出的关系，给出模糊控制器的控制规则见下表。表中的模糊规则充分反映了时间常数T在不同的荷电状态偏差ΔSOC及其充放电状态下的变化特性。现从表中选取以下两条规则加以说明。

规则1：IF E1 is PB and E2 is P,THENTis EL。

规则2：IF E1 is NB and E2 is P,THENTis EB。

规则1解释为：当荷电状态SOC与其参考值SOCref偏差ΔSOC正极大时（PB）且超级电容器组处于充电状态（P）时，模糊控制器给出的时间常数输出为极小值（EL）。时间常数的最小值可取0，此时超级电容器组的充放电功率为0，其荷电状态不变化。

规则2解释为：当荷电状态SOC与其参考值SOCref偏差ΔSOC负极大时（NB）且超级电容器组处于充电状态（P）时，模糊控制器给出的时间常数T的输出为极大值（EB）。

表 模糊控制器规则表Tab.Rules of fuzzy controller

4 系统的仿真分析

利用Matlab/Simulink对图1所示的基于超级电容器的直驱式风力发电系统进行仿真。具体的仿真参数如下：风力发电机的额定功率为2MW，输出线电压有效值为690V，频率为50Hz；超级电容器组的额定电压为600V，容量为1MW/400(kW·h)；电网侧变换器的直流侧电压额定值为2 200V，功率器件为IGBT，开关频率均为5kHz；连接超级电容器组的双向DC-DC变换器的升压电感为0.1mH，电网侧变换器的直流侧电容为CDC=20mF，输出滤波电感为L=1.8mH。

风电机组输出有功功率PG如图5所示。风电系统并网功率PH在0时刻的初始值为0.87MW；超级电容器组在0时刻的初始荷电状态为80%；并假定超级电容器组荷电状态的正常工作范围为20%～100%；若超出这个范围，超级电容器组将停止工作。以下是采用模糊控制和未采用模糊控制时系统的仿真结果及其分析。

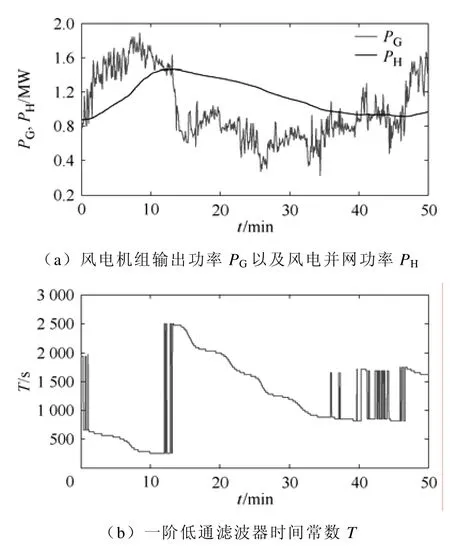
图5 采用模糊控制时系统的仿真波形Fig.5 Simulation results with fuzzy logic control strategy

当系统采用本文所提出的模糊控制时，其仿真结果如图5所示。当超级电容器组荷电状态较大时，若处于充电状态下，则减少滤波时间常数，降低其充电功率的大小，减缓其荷电状态的增加速度，防止出现过度充电的状况发生；若处于放电状态下，则增大滤波时间常数，提高其放电功率的大小，加速其荷电状态的降低，使之向着适中的荷电状态转变，与此同时对风电机组的功率波动还能起到较好的平滑效果。反之亦然，仿真结果很好地说明了所提控制方法的有效性和正确性。

当系统未采用本文所提出的模糊控制时，即采用固定的滤波时间常数T。一般情况下，滤波时间常数取得越大，则对风电机组功率波动的平滑效果会越好，但这同时也需要配置更大容量的超级电容器组，不利于经济性。图6所示为未采用模糊控制，滤波时间常数T=600s时的仿真波形。图6中看出，超级电容器组在12.517min时，其荷电状态将达到100%，之后一段时间将处于过度充电的状态。图7所示为未采用模糊控制，滤波时间常数T=400s时的仿真波形。由图7b可见，虽然在仿真时段内能够保证超级电容器组不出现过度充电或深度放电的状况，但对风电机组功率波动的平滑效果不如采用模糊控制时的平滑效果好。

图6 未采用模糊控制且T=600s时系统的仿真波形Fig.6 Simulation results without fuzzy logic control strategy and time constant T=600s

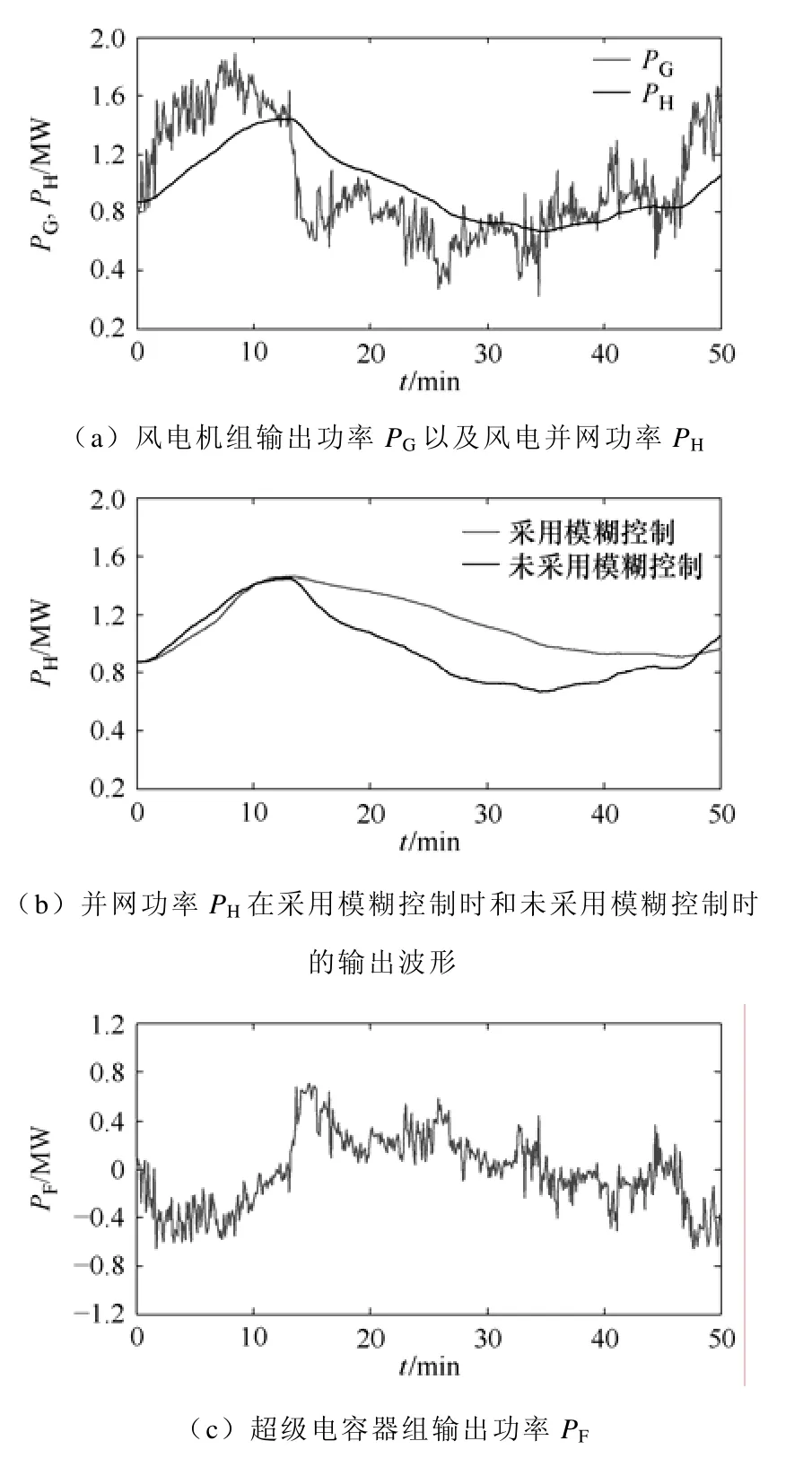
图7 未采用模糊控制且T=400s时系统的仿真波形Fig.7 Simulation results without fuzzy logic control strategy and time constant T=400s

5 结论

风电储能系统的优化控制在提高其技术性能和经济性方面将起到至关重要的作用。本文将模糊控制引入储能系统的优化控制中，根据储能系统实时的荷电状态及其充放电状态，通过模糊控制器实时地调节一阶低通滤波器的时间常数，从而在实现平抑风电机组功率波动的同时，还能够使储能系统避免出现过度充电或深度放电的状况，并向着适中的荷电状态转变。仿真结果验证了上述所提控制策略的正确性和有效性。

[1] 孙涛,王伟胜,戴慧珠,等.风力发电引起的电压波动和闪变[J].电网技术,2003,27(12): 62-66.Sun Tao,Wang Weisheng,Dai Huizhu,et al.Voltage fluctuation and flicker caused by wind power generation[J].Power System Technology,2003,27(12): 62-66.

[2] 迟永宁,王伟胜,刘燕华,等.大型风电场对电力系统暂态稳定性的影响[J].电力系统自动化,2006,30(15): 10-14.Chi Yongning,Wang Weisheng,Liu Yanhua,et al.Impact of large scale wind farm integration on power system transient stability[J].Automation of Electric Power System,2006,30(15): 10-14.

[3] 赵勇,胡雅娟,黄巍.风电场功率波动对电网电压影响[J] .吉林电力,2007,35(2): 22-24.Zhao Yong,Hu Yajuan,Huang Wei.Effect of wind farm fluctuation power on grid voltage[J].Jilin Electric Power,2007,35(2): 22-24.

[4] Moreno V C,Duarte A H,Garcia U J.Propagation of flicker in electric power networks due to wind energy conversions systems[J].IEEE Transactions on Energy Conversion,2002,17(2): 267-272.

[5] 张步涵,曾杰,毛承雄,等.电池储能系统在改善并网风电场电能质量和稳定性中的应用[J].电网技术,2006,30(15): 54-58.Zhang Buhan,Zeng Jie,Mao Chengxiong,et al.Improvement of power quality and stability of wind farms connected to power grid by battery energy storage system[J].Power System Technology,2006,30(15): 54-58.

[6] Luo C,Banakar H,Shen B,et al.Strategies to smooth wind power fluctuations of wind turbine generator[J].IEEE Transactions on Energy Conversion,2007,22(2): 341-349.

[7] Ushiwata K,Shishido S,Takahashi R,et al.Smoothing control of wind generator output fluctuation by using electric double layer capacitor[C].International Conference on Electrical Machines and Systems,Seoul,Korea,2007.

[8] Yoshimoto K,Nanahara T,Koshimizu G,et al.New control method for regulating state-of-charge of a battery in hybrid wind power/battery storage system[C].Power Systems Conference and Exposition,PSCE′2006: 1244-1251.

[9] 刘其辉,贺益康,赵仁德.变速恒频风力发电系统最大风能追踪控制[J].电力系统自动化,2003,27(20): 62-67.Liu Qihui,He Yikang,Zhao Rende.The maximal wind-energy tracing control of avariable-speed constant-frequency wind-power generation system[J].Automation of Electric Power System,2003,27(20):62-67.

[10] 陈瑶.直驱型风力发电系统全功率并网变流技术的研究[D].北京: 北京交通大学,2008.

[11] L Changling,H Banakar,S Baike,et al.Strategies to smooth wind power fluctuations of wind turbine generator[J].IEEE Transactions on Energy Conversion,2007,22(2): 341-349.

[12] R Cardenas,R Pena,G Asher,et al.Power smoothing in wind generation systems using a sensorless vector controlled induction machine driving a flywheel[J].IEEE Transactions on Energy Conversion,2004,19(1): 206-216.

[13] 何致远,瞿晓.基于电源滤波的三相PWM整流器模糊控制策略研究[J].电工技术学报,2006,21(4):107-110.He Zhiyuan,Qu Xiao.Study on fuzzy control strategy of three-phase PWM rectifier as an active current harmonic filter[J].Transactions of China Electrotechnical Society,2006,21(4): 107-110.

[14] 陈鑫兵,何礼高.基于模糊控制的三电平逆变器中点电位平衡策略[J].电工技术学报,2007,22(10):103-108.Chen Xinbing,He Ligao.Research on neutral point potential balance of three-level inverter based on fuzzy logic control strategy[J].Transactions of China Electrotehcnical Society,2007,22(10): 103-108.

[15] 曾光,苏彦民,柯敏倩,等.用于无功静补系统的模糊-PID控制方法[J].电工技术学报,2006,21(6):40-44.Zeng Guang,Su Yanmin,Ke Minqian,et al.A hybrid fuzzy and PID control method for static var compensation[J].Transactions of China Electrotehcnical Society,2006,21(6): 40-44.

[16] 唐杰,罗安,欧剑波,等.配电静止同步补偿器的模糊自适应PI控制策略[J].电工技术学报,2008,23(2): 120-126.Tang Jie,Luo An,Ou Jianbo,et al.Voltage control strategy of D-STATCOM based on fuzzy-PI controller[J].Transactions of China Electrotehcnical Society,2008,23(2): 120-126.