基于电网络理论的变电站接地网腐蚀及断点诊断方法

许 磊 李 琳

（华北电力大学新能源电力系统国家重点实验室 北京 102206）

1 引言

变电站接地网是维护电力系统安全可靠运行、保障运行人员和电气设备安全的重要措施，接地网导体的腐蚀、断裂或者漏焊等是造成系统故障的潜在因素，将会引发事故并带来巨大的经济损失[1,2]。地网接地性能一般由接地电阻的大小间接判断，但无法据此判断地网腐蚀情况，地网导体腐蚀甚至断裂时，接地电阻仍可能正常[3,4]。

从模拟电路故障诊断的理论可以知道，无论是何种方法建立的故障诊断方程，都是欠定的方程。对于变电站接地网，由于其设备的接地引线是有限的，因此构建的故障诊断方程也是欠定方程，欠定方程的有效求解问题一直是故障诊断领域讨论的问题[5]。

国内外学者在接地网诊断的研究中已经取得了很多成果，现有的方法主要有两大类：一类是基于电磁场理论的方法[6]，另一类是基于电路理论建立故障诊断方程的方法[7]。文献[8]对接地网的可测性进行了讨论。文献[9]提出了分层约简的方法。文献[10]采用灵敏度分析法建立诊断方程，并用能量损耗最低原理对方程求解。

本文把接地网等效成电阻网络，用PSpice软件计算得出其没有发生故障时所有可及节点对地的端口电阻的原始数据。假定地网若干支路发生腐蚀或断裂故障，用一个直流电流源依次在所有可及节点注入直流电流，测量所有可及节点对地的电压，计算得到端口电阻。针对故障前后接地网对应的两个相同拓扑结构的电阻网络，利用特勒根定理建立欠定的故障诊断方程。用优化的方法求解欠定方程组，得到各个支路故障前后电阻变化量，通过与原始支路电阻数据相比较，实现故障诊断。

为了验证分析方法，用电阻元件构造一个小型电阻网络并用钢筋焊接一个模拟接地网，在两个模型上开展模拟实验测量并用本文方法进行仿真计算。基于对计算结果和测量结果的比较，实现了对模拟地网故障的诊断，验证了本文接地网故障诊断方法的正确性和可行性。

2 基本原理

2.1 接地网模型

由于土壤电导率远远小于变电站接地网导体的电导率，直接测量变电站接地网下引线的电位时，接地网周围土壤对测量结果的影响可以忽略。如图1所示，变电站接地网可视为纯电阻网络，接地引线就是该网络的可及节点（△表示），整个接地网可以看成一个多端口网络。

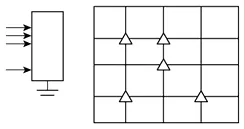
图1 变电站接地网模型Fig.1 Substation grounding grid model

将等效的电阻网络中的所有节点、支路按顺序编号，设支路数为b，节点数为n，可及节点数为m+1（其中一根为参考节点引线）。为消除电容耦合及电感耦合的干扰，测量中针对图1接地网中任意可及节点施加直流电流源激励[11,12]，新增加的支路编号为b+1。定义该网络的关联矩阵为A，节点电导矩阵为Gn，支路电导矩阵为Gb，支路阻抗矩阵为Rb，节点电压矩阵Un，支路电压矩阵Ub，支路电流矩阵Ib，节点注入电流列向量In。根据电网络理论可得

从而可以得到端口i，j的电阻值

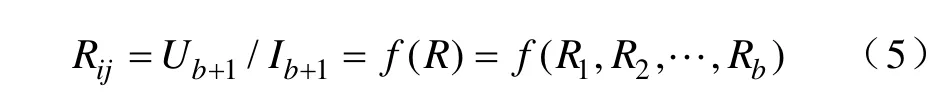
对于任意N端网络，如果能已知网络的结构和支路的电阻，以及激励的情况，那么可以根据节点分析法求出端口电阻。但是对于故障诊断来说，是由端口电阻值反推支路电阻值，式（5）给出了可及端点之间的端口电阻与接地网导体电阻的关系式。

2.2 故障诊断方程的建立

上节将腐蚀前的接地网视为一个具有b+1条支路，n个节点的网络N。其中，第b+1条支路连接在接地网的i，j端。在接地网上的第i，j端口加上一个恒定直流电流源，电流值I0。可以根据电路原理求出其端口电阻值Rij。当接地网发生腐蚀后的模型图视为网络N′，仍在其i，j端加电流源I0，求出。这两个网络的拓扑结构相同，唯一不同的是支路电阻值。

根据特勒根定理

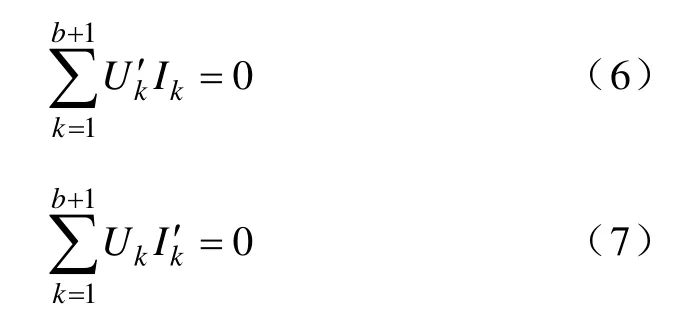
两个网络在i，j端的第b+1条支路的电流都为I0，即

代入式（6）和式（7）得

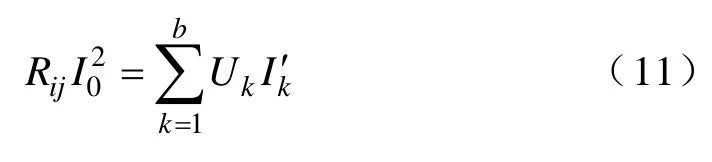
定义端口电阻增量ΔRij和支路电阻增量ΔRk

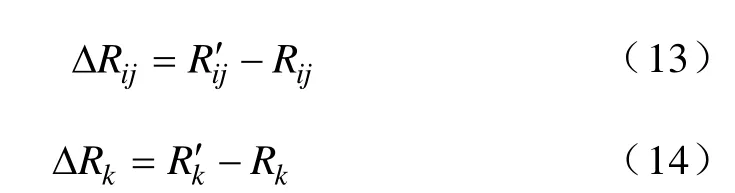
将式（12）减去式（11）得

这样就得到支路电阻变化和端口电阻变化的关系。对于有m个可及节点的网络，即有m个端口电阻值，可以建立一个m维的故障诊断方程组：

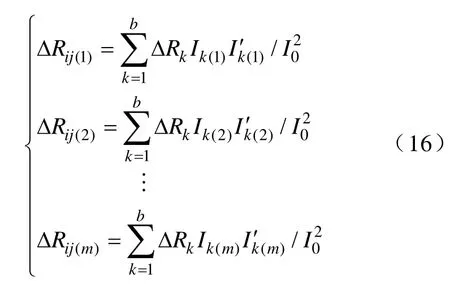
在上式的方程组中I0、ΔRij、Ik(k=1，2，…，b+1)是已知的。ΔRk、Rk′是待求变量，Ik′(k=1，2，…，b+1)是取决于Rk′的未知量。利用合适的优化算法解数学模型，就能得到故障后各段导体的电阻值，从而判断其是否发生腐蚀或断裂。

2.3 故障诊断方程的求解

从式（1 6）看出方程组是一个非线性的，而且是欠定的方程组（m＜b），无法直接求解，需要用合适的迭代算法去逼近非线性方程组的解。

（1）利用式（1）～式（4），由求得

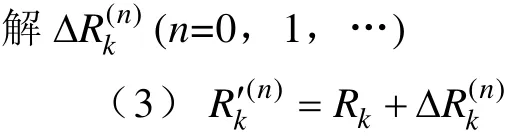
在此迭代过程中，是用线性方程组的解逼近原始的非线性方程组。由于越来越接近，因此用的值近似的误差也逐渐变小，线性方程组的解也更加逼近原始的非线性方程组的解。当（ε为设定的常数），停止迭代即得到最后结果，即。

在上述的迭代中，每一次迭代都要求解一个线性方程组，即步骤（2）中用式（16）求解。该欠定方程组解不唯一，但考虑到工程实际问题，在这些解中往往只有范围极小的一部分是合理的。这就需要用优化算法来求解该欠定方程组最合理的解。为此，构造一个有约束的线性规划问题来求解该方程组的最优解。

3 接地网故障诊断

3.1 诊断步骤

根据上一章介绍诊断方法，首先用PSpice软件仿真获取故障前的网络参数，然后建立故障诊断方程组，求解过程如下：

（1）在PSpice软件绘制接地网拓扑图，选择合适的节点作为公共点，设置各个支路电阻值。

（2）在公共节点与可及节点之间依次施加直流恒定电流源，由电路理论计算出各支路电流；再测量各个电流注入节点的电压值，从而求出该端口的电阻值Rij(m)。

（3）当一条或几条支路发生腐蚀及断裂故障时，其支路电阻增大。依次测试其电流注入端口的新电压值，求出该端口的新电阻值Ri′j(m)。

（5）代入诊断程序，用恰当的迭代方法使线性方程组的解逼近非线性方程组，对方程组进行优化求解，得到各个支路故障后的电阻值。

（6）分析结果，当可及节点数量较少而引起伪故障时，适当增加可及节点数量。

3.2 虚拟接地网故障诊断

3.2.1 单支路故障诊断

模拟接地网如图2所示。假设支路17被腐蚀，故障支路用“×”表示，正常支路电阻为0.05Ω，支路17电阻变为5Ω，增大99倍，任意选择可及节点，假设为2、8、9、14节点，在图中用“〇”表示，直流电源1A。考虑用尽量少的可及节点进行诊断，首先选择8、9两个可及节点进行计算，仿真结果用柱状图表示。

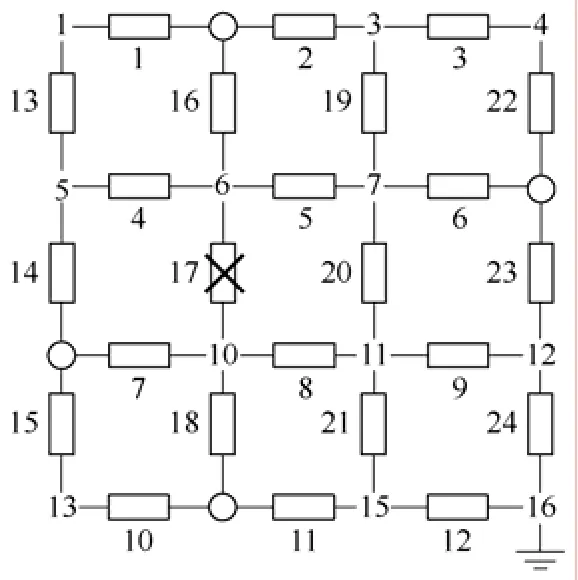
图2 支路17故障示意图Fig.2 Branch No.17 fault

第一次诊断结果如图3a所示，从图中可以看出，第16支路计算出的电阻增大倍数最大，为3.76倍。为检测故障的真伪，根据初步诊断结果，有目的的增加故障支路附近的可及节点进行诊断，伪故障的存在具有随机性，与算法相关。接着增加测量节点2的电压进行诊断，诊断结果为第17支路明显增大，如图3b。真实故障的位置和相关参数不随测量节点的增加而改变，说明第一次诊断的支路是伪故障。同理，验证支路17的故障真伪时，再增加可及节点14的电压进行诊断，诊断结果仍为第17支路故障，增大10.12倍，如图3c。此诊断结果的位置和数值与前一次相比变化不大，可以确认第17支路是真实故障，而其他支路变化不大，表明故障唯一。虽然没有诊断出设定的支路电阻值增大99倍，但是此结果依旧可以明显看出故障所在位置，诊断结果与设定的情况相符合。

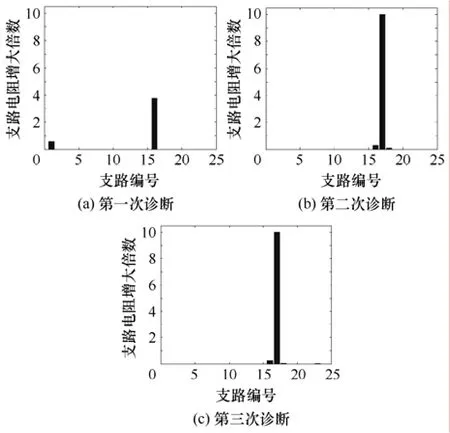
图3 单支路故障诊断结果Fig.3 Diagnosis results of single branch fault

3.2.2 双支路故障诊断

方法和步骤同上，假设支路6、8腐蚀，其支路电阻变为5Ω，其他支路为0.05 Ω，可及节点选择同上，依旧为2、8、9、14节点。考虑到用尽量少的节点诊断，仍然首先选用8、9节点，结果如图4a所示。8号支路被明显诊断出故障，同时1号支路也有明显增大。接着增加节点2的电压进行诊断，诊断结果如图4b所示，此时6支路也被诊断出来了，1号支路的增大倍数明显减小。再增加节点14的电压进行诊断，结果如图4c，6号支路增大12.41倍，8号支路增大11.13倍，故障被明显诊断出来，而且1号支路的伪故障也消失了。

图4 双支路故障诊断结果Fig.4 Diagnosis results of double branch fault

诊断出的结果与设定的情况一致，说明本文的腐蚀诊断方法能正确诊断出小型接地网的双支路腐蚀的情况。

4 模拟实验验证

实际构造一个小型电阻网络，如图5所示，每段支路由3.3Ω的电阻构成。拓扑图以及节点、支路编号与图2一致，规定电流正方向从左到右，从上到下。可及节点仍选择2、8、9、14节点，在这些节点中轮换注入1A的电流源激励。

图5 用电阻元件搭建的模拟接地网Fig.5 Model of grounding grid

其基本思路是在网络完好时施加激励并测量选定的可及节点电压值，计算其端口的电阻值；然后将接地网的某段支路设置为故障支路，接着对故障前已选择的那些节点再次测量其电压值，计算新的端口电阻值，根据截断前后端口电阻的差值，代入程序进行诊断并与实际情况比较看是否相符。

4.1 单支路故障诊断

把该支路（仍设置17号支路）分别用35Ω和155Ω的电阻替换（模拟腐蚀），最后截断该支路（模拟断裂）。在用35Ω替换时，诊断结果为17号支路增大倍数5.92倍；用155Ω替换时，增大倍数为7.17倍。结果虽然不能精确测出放大倍数，但是可以明显得出是该支路发生了故障。实验结果图6所示。

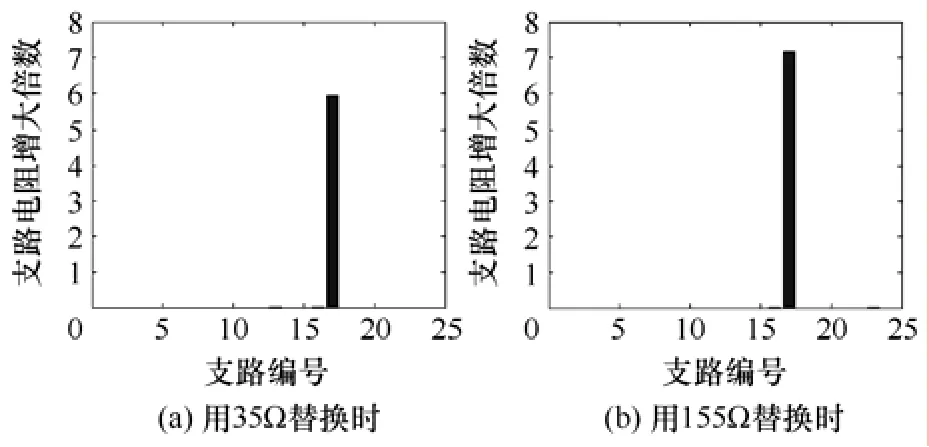
图6 故障诊断结果Fig.6 Fault diagnosis results

支路截断时的实验数据如表1所示（公共节点是16号节点），其中理论值是由PSpice软件仿真得来。网络可及节点间电阻的理论值和测量值变化都很小，这些变化中最大的是故障支路附近的端口电阻值，但增加得仍很小，说明由于接地网本身电阻值很小且并联层次很多，一条支路的变化对节点间的端口电阻值的影响很小，而对自身附近节点的端口电阻影响才比较明显。

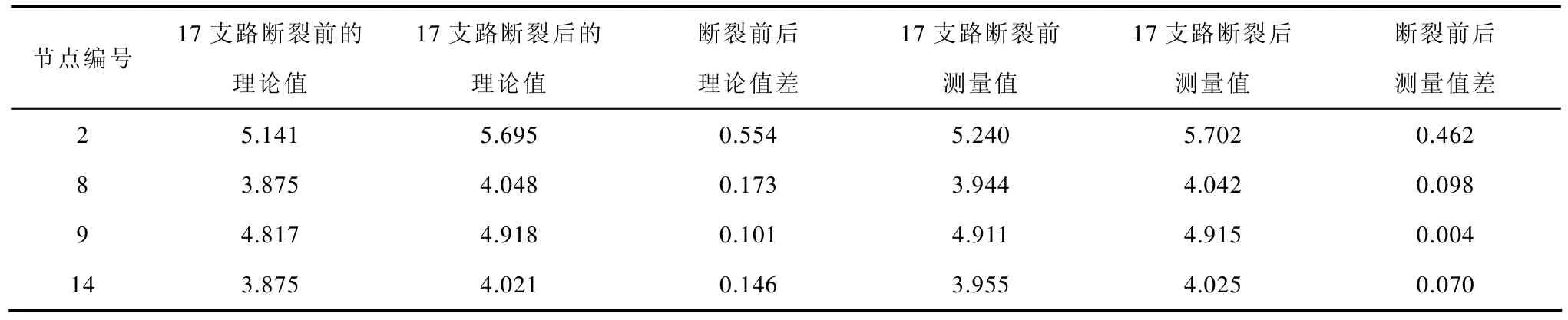
表1 单支路断裂前后端口电压数据Tab.1 Experimental data of single branch breaking （单位：V）

由于注入的电流源为1A，故端口电阻值即为测量电压值。将表1最后一列数据代入诊断程序进行计算，结果如图7a所示，与图7b所示的用理论值（表中第四列）进行诊断结果相比，在计算出的17支路增大倍数上不同，增大7.26倍，比理论值10.12倍略小。

4.2 双支路故障

仍然设置6号、8号支路断裂，实验测量的诊断结果如图8a所示，6号、8号支路分别增大7.7和6.98倍，诊断结果的放大倍数比图8b理论仿真结果稍小，但也是可以接受的。

为了更加真实地模拟变电站接地网，用直径6.5mm的钢筋焊接4×4模拟地网，该网络的支路电阻值近似为1mΩ，网格为25节点40条支路。拓扑图、钢筋地网和实验设备如图9所示。节点编号和支路编号标于图中，“〇”为随机选择的可及节点。由于支路电阻值很小，而实验时测量设备的精确度和测量误差对结果有较大影响，故仅对单支路断裂进行了模拟实验。如图9所示截断7号支路。

图7 单支路故障诊断结果Fig.7 Diagnosis results of single branch fault

图8 双支路故障诊断结果Fig.8 Diagnosis results of double branch fault

本次实验随机选择的可及节点是4、7、15、18、21节点，在可及节点中轮换注入1A的直流电流源，为了减小接触电阻等测量误差，在选择测量的可及节点处，用铜丝缠绕并垂直向上来模拟接地引线，以方便实验时测量。由于在实际的接地网诊断中，只能测量故障后的网络；故障前的地网参数是通过拓扑图计算得出的。该次试验的数据如表2所示。

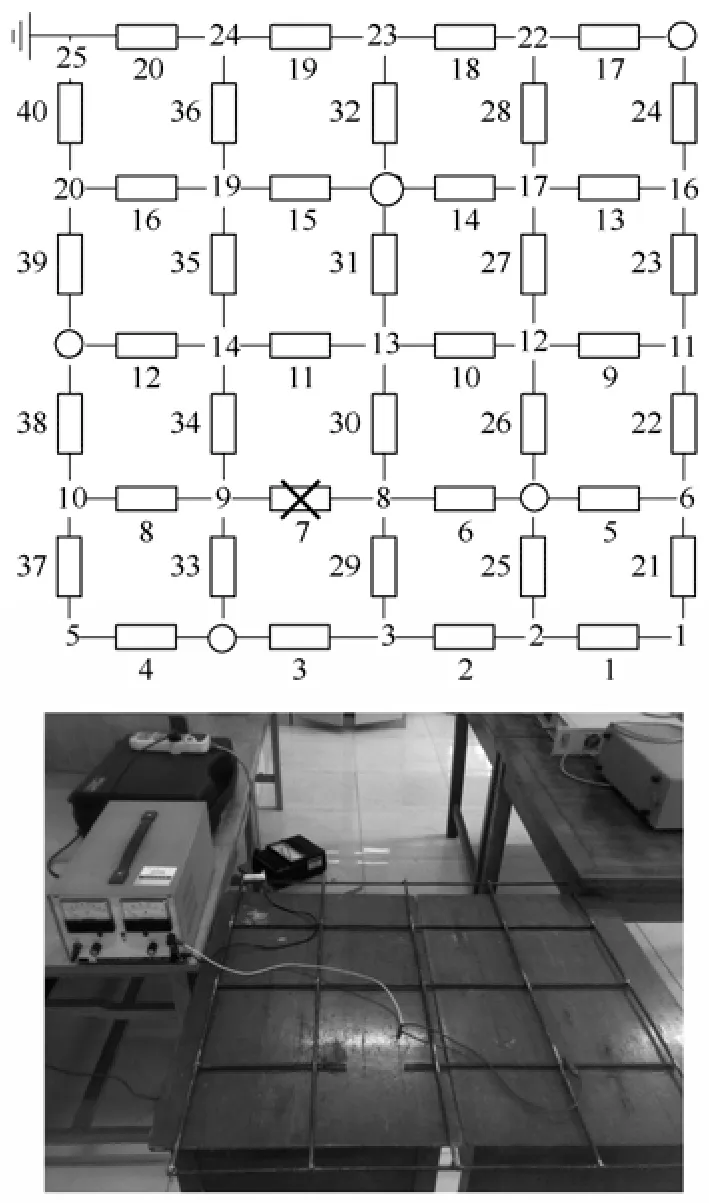
图9 拓扑图、钢筋地网和实验设备Fig.9 Topology,steel grid,experimental equipment

表2 模拟地网断裂前后端口电压数据Tab.2 Experimental data of grounding grid break （单位：mV）

由于注入的电流源为1A，故端口电阻值等于测量电压值。分别用支路7断裂前后的端口电阻变化的理论值与实际测量值进行对断裂支路的诊断，结果对比如图10所示。

用第四列的理论值代入程序诊断出7号支路放大倍数为10.81，最后一列的实际值诊断结果为6.16。实际的结果比理论的结果在增大倍数上有所减小，而且其他支路的伪故障增大倍数有所放大。虽然理论与实际结果都没有精确的诊断出正确的放大倍数，但是都可以准确地计算出是7号支路发生了故障，诊断结果与实际设定的情况相符合，从而验证了该理论的可行性。

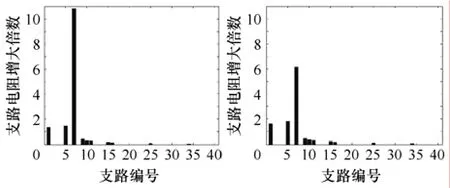
图10 理论与实际诊断结果对比Fig.10 Theory and practical diagnosis results contrast

5 结论

将实际的接地网近似等效成纯电阻网络，根据故障诊断理论和特勒根定理，建立了接地网的故障诊断方程。在建立的数学模型中，利用优化方法较好地解决了方程组的欠定问题，计算结果与实际情况较好的吻合。针对模拟接地网进行仿真，代入诊断程序计算，最后通过焊接真实接地网实验，验证了本文理论和方法的有效性。

[1] 张晓玲,黄清泉.电力系统接地网故障诊断[J].电力系统及其自动化学报,2002,1(3): 49-51.Zhang Xiaoling,Huang Qingquan.Fault diagnosis of grounding grid of electric power plants and substations[J].Electric Power System and Its Automation Journal,2002,1(3): 49-51.

[2] 赵志斌,崔翔,李琳.复杂土壤结构中接地网接地性能分析[J].华北电力大学学报,2006,3(4): 33-36.Zhao Zhibin,Cui Xiang,Li Lin.Analysis of grounding grids buried in complex soil[J].Journal of North China Electric Power University,2006,3(4):33-36.

[3] 刘渝根,滕永禧,陈先禄.接地网腐蚀的诊断方法研究[J].高电压技术,2004,30(4): 19-22.Liu Yugen,Teng Yongxi,Chen Xianlu.A method for corrosion diagnosis of grounding grid[J].High Voltage Engineering,2004,30(4): 19-22.

[4] 刘洋,崔翔,赵志斌,等.基于电磁感应原理的变电站接地网腐蚀诊断方法[J].中国电机工程学报,2009,29(4): 97-103.Liu Yang,Cui Xiang,Zhao Zhibin,et al.Method of corrosion diagnosis of substations’ grounding grids based on electromagnetic induction theory[J].Proceedings of the CSEE,2009,29(4): 97-103.

[5] 张晓玲,陈先禄.优化技术在发变电所接地网故障诊断中的应用[J].高电压技术,2000,26(4): 64-67.Zhang Xiaoling,Chen Xianlu.The technique of the optimization applied in the grounding grid’s failure diagnosis of the power plant and substation[J].High Voltage Engineering,2000,26(4):64-67.

[6] 刘洋,崔翔,赵志斌,等.变电站接地网腐蚀诊断磁场检测系统的设计与应用[J].电工技术学报,2009,24(l): 176-182.Liu Yang,Cui Xiang,Zhao Zhibin,et al.Design and application of testing mgnetic field system for corrosion diagnosis of grounding grids in substation[J].Transactions of China Electrotechnical Society,2009,24(l): 176-182.

[7] 何智强,文习山.一种地网腐蚀故障诊断的新算法[J].高电压技术,2007,33(4): 83-86.He Zhiqiang,Wen Xishan.Novel algorithm for fault diagnosis of grounding grid[J].High Voltage Engineering,2007,33(4): 83-86.

[8] 刘健,王树奇,李志忠.接地网腐蚀故障诊断的可测性研究[J].高电压技术,2008,34(1): 64-69.Liu Jian,Wang Shuqi,Li Zhizhong.Testability of grounding grids corrosion diagnosis[J].High Voltage Engineering,2008,34(1): 64-69.

[9] 刘健,王树奇.基于分层约简模型的接地网故障诊断软件设计[J].计算机工程与应用,2008,44(25): 51-55.Liu Jian,Wang Shuqi.Software design of grounding grid corrosion diagnosis based on hierarchical simplification of network topology[J].Computer Engineering and Applications,2008,44(25): 51-55.

[10] 肖新华,刘华.接地网腐蚀和断点的诊断理论分析[J].重庆大学学报,2001,24(3): 72-75.Xiao Xinhua,Liu Hua.Analysis of theory and method about the corrosion as well as the broken point of the grounding grid[J].Journal of Chongqing University,2001,24(3): 72-75.

[11] Xu Huizhong.The research of the grounding grid diagnosis[J].Journal of Nanjing Institute of Industry Technology,2007,7(4): 18-20.

[12] Qiu Qirong,Wang Shurong.Preconditioned land weber iteration algorithm for grounding grid fault diagnosis[C].Proceedings of the 8th International Conference on Machine Learning and Cybernetics,Baoding,2009.

[13] Zhang Bo,Cui Xiang,Li Lin.Diagnosis of breaks in substation’s grounding grid by using the Electromagnetic method[J].IEEE Transactions on Magnetic,2002,38(2): 473-476.

[14] 褚洪生,杜增吉.MATLAB优化设计实例指导教程[M].北京: 机械工业出版社,2006.

[15] 吴祈宗,郑志勇.运筹学与最优化MATLAB编程[M].北京: 机械工业出版社,2009.