基于三线DFT的航空电源频率实时检测算法

肖 鲲 王莉娜 M.Khurram Shahzad

（北京航空航天大学自动化科学与电气工程学院 北京 100191）

1 引言

现代航空技术的总趋势是发展多电和全电飞机。多电和全电飞机电源体制的主流趋势是采用大容量变速变频交流发电技术，产生360～800Hz变频交流电[1]。静态无功补偿器、有源电力滤波器、背靠背变换器及矩阵变换器等系统的网侧电路由可控功率器件组成，实时频率信息是实现功率器件开关控制、参考坐标变换、有功功率和无功功率计算的重要基准。因此，为保证机载电气设备正常工作，航空电源频率的高精度与实时检测至关重要。

目前，国内外已提出多种频率检测算法检测电力系统频率。过零检测法[2]的原理是通过检测过零点的时间差来计算频率，计算量小，方法简单，但动态性能较差，且对直流分量和噪声干扰敏感，检测的精度不佳。Prony检测法[3,4]是使用指数函数的线性组合来描述等间距采样数据的数学模型，缺点是算法所需的复数乘法和求解二元方程计算量大，硬件实现困难，且对信噪比的要求较高。卡尔曼滤波法[5]对离散随机动态过程及其噪声进行变换，在协方差最小的原则下递推估计状态矢量，但由于受到算法饱和现象的限制，当系统参数发生变化时，需重置协方差矩阵，算法较复杂。锁相环（Phase Locked Loop,PLL）检测法[6,7]通过坐标旋转提取dq轴分量，以相位为反馈量对q轴分量进行零值跟踪，动态性能较好，但是PI调节器需精心设计，且系统稳定性、稳态误差易受所选参数影响。离散傅里叶变换（DFT）在频率检测中得到了广泛应用，但只能用于整数次谐波，由于采样点数的限制，出现频谱泄露和栅栏效应[8]。另外，电力系统的频率检测法还有最小二乘法[9]、多信号分类（Multiple Signal Classification,MUSIC）算法[10]和自适应陷波（Adaptive Notch Filter,ANF）算法[11]等。

本文推导了加汉宁窗后基波频率与3条离散谱线幅值的数值关系，提出基于三线DFT的航空电源频率检测算法。该方法克服了DFT的栅栏效应，实现宽范围连续频率检测。结合电力系统特点分析了无主瓣幅值频谱泄露的参数选择方法，并在双级矩阵变换器实验样机上实现该算法。仿真和实验结果表明了算法的有效性。

2 三线DFT算法数学模型

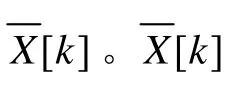
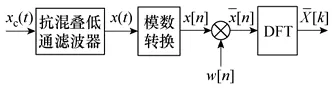
图1 时域信号傅里叶分析过程Fig.1 Process of Fourier analysis in time domain

设时域下连续信号为

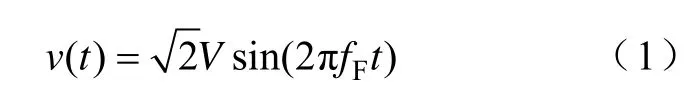
式中，V为时域信号有效值；fF为基波频率。

对连续时域信号离散化采样，采样时间间隔为Ts，采样点数为N，则离散序列为

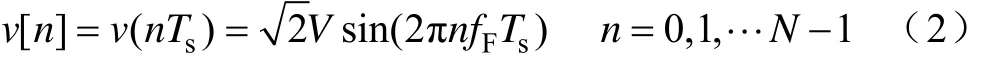
对离散序列加窗，考虑窗函数的主瓣宽度和相对旁瓣幅值，选用汉宁窗

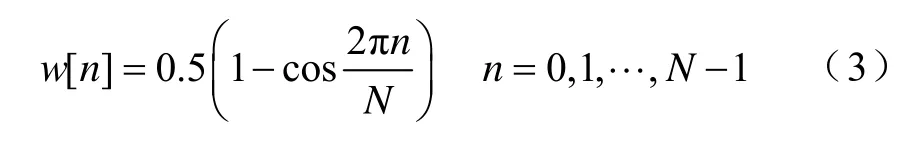
加窗后的离散信号为

对式（4）进行DFT，得

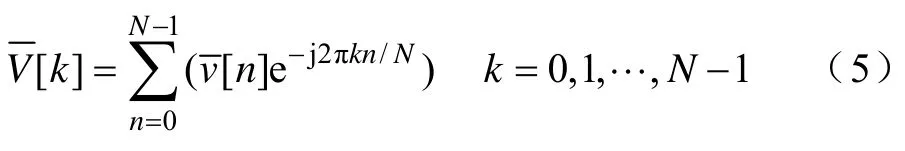
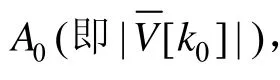
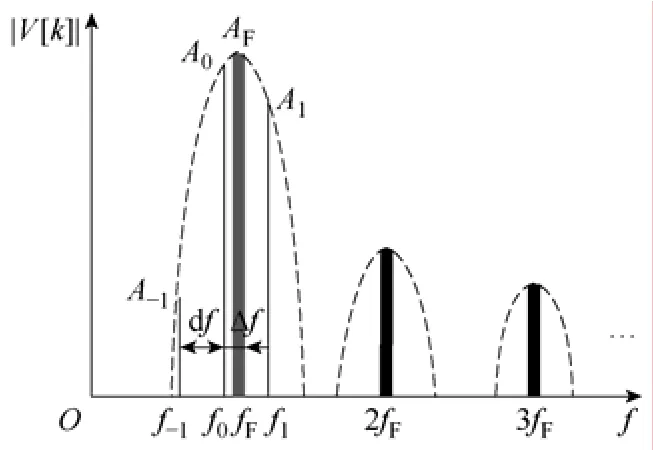
图2 加窗对幅度谱影响示意图Fig.2 Sketch of amplitude spectrum after windowing

从图2中可以看出，如果时域信号为fF、2fF、3fF等频率分量的合成，其无限长序列的频域分析结果应为fF、2fF、3fF等频率处的离散谱线，其余频率处谱线幅值为零。但由于对无限长序列的截断和加窗的影响，fF、2fF、3fF等频率分量的主瓣幅值沿虚线扩展（旁瓣幅值未画出），其中基波频率fF主瓣幅值沿虚线扩展到离散频率f0、f-1和f1上。如果能够根据f0、f-1和f1三条离散谱线幅值确定主瓣中心位置，那么基波频率fF即可得到。

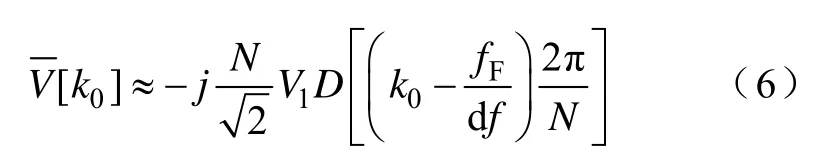
式中，D[·]为中间函数

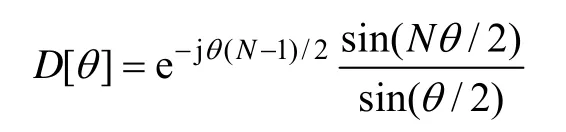
设a=A1/A0，b=A-1/A0，可以证明[12]

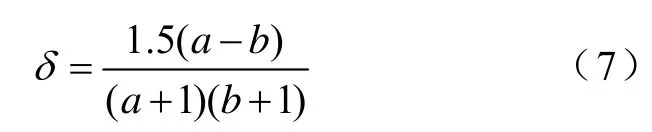
把式（7）代入fF=(k0+δ)df，得

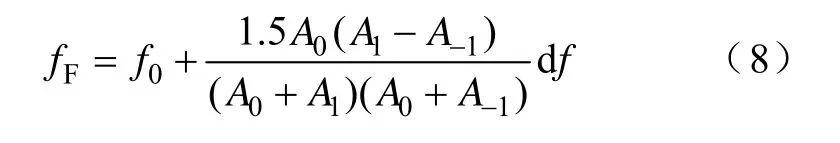
传统DFT只能得到N条离散谱线幅值，因存在栅栏效应，无法得到离散谱线间的频谱信息。如提高频率分辨率则需相应增加采样点数，使DFT计算量大幅增加。

由式（8）可知，已知fF主瓣区域的3条离散谱线幅值，则可计算连续频谱信息，得到基波频率。该算法在保证加窗后各频率分量主瓣互不重叠前提下，减少采样点数N不影响对连续基波频率的计算，计算量得以显著减小。

3 频率检测算法与参数选择

结合电力系统频谱特点，把三线DFT算法应用于航空电源频率实时检测。采用旋转坐标法计算3条离散谱线幅值，分析采样参数和频率初值取值方法，得到算法参数选择步骤。

3.1 旋转坐标法计算谱线幅值

设三相输入电压矢量为

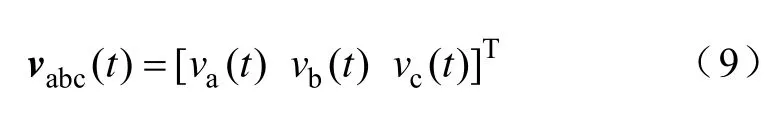
为方便DFT，对其进行克拉克变换，得两相坐标系下的电压矢量为

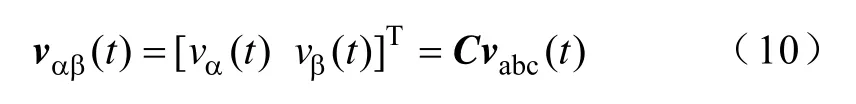
式中，C为克拉克变换矩阵

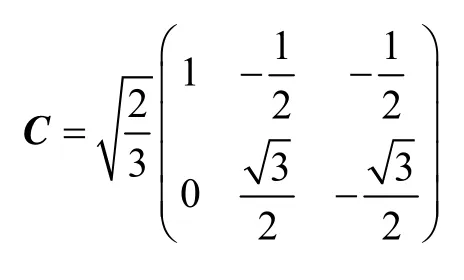
两相坐标系下的电压矢量vαβ(t) 亦可用复数表示

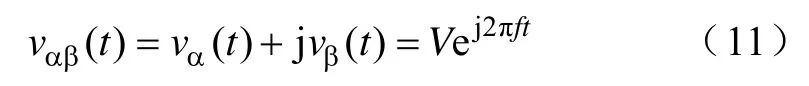
式中，V为矢量幅值；ej2πft为旋转算子；Vej2πft表示矢量以ω=2πf的角速度在复平面旋转。如对vαβ(t)进行旋转坐标转换，乘以旋转算子e-j2πft，在角速度为ω=2πf的旋转坐标系下观察，vαβ(t)为静止矢量，即直流量

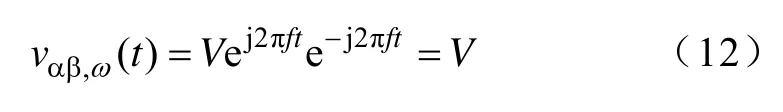
实际的电源波形可分解为基波和m(m=2,3,…)次谐波的合成，基波和m次谐波分别以频率f=fF和f=mfF在复平面上旋转，可用复序列表示为

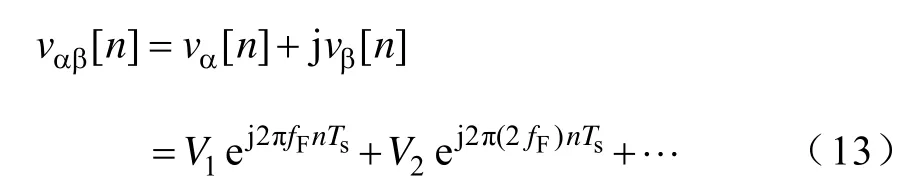
同上述，采用旋转坐标法，分别对加窗后序列vαβ[n]乘以旋转算子e-j2πf0nTs、e-j2π(f0-df)nTs和e-j2π(f0+df)nTs，即在频率分别为f、f和f的旋转

0-11坐标系上观察，A0、A-1和A1应为静止谱线幅值，为直流量。由式（5）可知，当k为零时，可得直流量

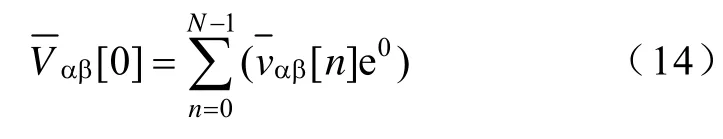
采用旋转坐标法求取离散谱线幅值，物理概念清晰，坐标旋转后只需执行加法运算。其优点体现在：一方面，直接进行DFT时每次采样需计算N次与旋转算子的复数乘法，而旋转坐标法每次采样只需计算1次复数乘法，后续计算可直接引用结果，计算量得到显著减小；另一方面，直接进行DFT，fF估计值只能取特定离散频率kdf处，而旋转坐标法可根据对fF的估计值任选旋转频率，不受特定频率限制。

3.2 参数选择

三线DFT的频率检测算法，需选择的参数有采样时间间隔Ts、采样点数N、频率分辨率df及频率估计初值f0。

Ts的取值参照乃奎斯特采样定律。采样时间间隔Ts=1/fs，其中fs为采样频率。根据乃奎斯特采样定律，fs为信号频率的两倍以上，则不会产生混叠现象。一般的航空电力变换器控制器中，fs与脉宽调制（PWM）频率（5～20kHz）一致，比基波频率高一个数量级，满足奎斯特采样定律，fs取PWM频率即可。

N的取值大小需谨慎权衡多方面因素：N的取值越大，窗函数的主瓣越窄，发生泄漏越弱，谱线幅值精度越高，但相应的算法运算量也越大，影响算法的实时性；相反，N的取值较小，窗函数的主瓣加宽，基波和谐波的谱线幅值可能相互发生泄漏，甚至无法分辨，但是算法的计算量会相应减小（汉宁窗的最大旁瓣幅值相对主瓣为－31dB，其幅值较小，文中忽略旁瓣的影响）。为使频域下各谱线的主瓣互不重叠，主瓣宽度应小于频域下相邻谱线频率差值，即flobe＜ΔfT；对于汉宁窗，主瓣宽度flobe=4/(NTs)。电源系统中无偶次谐波，相邻谱线频率差为2倍的基波频率，可得主瓣互不重叠的条件为

频率分辨率df=1/(NTs)，由式（8）可知，df越大，算法的频率检测范围越大。算法中假定f0是距fF最近的频率值，可知频率检测范围为

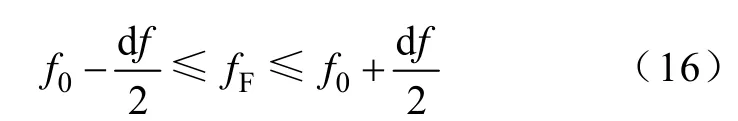
在满足乃奎斯特采样定律和不发生泄漏的前提下，N和Ts尽量取较小值，可得较大df值，使算法具有较大的频率检查范围。

f0是距fF最近的离散频率值，其对应的谱线A0应为三条谱线中最大。在航空电源系统中，f0的取值可根据过零点检测大致估计其初值，如按旋转坐标法计算A0、A-1和A1后，A0不为最大值，可增加（A1最大）或减少（A-1最大）f0，进行迭代计算，直至A0最大。由式（16）可知，改变f0的步长为df/2，迭代的频率检测范围既不重复，又无遗漏，因此具有最高效率。

综上所述，三线DFT的频率检测算法参数选择步骤如下：

（1）由控制器的采样频率fs确定Ts=1/fs，fs一般可满足乃奎斯特采样定律。

（2）由式（15）确定N的最小值。

（3）估计f0初值，采用步长为df/2的迭代法计算A0、A-1和A1三条谱线幅值，直至A0为最大值。

采用所选参数，对航空电源频率的实时检测的软件框图如图3所示。三相采样电压值经克拉克变换后变为αβ坐标系下的序列，分别对其进行f0、f-1和f1的坐标旋转，求和得到A0、A-1和A1的谱线幅值，最终利用式（8）得到基波频率fF。每次采样后对序列进行先入先出（FIFO）数据更新，只需进行一次旋转算子的复数乘法运算。频率检测中，一旦A0不为三条谱线中的最大值，执行迭代，直至A0为最大值，保证算法正确执行。

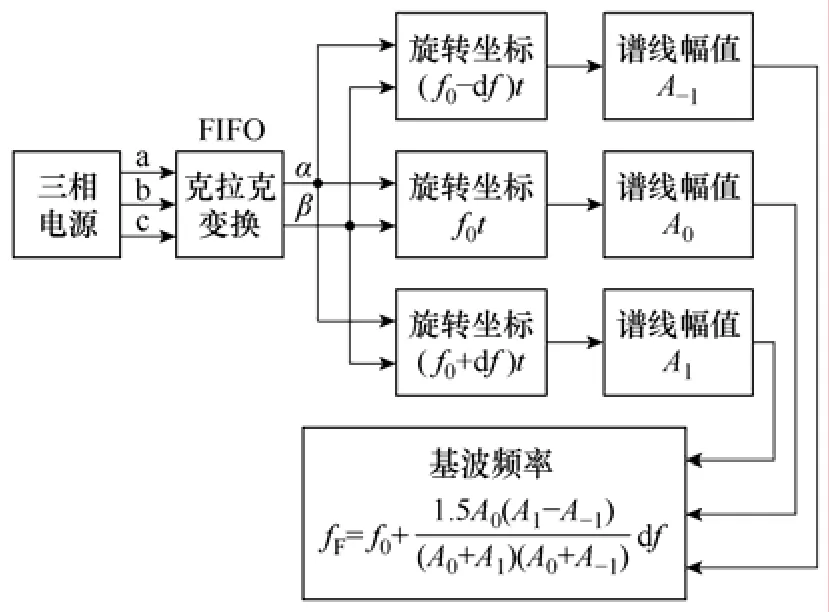
图3 三线DFT频率检测算法软件框图Fig.3 Diagram of frequency estimation based on 3-line DFT

4 仿真与实验验证

4.1 与PLL算法仿真对比

使用Matlab搭建仿真模型，把文中算法与PLL算法进行对比。PLL算法在理想电源系统下，采样结果虽尚好，但在含有谐波时，采样性能有所下降。而一般实际系统中均含有谐波，因此仿真该条件下的航空电源参数：设置电源基波幅值为115V，电源频率变化范围为360～800Hz，各次谐波相对基波幅值如下表所示。三线DFT算法中，采样频率fs为10kHz，由式（15）得N的最小值为55.5，取N=60，因此频率分辨率df为167Hz。由式（16）可知，该算法的频率检测范围为。分别对电源频率的阶跃变化和斜坡变化进行仿真。

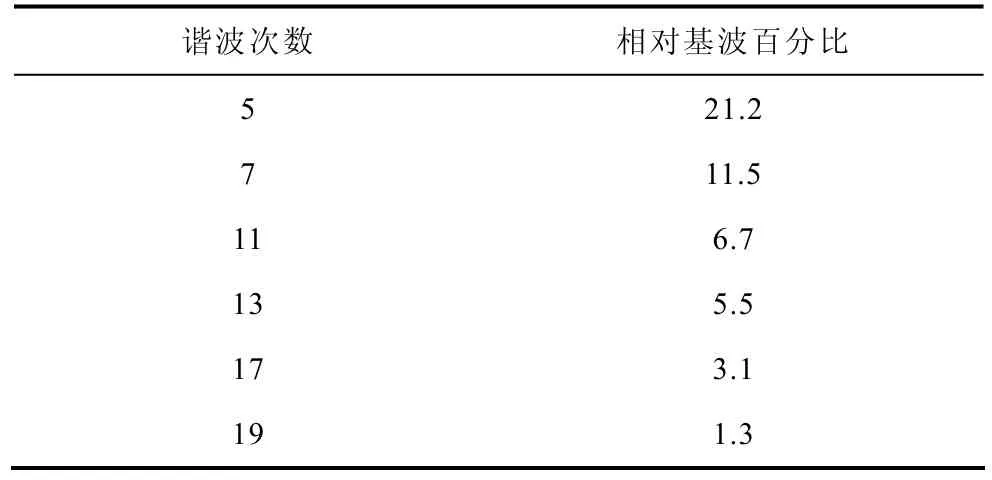
表 仿真模型中电源谐波参数Tab.Parameters of power source in simulation module

图4为三线DFT算法的阶跃响应，电源的初始频率为400Hz，在0.15s处突加10Hz的阶跃量。f0的初始值设为430Hz。由图4仿真结果可见，算法的检测值对实际频率的跟踪较好，无超调和振荡，延迟约为8ms，稳态误差小于0.1Hz。

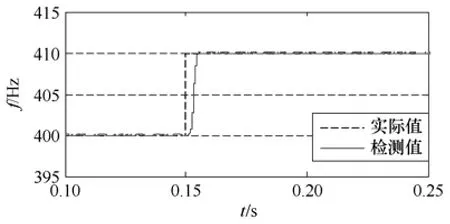
图4 三线DFT算法阶跃响应Fig.4 Step response of frequency estimation based on 3-line DFT

图5 为三线DFT算法的斜坡响应，电源的频率斜坡变化率为100Hz/s，初始频率为400Hz，在0.15s加斜坡信号。从图中可以看出，检测值对实际值的跟踪有延迟，该延迟约为6ms。产生延迟的原因是算法中需对长度为N的序列进行DFT，序列对变化信号的更新将有N个采样时间间隔的延迟。可见，减小参数N的选取不仅可以减小算法的计算量，同时可以减小频率检测的延迟时间，提高算法的响应带宽。

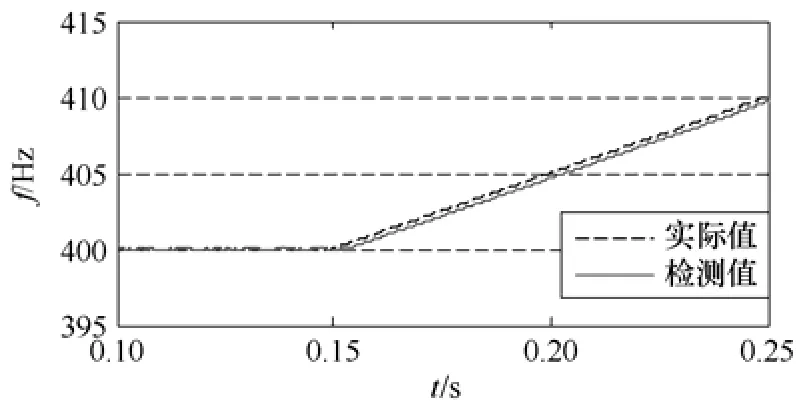
图5 三线DFT算法斜坡响应Fig.5 Ramp response of frequency estimation based on 3-line DFT

在电源参数设置相同的仿真条件下，对比PLL算法性能。PLL的仿真模型框图如图6所示。对电源的三相电压进行采样，采样频率为10kHz，经克拉克变换和帕克变换后，得到dq坐标下的电压矢量，设置q轴的参考值为零，经PI调节器和积分环节得到旋转矢量的角度，作为帕克变换的反馈量，实现对旋转矢量的相位跟踪。积分环节前端，即为频率量，经过低通滤波器后得到频率检测值。

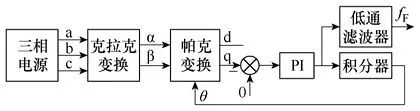
图6 PLL算法仿真模型框图Fig.6 Simulation diagram of PLL

图7 为PLL算法的阶跃响应，阶跃条件与图4相同。PLL算法的性能与PI参数的设置密切相关，图7中的PI设置，检测值无超调，响应时间约为12ms，存在明显的稳态误差，误差值约为±1Hz。产生稳态误差的原因为当仅存在基波矢量，q轴分量为零时，对应的d轴相位即为基波相位。但是如果存在谐波矢量，其旋转速度与基波不同，矢量合成后将影响q轴分量大小，q轴分量为零时对应的d轴相位与基波相位将有偏差。因此，PLL算法对谐波较为敏感。图8为PLL算法的斜坡响应，斜坡条件与图5相同。同样，受谐波分量影响，检测结果存在约±1Hz的误差。

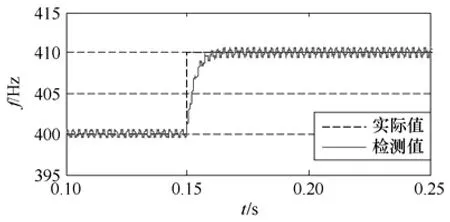
图7 PLL算法阶跃响应Fig.7 Step response of PLL

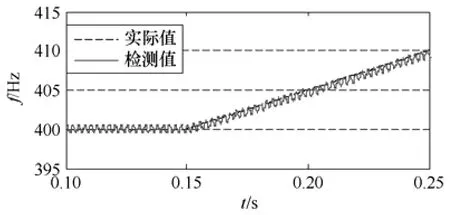
图8 PLL算法斜坡响应Fig.8 Ramp response of PLL

由仿真对比结果可以看出，三线DFT频率检测算法的阶跃响应和斜坡响应性能优于PLL算法，其具有较小的稳态误差和更快地阶跃响应性能。由于选择采样点数N时已保证基波与谐波主瓣互不重叠，可极大地减弱谐波对检测结果的影响，因此该算法对谐波干扰的抑制性较强。

4.2 实验验证

在双级矩阵变换器样机上对三线DFT算法进行验证。三相电压采样频率为5kHz，信号采样通道中低通滤波器的截止频率为2.1kHz，采样点数N为30，df为167Hz。采用的电压采样传感器为LV25-P，模-数转换芯片MAX1308为8路同时采样。在TMS320F2812 DSP芯片中实现三线DFT算法。

设定电源频率分别为360Hz、400Hz、500Hz和800Hz时，检测结果如图9中由下到上曲线所示。f0初始值为500Hz，算法根据检测频率范围不同进行步长为167Hz的迭代计算，对360～800Hz频率范围进行检测。从图9中可以看出，4组频率检测均有约4ms的响应时间。由于采样序列初始值为空，检测结果在开始阶段有波动。进入稳态后，在360Hz、400Hz和800Hz频率下，稳态误差均约为±0.5Hz，而500Hz频率下，稳态误差约为±0.3Hz。可见，如f0的选取与基波频率相同，A-1和A1幅值相等，可消除采样过程中的共模误差，检测结果会更加精确。

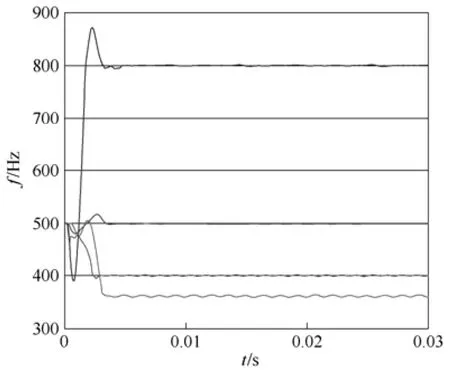
图9 4种频率下实验结果Fig.9 Experiment result of 4-frequency estimation

图10 为斜坡响应的检测结果，有约±0.5Hz纹波，延迟约为3ms。与仿真结果相比，采样点数N减小，延迟时间相应减小；实验稳态误差比仿真结果稍大，可以认为是由电压传感器采样误差等非理想因素造成。对比实验波形与仿真波形，结果基本一致。

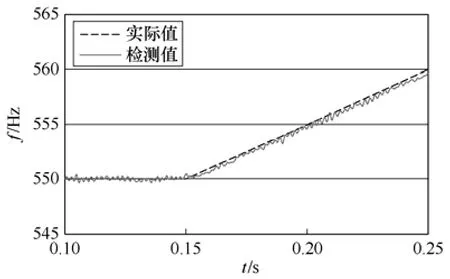
图10 斜坡频率实验结果Fig.10 Experiment result of ramp-frequency estimation

5 结论

（1）基于三线DFT的频率检测算法可实现对连续变化频率的实时检测，克服了栅栏效应。

（2）该算法采样点数少，采用旋转坐标法计算3个谱线幅值，与传统DFT相比，计算量小且实时性强。

（3）按照文中方法选择算法参数，无主瓣幅值泄露。迭代法估计频率初值，可检测360～800Hz频率。

（4）仿真和实验结果证明，该算法具有较高的动态性能和稳态精度。提高采样精度并减少计算舍弃误差，可使稳态精度得到进一步提高。

[1] Rosero J A,Ortega J A,Aldabas E,et al.Moving towards a more electric aircraft[J].IEEE Aerospace and Electronic Systems Magzine,2007,22(3): 3-9.

[2] Saleh S A,Rahman M A.Analysis and real-time testing of a controlled single-phase waveletmodulated inverter for capacitor-run induction motors[J].IEEE Transactions on Energy Conversion,2009,24(1): 21-29.

[3] Andreotti A,Bracale A,Caramia P,et al.Adaptive prony method for the calculation of power-quality indices in the presence of nonstationary disturbance waveforms[J].IEEE Transactions on Power Delivery,2009,24(2): 874-883.

[4] 丁屹峰,程浩忠,吕干云,等.基于Prony算法的谐波和间谐波频谱估计[J].电工技术学报,2005,20(10): 94-97.Ding Yifeng,Cheng Haozhong,Lu Ganyun,et al.Spectrum estimation of harmonics and interharmonics based on prony algorithm[J].Transactions of China Electrotechnical Society,2005,20(10): 94-97.

[5] Routray A,Pradhan A K,Rao K P.A novel kalman filter for frequency estimation of distorted signals in power systems[J].IEEE Transactions on Instrumentation and Measurement,2002,51(3): 469-479.

[6] Arruda N,Filho B J C,Silva S M,et al.Wide bandwidth single and three-phase PLL structures for grid-tied PV systems[C].28th IEEE Photovoltaic Specialist Conference,2000: 1660-1663.

[7] 龚锦霞,解大,张延迟.三相数字锁相环的原理及性能[J].电工技术学报,2009,24(10): 94-99.Gong Jinxia,Xie Da,Zhang Yanchi.Principle and performance of the three-phase digital phase-locked loop[J].Transactions of China Electrotechnical Society,2009,24(10): 94-99.

[8] McGrath B P,Holmes D G,Galloway J J H.Power converter line synchronization using a discrete fourier transform (DFT) based on a variable sample rate[J].IEEE Transactions on Power Electronics,2005,20(4):877-884.

[9] Thomas D W P,Woolfson M S.Evaluation of frequency tracking methods[J].IEEE Transactions on Power Delivery,2001,16(3): 367-371.

[10] Kia S H,Henao H,Capolino G A.A high-resolution frequency estimation method for three-phase induction machine fault detection[J].IEEE Transactions on Industrial Electronics,2007,54(4): 2305-2314.

[11] Mojiri M,Ghartemani M K,Bakhshai A.Estimation of power system frequency using an adaptive notch filter[J].IEEE Transactions on Instrumentation and Measurement,2007,56(6): 2470-2477.

[12] Andria G,Dell’Aquila A,Salvatore L.Analysis of distorted unbalanced waveforms in inverter drives[J].IEEE Transactions on Power Electronics,1989,4(2):298-310.