协调大规模风电汇聚外送的火电容量优化

侯婷婷 娄素华 张滋华 吴耀武

（华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074）

1 引言

随着全球性的传统化石能源枯竭、环境污染和气候变暖问题的日益突出，大力发展风电等可再生能源发电成为世界各国的重大战略选择[1-4]。根据国家能源局确定的千万千瓦级风电基地规划，我国将于2020年建成哈密、酒泉等七个千万千瓦级风电基地，这种大规模、高集中开发的风电都在负荷比较低的偏远地区，所以仅在开发当地电网进行风电消纳是不可能或者说不科学的。以酒泉风电基地为例，其2015年的风电装机容量将达到1 271万kW，根据甘肃电网的电源结构和用电需求特性，靠其自身电网是无法完全消纳的。而2020年，酒泉风电基地的风电装机容量将增加到2 000万kW，在当地电力系统进行消纳更加困难，这就决定了未来大规模风电基地风能汇聚外送的必然趋势[5]。

然而，由于风电具有波动性、能量密度低的特点，一般的风电场年等效满发利用小时都在2 000～3 000h之间。若输送通道只外送风电一类电能，就会产生风电输送率和通道利用率之间的矛盾。在风电出力较小的时段，会有大量的输电通道容量空间冗余，使得输电通道的作用得不到充分的发挥，而风电出力较大的时段则可能导致输电通道不能将风电全部送出。因此，风电独立外送将很难同时保证输电系统的利用效率和风电的送出率。同时，由于风电出力的波动性，输送电能的质量也无法得到保证。因此，为风电基地建设配套电源与风电协调送出，将输电通道输送风电空余的容量空间利用起来，既能充分利用输电通道，增加经济效益，又能改善输送的电能质量，保证输送电力的稳定。

文献[5]通过对大规模风电基地—酒泉风电基地出力特性的研究得出结论：火电是大容量风电功率调节的合理选择，建设一定规模的火电并与风电配套送出，能够有效地解决风电的消纳问题。所以，本文采用火电作为风电外送的配套电源。对于送出一定容量的风电，确定配套建设火电的容量规模，有效平衡输电通道的容量作用发挥和风电的送出率，是目前需要深入研究的问题。

目前，风电相关的研究大都集中于风电机组的动态仿真[6-8]、风电场可靠性建模[9-11]及含风电系统的短期优化调度[12-14]等几个方面，仅有少数学者对大容量风电的外送输电问题进行了初步的研究[15-17]。文献[15，16]提出了含风电的输电系统可靠性评估方法，文献[17]提出了一种风电场群汇聚外送输电通道容量的优化方法，针对风电外送问题取得了一定的研究成果。但是，在风电外送配套电源容量优化方面尚未见相关文献。

本文对输电通道输送风电后的空余容量空间（Spare Capacity of Transmission Line，STC）的时序特性进行了分析，并定义了持续STC曲线。基于持续STC曲线，建立了风电汇聚外送配套火电容量优化模型。该模型在风电优先外送的前提下，合理利用输电通道的空余容量输送火电，使输电经济效益最大化，模型考虑了输电线路、配套电源的费用及输送电量收益。应用本文提出的模型对一个测试系统进行了仿真计算和分析，结果证明了模型的有效性。

2 风电外送配套火电可行性分析

为大规模风电外送配套出力可控电源可以弥补其输出的波动性，提高输电通道的输电效率。电力系统具有调节能力的电源一般有火电、水电及抽水蓄能等，水电和抽水蓄能电站常常会受到地理位置的制约，而火电建设相对比较灵活，可根据大容量风电外送需求进行优化配置。目前，美国、欧洲和中国的主流超临界火电机组的主要性能指标[18]见下表。

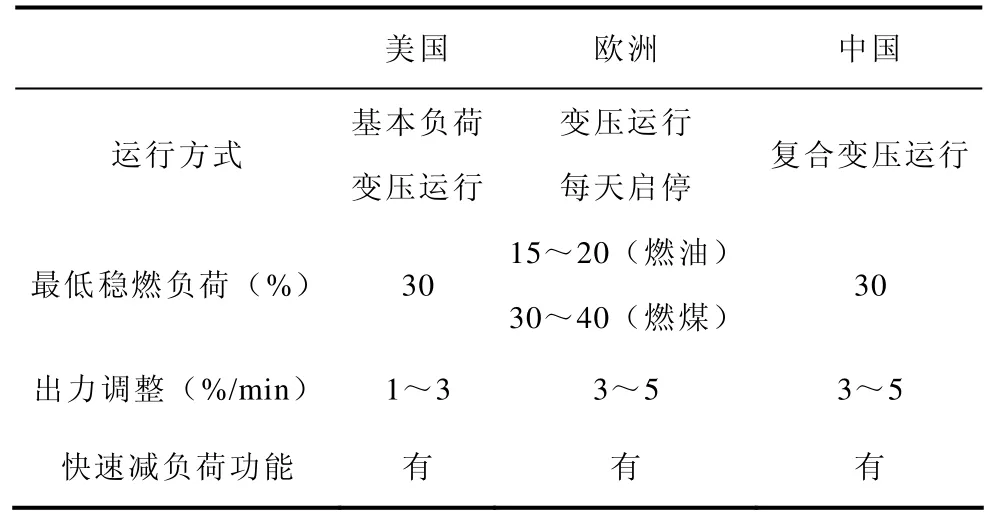
表 主流超临界火电机组性能指标Tab.Main supercritical thermal units’ performance indices

目前，国内外超临界燃煤火电机组的基本调峰深度可达50%，若采用投油调峰方式，其调峰深度可以上升至60%；出力调整速率可达到0.03～0.05MCR/min。根据对我国大型风电场群风电出力特性的研究分析[5]，临近多个风电场功率汇聚后其出力波动性大大抵消，变化率在0.015MCR/min以下的概率为99%，因此，采用火电调节风电功率的波动性是可行的。

3 输电通道火电可用容量持续曲线

大容量风电外送若取得输电效益的最大化，就要合理利用输电通道输送风电后空余的容量空间，为之配套合理容量的火电电源，既充分利用了输电通道的容量，同时又使因输电通道阻塞而不能完全送出的风电电量最小化。因此，分析输电通道输送风电后空余的容量空间特性十分关键。

3.1 输电通道的STC时序特性

STC定义为：按照既定的送电协议，优先输送风电电力后剩余的容量空间。

t时刻STC的数学表达式如下：

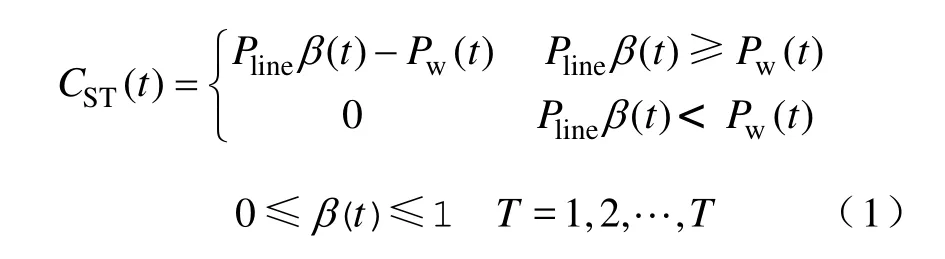
式中，Pline、β(t)及Pw(t)分别为输电通道容量、t时刻协议送电功率与输电通道容量的比值及多个风电场汇聚后的出力；T为运行周期的总时段数；β(t)反映了电能外送的送电曲线特性，在实际运行中是根据不同的目的由送、受端协议确定。当β(t)恒为1时，代表输电通道全年满送；当考虑受端系统的调峰压力时，β(t)可根据受端系统的负荷特性确定。

图1为送电协议为输电通道全年满送时，即β(t)=1，t=1,2,…,T，对应的某一风电基地连续一周的出力曲线及相应的STC时序曲线，输电通道容量为750万kW，外送风电总容量为750万kW。由此图可以看出，STC曲线保留了风电出力的随机性和波动性，同时，与风电出力大小具有互补性。

图1 风电出力和对应STC时序曲线Fig.1 Sequential curve of wind power output of a wind base and its corresponding STC

3.2 输电通道的持续STC曲线

由于风电预测的短期特性，无法对未来规划年的风电出力曲线进行精确预测，所以若采用风电出力时序曲线及时序STC曲线进行未来几年后的风火协调外送分析是极其困难的。对于一个特定地区，其每年的风能资源不会变化太大，具有相似的概率分布特性。故本文借鉴持续负荷曲线的概念，基于风电出力的历史数据，研究通道输送风电后空余容量的概率分布特性，建立输电通道的持续STC曲线。

对风电场的历史出力数据和输电通道的送电协议统计分析后可得到STC的累积概率分布曲线，图2所示的为送电协议比恒为1时的STC累积概率分布曲线。

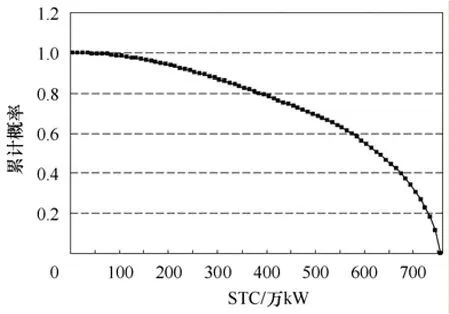
图2 STC累积概率分布曲线Fig.2 Cumulative probability distribution curve of STC

对于图2中任意一点（STC0，p(STC0)），表示STC大于或者等于STC0的概率为p(STC0)，即

两端乘以T，可得STC大于或者等于STC0的持续时间：

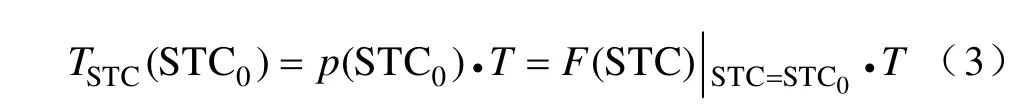
TSTC(STC)即由STC的累积概率曲线转化为的持续STC曲线。式中，F(STC)、f(STC)分别为STC的累积概率分布函数和概率密度函数。

在配套火电容量优化中，输电通道输送风电后剩余的容量空间即为配套火电可用的通道容量，因此，持续STC曲线可看作火电所能承担的最大等效持续负荷曲线。

在实际应用中，根据输送通道的送电曲线和风电出力曲线可以得到STC曲线，而输电通道的曲线则由送电和受电双方根据受端系统负荷特性和电源调节特性协调确定。

4 风电外送配套火电容量优化模型

4.1 目标函数

火电与风电协调外送的目标一方面是要充分送出可再生的风电资源，另一方面是获得输电效益的最大化，其模型目标函数为

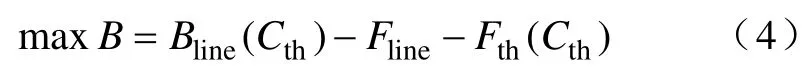
式中，B表示风电与火电协调外送总的净收益；Bline表示通道输送的年电量收益，包括输送的风电电量收益Bw和火电电量收益Bth两部分；Cth为配套火电的容量；Fline表示输电通道的投资等年值和固定运行费；Fth表示配套火电的年总费用，由投资等年值、固定运行费用和可变运行费用三部分组成[19]。

Fline和Fth的表达式分别为

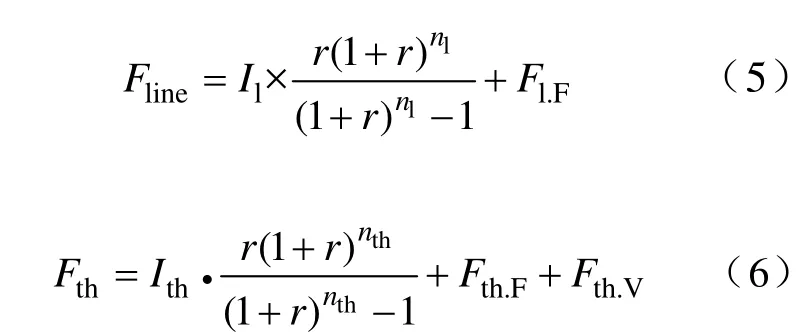
式中，Il和Fl.F分别为输电线路总投资和年固定运行维护费；Ith、Fth.F和Fth.V分别为配套火电总投资、年固定运行维护费和可变运行费；nl、nth分别为输电线路和配套火电的寿命；r为贴现率（%）。

4.2 约束条件

风电外送配套火电容量优化模型的约束条件包括输电线路容量约束、火电机组运行约束和风电场运行约束三部分。

（1）输电通道送电容量约束。即任何时候，输电通道输送的风电和火电电力不超过协议送电容量：

式中，Pline、Pth(t)、Pw(t)分别为输电通道容量、输电通道在t时刻输送的火电电力和风电电力。

（2）火电机组约束

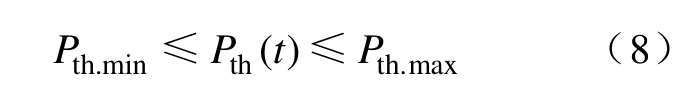
式中，Pth.min、Pth.max分别为机组最小、最大出力。

（3）风电场运行约束

①风电场出力约束，即风电场的出力不大于风电场装机总容量：

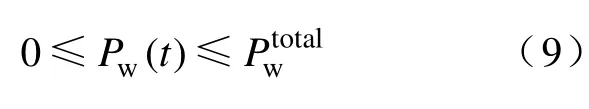
②风电场电量约束，即送出风电场发电量和未送出的电量之和等于风电场期望发电量：

式中，tE为风电场的年期望利用小时；EW、EENAW分别为输电通道送出和未送出的风电电量。

4.3 配套火电容量优化原理

本文建立的风火联合外送模型是一个两层优化问题，上层是优化配套火电的总容量。下层是对于某一配套火电容量。基于持续STC曲线优化送出火电的送电曲线，使得火电运行的经济性最优，优化原理如图3所示。

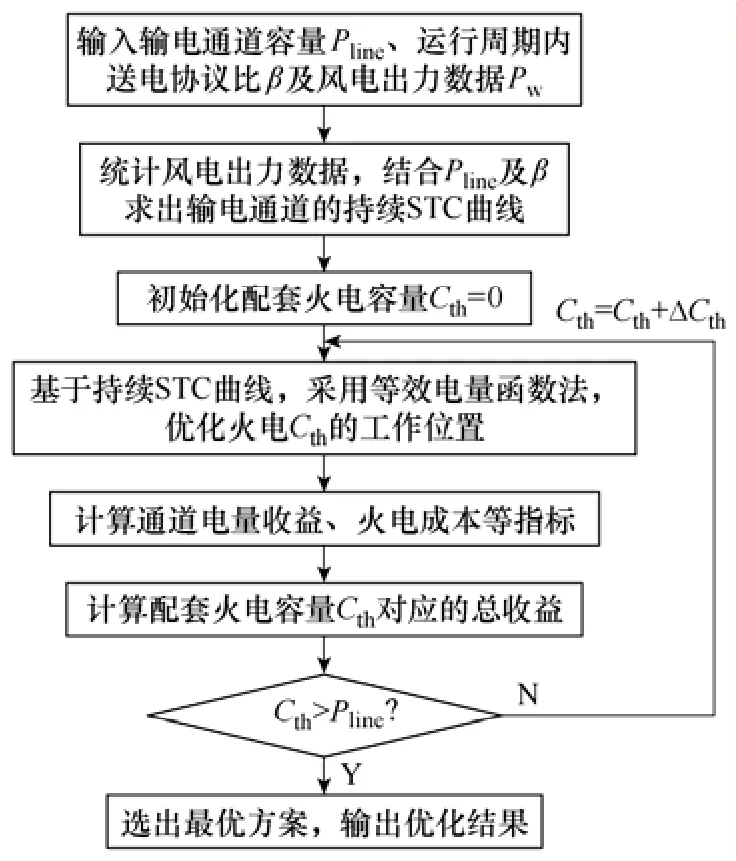
图3 风电外送配套火电容量优化原理框图Fig.3 Flowchart of capacity optimization of corollary thermal sources transmitted with wind power together

5 算例分析

采用本文提出的协调风电外送配套火电容量优化方法，对2015年西部某风电基地的风火联合外送至中部地区的问题进行了计算分析。

本算例中，输电通道容量和外送风电额定容量均为已知（采用规划水平），分别为：750万kW和750万kW。基于我国目前新建火电机组的情况，选择单机容量为60万kW的火电机组作为配套火电，其实际平均发电煤耗为300g/kW·h，根据电监会公布的《2007、2008年投产电力工程项目造价情况通报》[20]，火电的单位投资和寿命分别取4 000元/kW和25年，标煤煤价为650元/t，根据发改委公布的火电上网电价[21]，电价取为0.35元/kWh，贴现率r为0.1。

考虑受端系统的负荷特性和输电通道的实际利用效率，协议送电曲线拟定为：受端系统负荷低谷时段送电协议比β(t)为0.5，高峰负荷时段送电协议比β(t)为1，腰荷时段的送电协议比β(t)为0.83，输电通道年综合送电利用小时数为6 800。

5.1 持续STC曲线

对风电出力的历史数据进行统计分析，并结合输电通道容量及送电协议，得到风电外送通道的持续STC曲线如图4所示。

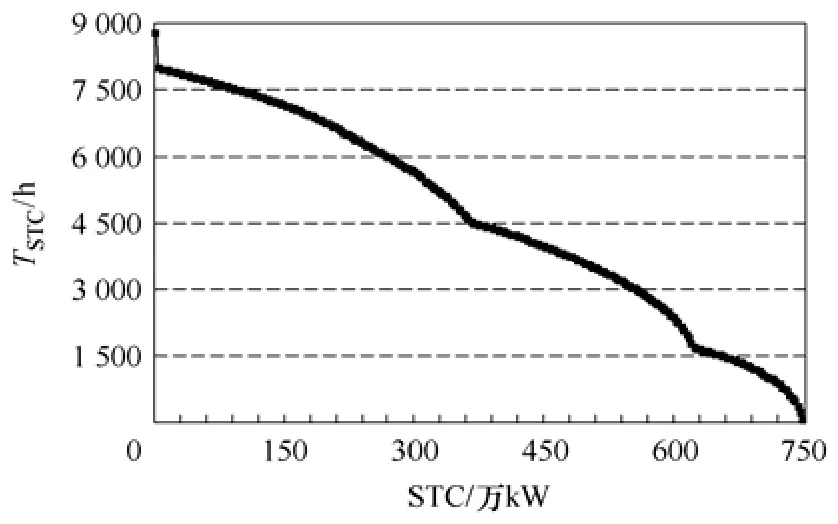
图4 持续STC曲线Fig.4 Duration curve of STC

由图4看出，750万kW的输电通道按照既定送电协议送总容量750万kW的风电之后，还有较大的通道容量空间没有利用，STC大于440万kW的时间达到了4000h。由此可见，由于风电资源的特性，外送输电通道输送风电之后会有大量的空余容量空间，为充分利用输电通道，有必要建设一定容量的配套电源与风电协调送出。

由于输电通道按照受端负荷特性分三个水平来输送电力，该送电协议下的持续STC曲线是一条非持续光滑的连续曲线，由三段持续光滑的曲线组成。也就是说，持续STC的特性是与送电曲线的形状是密切相关的。

5.2 风电外送配套火电容量优化结果

基于持续STC曲线，采用本文提出的模型对不同火电配套容量方案进行了计算，图5 给出了不同火电配套容量时的风电外送总的净收益。

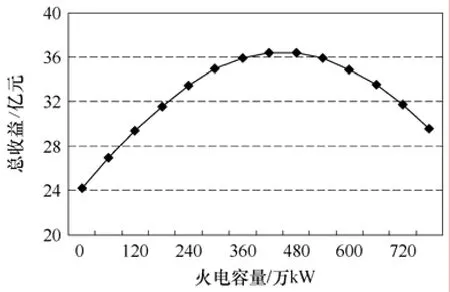
图5 不同配套火电容量时的总收益Fig.5 Benefits of schemes with different corollary thermal source capacities

从图5可看出，在配套火电容量较小时，随着配套火电容量的增大，输电通道利用越充分，输电通道收益即随之增加。而当配套火电容量增大到一定程度后，即增加的火电投资以及固定运行费用与增加的火电送出电能收益相平衡时，获得最佳的风火协调外送总收益；此后，如果继续增加的配套火电容量，因受输电通道输送能力的限制，配套火电发电小时数下降，则总收益会随着配套火电容量的增加而降低。对于文中的测试系统，采用60万kW火电机组进行配套外送，其最优配套容量为480万kW，输电总收益为36.42亿元，比单纯送风电的净收益增加了12.26亿元，增幅达到50.7%。

5.3 电价影响分析

落地电价是风火联合外送效益的一个重要影响因素。采用文中模型，对不同落地电价对应的最优配套火电容量及输电收益进行了计算，结果如图6所示。

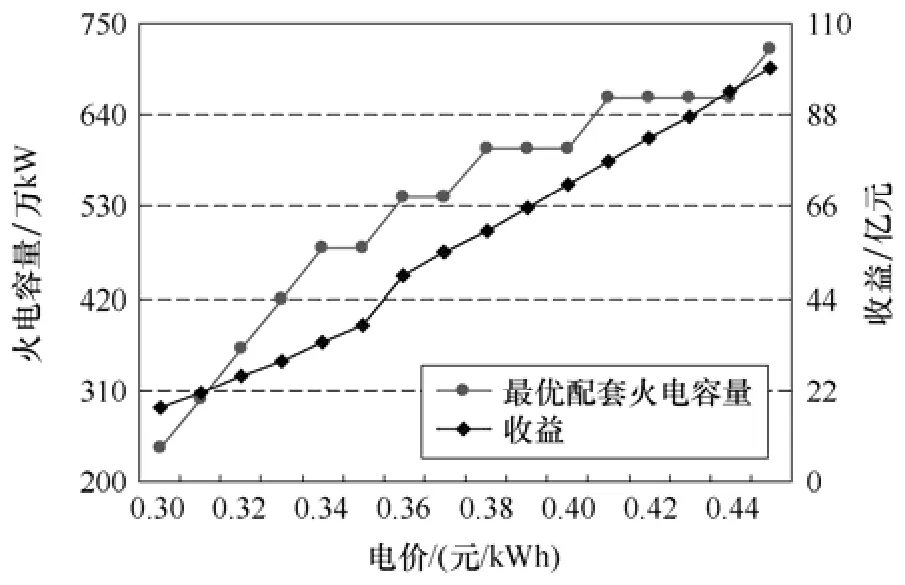
图6 不同落地电价时的优化方案结果Fig.6 Optimal results under different electricity price

图6 给出了不同落地电价时的风电外送配套火电最优容量及对应的输电收益，从图中可以看出，落地电价对配套火电的最佳容量有很大的影响，在电价的增长初期，配套火电的最佳容量迅速上升，经过一段急速上升期之后，随着电价的增长，最佳配套火电容量的增加逐步变缓。这是因为，高的落地电价会增加送电的收益，促使输电通道多输送电量，充分利用输电通道空闲的输送能力，进而获取更大的经济效益。在电价增长初期，较多的STC空间使得配套火电最佳容量迅速增大，之后由于受输电通道容量的限制，增加的单位火电投资获得收益减少，从而抑制配套火电容量的增加速度。

5.4 火电煤价影响分析

火电机组的燃料价格是影响与风电配套送出火电容量规模的另一重要因素。采用本文模型，对不同火电煤价对应的最优配套火电容量及净收益进行了计算，结果如图7所示。

图7 不同火电煤价时的优化方案结果Fig.7 Optimal results under different coal price

由图7可知，随着火电煤价的增大，输送相同电量获得的收入不变，而成本却增大，输电通道输电的净收益是减小的，因此促使配套火电的最优容量也呈逐渐降低的趋势。火电煤价为500元/t时，最优配套火电容量高达600万kW；而火电煤价为800元/t时，若送电的落地电价不变，最优的配套火电容量仅为300万kW。因此，风电外送配套火电的建设需要对其一次能源合理的进行评估。

6 结论

随着我国风电的大规模、高集中开发，大容量风电远距离外送成为解决风电消纳问题的一个有效手段。由于风电资源本身的年利用小时数较低，为其建设一定容量的配套电源联合送出才能保证风电外送的综合效益。本文针对风电外送配套火电容量优化问题，提出了一种解决思路。基于风电出力的历史数据，定义了输电通道火电可用容量空间的持续曲线，即STC持续曲线，进而建立了风电外送配套火电容量优化模型，通过对算例系统的计算及结果分析可以得到以下结论：

（1）由于风电资源特点，输电通道输送风电之后会有大量的空余容量空间，配套火电与风电协调外送可以大大提高输电综合效益。

（2）落地电价和火电煤价均会对风电外送配套火电的最优容量和输电效益产生影响。

（3）未来风电外送配套火电容量的确定需综合考虑多方面的因素，包括火电煤价、风电出力特性、落地电价等。

本文提出的模型和方法能够为未来我国大规模风电基地的风电外送配套电源容量的优化及风电外送综合效益评估提供一定的指导。

[1] Valenzuela Jorge,Wang Jianhui.A probabilistic model for assessing the long-term economics of wind energy[J].Electric Power Systems Research,2011,81(4): 853-861.

[2] Siahkali H,Vakilian M.Stochastic unit commitment of wind farms integrated in power system[J].Electric Power Systems Research,2010,80(9): 1006-1017.

[3] 邓卫,唐西胜,裴玮,等.含风电微型电网电压稳定性分析及控制技术[J].电工技术学报,2012,27(1): 56-62.Deng Wei,Tang Xisheng,Pei Wei,et al.Voltage stability and control technologies of micro-grid with wind power[J].Transactions of China Electrotechnical Society,2012,27(1): 56-62.

[4] 尹明,王成山,葛旭波,等.中德风电发展的比较与分析[J].电工技术学报,2010,25(9): 157-163.Yin Ming,Wang Chengshan,Ge Xubo,et al.Comparison and analysis of wind power development between China and Germany[J].Transactions of China Electrotechnical Society,2010,25(9): 157-163.

[5] 肖创英,汪宁渤,丁坤,等.甘肃酒泉风电功率调节方式的研究[J].中国电机工程学报,2010,30(10):1-7.Xiao Chuangying,Wang Ningbo,Ding Kun,et al.System power regulation scheme for Jiuquan wind power base[J].Proceedings of the CSEE,2010,30(10): 1-7.

[6] 李东东,陈陈.风力发电机组动态模型研究[J].中国电机工程学报,2005,25(3): 115-119.Li Dongdong,Chen Chen.A study on dynamic model of wind turbine generator sets[J].Proceedings of the CSEE,2005,25(3): 115-119.

[7] 高峰,周孝信,朱宁辉,等.直驱式风电机组机电暂态建模及仿真[J].电网技术,2011,35(11): 29-34.Gao Feng,Zhou Xiaoxin,Zhu Ninghui,et al.Electromechanical transient modeling and simulation of direct-drive wind turbine system with permanent magnet synchronous generator[J].Power System Technology,2011,35(11): 29-34.

[8] 张帆,李国庆,张宇阳,等.双馈感应风电机组建模控制仿真[J].东北电力大学学报,2011,31(4):80-85.Zhang Fan,Li Guoqing,Zhang Yuyang,et al.Modeling control and simulate of DFIG wind generator[J].Journal of Northeast Dianli University,2011,31(4): 80-85.

[9] Francois Valler,Jacques Lobry,Olivier Deblecker.System reliability assessment method for wind power integration[J].IEEE Transactions on Power Systems,2008,23(3): 1288-1297.

[10] Y Gao,R Billonton.Adequacy assessment of generating systems containing wind power considering wind speed correlation[J].IET Renewable Power Generation,2009,3 (2): 217-226.

[11] 李玉敦,谢开贵.含多个风电场的电力系统可靠性评估[J].电力科学与技术学报,2011,26(1): 73-77.Li Yudun,Xie Kaigui.Reliability assessment of power systems containing multiple wind farms[J].Journal of Electric Power Science and Technology,2011,26 (1): 73-77.

[12] Francois Bouffard,Francisco D Galiana.Stochastic security for operations planning with sugnificant wind power generation[J].IEEE Transactions on Power Systems,2008,23 (2): 306-316.

[13] Aidan Tuohu,Peter Meibom,Eleanor Denny,et al.Unit commitment for systems with signicant wind penetration[J].IEEE Transactions on Power Systems,2009,24 (2): 592-601.

[14] 江岳文,陈冲,温步瀛.含风电场的电力系统机组组合问题随机模拟粒子群算法[J].电工技术学报,2009,24 (6): 129-137.Jiang Yuewen,Chen Chong,Wen Buying.Particle swarm research of stochatic simulation for unit commitment in wind farms integrated power system[J].Transactions of China Electrotechnical Society,2009,24(6):129-137.

[15] Billinton R,Wangdee M.Reliability-based transmission reinforcement planning associated with large-scale wind farms[J].IEEE Transactions on Power Systems,2007,22(1): 34-41.

[16] 吴义纯,丁明,李生虎.风电场对发输电系统可靠性影响的评估[J].电工技术学报,2004,19(11):72-76.Wu Yichun,Ding Ming,Li Shenghu.Reliability assessment of wind farms in generation and transmission systems[J].Transactions of China Electrotechnical Society,2004,19(11):72-76.

[17] 穆钢,崔杨,严干贵.确定风电场群功率汇聚外送输电容量的静态综合优化方法[J].中国电机工程学报,2011,31(1): 15-19.Mu Gang,Cui Yang,Yan Gangui.A static optimation method to determine integrated power transmission capacity of clustering wind farms[J].Proceedings of the CSEE,2011,31 (1): 15-19.

[18] 刘凯.超临界汽轮机组的发展及关键技术（二）[J].江苏电机工程,2005,24 (2): 21-25.Liu Kai.Development and key technology of supercritical steam turbine unit[J].Jiangsu Electrical Engineering,2005,24 (2): 21-25.

[19] WU Yaowu,Lou Suhua,Lu Siyu.A model for power system interconnection planning under low-carbon economy with CO2emission constraints[J].IEEE Transactions on Sustainable Energy,2011,2(3): 205-214.

[20] http://www.serc.gov.cn/zwgk/jggg/201111/t20111128_15602.htm.

[21] http://www.sdpc.gov.cn/zfdj/default.htm.