变频器驱动下组合转子电机运行性能

陈学珍 辜承林

（1.黄石理工学院电气与电子工程学院 黄石 435003 2.华中科技大学电气与电子工程学院 武汉 430074）

1 引言

高密度轴向叠片各向异性(ALA) 转子电机的定子与普通电机的定子相同，转子由高导磁材料和非导磁绝缘材料叠片沿轴向交替高密叠压而成，是一种具有高凸极比(Ldr/Lqr)[1,2]的同步磁阻电机。永磁同步电机具有高转矩密度、高效率、高功率因数的优点，ALA转子与永磁转子组合，有可能获得更好的运行性能[3-7]。组合转子电机虽兼有上述两种电机的优点，但它们的转子上都没有阻尼绕阻，逆变器供电开环空载起动仍有可能出现振荡现象。文献[8]利用小信号扰动法研究了磁阻电机参数对电机稳定性的影响。文献[9]用小信号模型分析了ALA转子电机开环V/f控制振荡的原因。文献[10]指出ALA转子电机的稳定性与电机特定的结构和供电电源有关。文献[11]研究了惯性阻尼器的粘滞阻尼转矩系数和阻尼器的转动惯量对步进电机阶跃响应的影响。文献[12]研究了惯性阻尼器对组合式转子电机变频器供电空载起动性能的影响。文献[13]以弱磁扩速比和最大电磁转矩为评价指标，探讨了组合转子电机的综合性能提高的基本设计规律。至今为止，报道这种组合转子电机变频起动振荡的原因和负载能力的文献还比较少见。

为此，本文从4极组合转子样机变频器供电开环空载起动的实验现象出发，用小信号模型分析了产生振荡的原因和在转子轴上附加机械惯性阻尼器后电机的抗扰动能力，实验验证了理论分析的结果。图1是4极组合转子截面图，图2是4极组合式转子样机。

图1 4极组合转子截面图Fig.1 Cross-section of 4-pole hybrid rotor

图2 4极组合转子样机Fig.2 4-pole hybrid rotor prototype

2 样机实验现象

实验样机的基本参数：额定功率PN= 2.2kW，额定相电压UN=220V，直轴电感Ld=108.8mH，交轴电感Lq=48.6mH，额定频率fN=50Hz，极对数p=2，永磁磁链幅值ψm=0.48V/(rad/s)。

实验使用Panasonic公司的M1X374BSA通用变频器供电，设置恒压频比V/f控制，输出SPWM调制波，三角载波频率为8kHz。通过变频器操作面上的控制键来实现电机的加/减速、起/停及复位功能。手动升频的实验记录见表1。表1中，f为设定变频器输出频率，n0为对应的同步转速，n为实测转速，Iu为相电流。

表1 变频器供电下4极组合转子电机空载起动实验记录Tab.1 Starting data of the 4-pole combined rotor machine by inverter supply under no-load

可见，随着电源频率的升高，电机振荡越来越剧烈，最终导致变频器限流保护。

3 振荡原因分析

3.1 小信号数学模型

电机振荡一般分为同步振荡和异步振荡两种类型：同步振荡在振荡过程中振幅逐渐衰减，最终达到新的平衡位置进入稳定运行状态；异步振荡在振荡过程中振幅越来越大，最终导致失步[15]。本文主要用小信号模型分析电机异步振荡的原因，为简便计算和分析，假设：①不考虑饱和影响；②SPM段各向同性；③忽略SPM段与ALA段之间的漏磁影响。设有恒定幅值振荡的小扰动作用于稳态运行的电动机上，转子位置的微小增量可近似用如下函数表示[9]

式中 Δθm——转子位置小扰动的振幅；

α——电机振荡角频率。

转子位置角为

式中，下标“0”为稳态值。

由永磁体产生的磁链为[14]

式中ψm——永磁体产生的磁链幅值。

转子角速度为

组合转子电机电压方程为

小扰动d、q轴电流可表示为

将式（1）～式（4）和式（6）代入式（5），可求得正弦稳态下的电流小扰动分量Δid和Δiq。

电机的电磁转矩经线性化后，得

式（7）中电磁转矩的波动分量ΔTe计算，忽略其二阶部分，同时考虑cosΔθ≈1，sinΔθ≈Δθ，可得

将Δid和Δiq代入式（8）得

式中ks——同步转矩系数；

kd——电磁阻尼转矩系数，且

式中，ΔId′和ΔIq′分别为

3.2 电磁阻尼转矩系数对系统稳定性影响

转子的运动方程为

式中J——电机的转动惯量；

kB——机械粘滞阻尼系数。

式（11）线性化后，并将式（1）、式（7）和式（9）代入，得到描述动态不稳定的联立方程[14]

从式（11）可看出，电机系统的稳定是由机械粘滞阻尼系数和电磁阻尼系数共同决定的。只有kB+kd＞0时，振荡幅值衰减，系统才可能稳定；kB+kd=0时，等幅振荡；kB+kd＜0时，振荡幅值增大，后两种情况系统都不稳定。由式（5）电压稳态方程、式（9）和式（13）联立可求得给定频率对应的电磁阻尼系数kd。

图3为空载时电磁阻尼系数kd与频率的关系，kd随频率升高从正电磁阻尼（系统稳定）减小到负电磁阻尼最小值（电机振荡最剧烈），然后有回升趋势（振荡减缓），表明电机振荡是在某个频率区出现了负电磁阻尼，抗扰动能力差。

图3 电磁阻尼系数kd与运行频率f的关系Fig.3 Electromagnet damper factor kd versus frequency f

4 运行性能分析

为了解决振荡问题，本课题组提出了在转子轴上直接安装机械惯性阻尼器，用增加的机械粘性阻尼系数来补偿负电磁阻尼系数。本文主要分析额定频率点50Hz处机械惯性阻尼器粘性阻尼系数Tdd和惯量盘惯量Jd与组合转子电机负载运行性能的关系。转子轴上附加机械惯性阻尼器后的转子小信号动态模型的状态变换矩阵A(x) 为[12]。

变量x的小扰动矩阵Δx为[12]

式中ωd——惯量盘的角速度。

根据线性系统稳定理论，若A(x) 的所有特征值的实部为负值，则系统在所给定的运行条件下是稳定的，否则为不稳定。

图4为无惯性阻尼器，不同负载TLA(x) 主导特征值轨迹。电机在轻载和TL＞16N·m时不稳定。图5为Jd=0.02时，不同负载TL不同TddA(x) 主导特征值轨迹，电机在TL＜29N·m范围内都能稳定运行。可见，附加惯性阻尼器后，提高了负载能力，而且从图5可看出，选择合适的Tdd可以得到最佳的稳定性。图6为Tdd=0.2时，不同负载TL不同JdA(x)主导特征值轨迹，Jd过小系统稳定性下降；Jd过大，主导特征值由复极点向实极点转移，动态性能变差，因此合适的Jd可提高系统稳定性和动态性能。综合上述，转子轴上附加合适的惯性阻尼器能提高电机抗扰动能力和负载性能，分析结果为后续的实验提供理论依据。

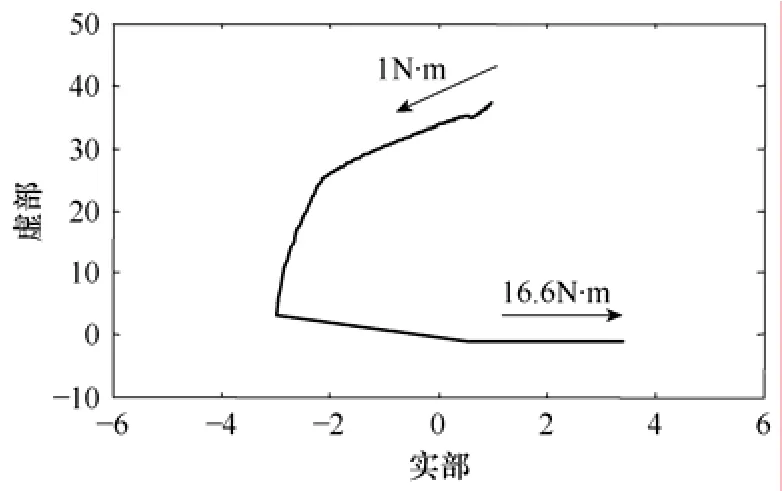
图4 不同负载TLA(x) 主导特征值轨迹（未加惯性阻尼器）Fig.4 Loci of the A(x) dominant eigenvalues under different load conditions (without damper)

图5 Jd=0.02时，不同负载TL不同Tdd A(x) 主导特征值轨迹Fig.5 Loci of the A(x) dominant eigenvalues under different load conditions with the different Tdd (Jd=0.02)

图6 Tdd=0.2时，不同负载TL不同JdA(x)主导特征值轨迹Fig.6 Loci of the A(x) dominant eigenvalues under different load conditions with the different Jd(Tdd =0.2)

5 附加惯性阻尼器后的样机实验

5.1 变频器供电起动实验

机械惯性阻尼器安装在组合转子电机非输出端轴上，另一端与测速发电机同轴连接，示波器与发电机输出端连接。变频器设定为自动升频方式，调节机械阻尼器的阻尼大小，得到电机从零频升到额定频率过程的速度曲线如图7所示。可见，随着变频器输出频率的升高，电机基本不振荡，能同步升速到额定转速稳定运行。表明机械惯性阻尼器明显改善了组合转子电机的变频起动性能。

图7 组合转子电机速度曲线Fig.7 Speed curve of the combined rotor machine

5.2 负载性能实验

图8 为组合转子电机负载性能实验示意图，带阻尼器的组合转子电机拖动直流电机带负载运行，通过调节滑动变阻箱来改变负载大小。发电机输出功率通过直流电压表和电流表测量负载电压U和电流I获得。

图8 组合转子电机负载性能实验示意图Fig.8 Load performance test diagram of combined rotor machine

组合转子电机的电磁功率Pem计算式为[9]

式中Ra——直流电机电枢电阻；

Ωr——机械角速度；

T0——机组的空载转矩。T0表达式为

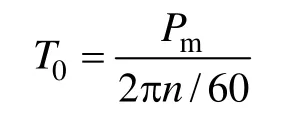
在负载性能实验之前，将直流电机拖动组合转子电机到某个转速空载运行，测量直流电机的电枢电压和电流得到机组的空载功率，减去直流电机铜损，即得该转速下机组的机械功率Pm[9]。

表2为加惯性阻尼器的组合转子电机负载性能实验数据，表中Pem和P*em分别为加阻尼器和未加阻尼器的电机的电磁功率。由于电机未加阻尼器只能在低速运行，为了更好地比较加阻尼器前后的负载性能，因此只给出了低速运行的实验结果。由表中数据可见，加阻尼器后的电机可承受更大的负载扰动，负载能力显著提高了。

表2 加惯性阻尼器的组合转子电机负载性能实验结果Tab.2 Load performance data of the combined rotormachine with damper

6 结论

本文通过对组合转子同步电机小信号模型分析及实验研究，得到如下结论：

（1）负电磁阻尼系数是组合转子电机变频器供电开环运行出现振荡的主要原因。

（2）转子轴上附加合适的机械惯性阻尼器是改善电机系统运行性能的最简单、经济又有效可行的方法。

[1] Nicola Bianchi,Chalmers Brian J.Axially laminated reluctance motor: analytical and finite-element methods for magnetic analysis[J].IEEE Transactions on Magnetics,2002,38(1): 239-245.

[2] 郭伟,赵争鸣.新型同步磁阻永磁电机的结构与电磁参数关系分析[J].中国电机工程学报,2005,25(11): 124-128.Guo Wei,Zhao Zhengming.Analysis of the relation between the electro-magnetic parameter and the structure of synchronous reluctance permanent magnetic motors[J].Proceedings of the CSEE,2005,25(11): 124-128.

[3] 吴志峤,辜承林.新型组合式转子同步电机参数研究[J].电机与控制学报,2002,6(1): 10-13.Wu Zhiqiao,Gu Chenglin.Research on parameters of synchronous machine with two-part rotor[J].Electric Machines and Control,2002,6(1): 10-13.

[4] 严岚.永磁无刷直流电机弱磁技术研究[D].杭州:浙江大学,2004.

[5] 赵宇,宁圃奇,柴建云.新型复合转子永磁磁阻电机设计[J].电机与控制应用,2007,34(1): 7-10.Zhao Yu,Ning Puqi,Chai Jianyun.Design of the combined PM-reluctance motors[J].Electric Machines & Control Application,2007,34(1): 7-10.

[6] Shigeo Morimoto,Masayuki Sanada,Yoji Takeda.Performance of PM-assisted synchronous reluctance motor for high-efficiency and wide constant-power operation[J].IEEE Transactions on Industry Applications,2001,37(5): 1234-1239.

[7] Ion Boldea,Lucian Tutelea,Cristian Ilie Pitic.PM-assisted reluctance synchronous motor/generator(PM-RSM)for mild hybrid vehicles: electromagnetic design[J].IEEE Transactions on Industry Applications,2004,40(2): 492-498.

[8] Honsinger V B,Steady state performance of reluctance machine[J].IEEE Transactions on Power Apparatus and Syatems,1971,PAS-90: 305-311.

[9] 朱建华,辜承林.变频器驱动下ALA转子电机运行性能的实验研究[J].微特电机,2007,35(7): 1-3,7.Zhu Jianhua,Gu Chenglin.Experimental Research on operating performance of ALA rotor motor driven by VVVF inverter[J].Small & Special Electrical Machines,2007,35(7): 1-3,7.

[10] 吴志峤,辜承林.ALA转子电机稳定性研究[J].电机与控制学报,2003,7(3): 182-186.Wu Zhiqiao,Gu Chenglin.Research on stability of ALA rotor machine [J].Electric Machines and Control,2003,7(3): 182-186.

[11] Lawrenson P J,Kingham I E.Viscously coupled inertial damping of stepping motor[J].Proceedings IEE,1975,122(10): 1137-1140.

[12] 陈学珍,辜承林.组合转子同步电机稳定性探讨[J].电机与控制学报,2010,14(12): 41-46.Chen Xuezhen,Gu Chenglin.Research on stability of hybrid rotor synchronous machine[J].Electric Machines and Control,2010,14(12): 41-46.

[13] 陈学珍,辜承林.ALA+SPM组合转子同步电机设计探讨[J].中国电机工程学报,2010,30(21): 98-102.Chen Xuezhen,Gu Chenglin.Design research on ALA+SPM rotor synchronous machine[J].Proceedings of the CSEE,2010,30(21): 98-102.

[14] 谷爱昱,陆永平.脉振磁场永磁低速同步电动机的稳定性分析[J].中小型电机,2003,30(1): 21-23.Gu Aiyu,Lu Yongping.Analysis of stability for pulsating magnetic field PM low speed synchronous motor[J].S&M Electric Machines,2003,30(1):21-23.

[15] Chen Xuezhen,Gu Chenglin.Research on operating performance for hybrid rotor synchronous motor[J].Electronics and Electrical Engineering,2011,113(7):3-8.