失谐多级整体叶盘振动模态特性定量评价方法研究

葛长闯，王建军，刘永泉

（1.中航工业沈阳发动机设计研究所，沈阳 110015；2.北京航空航天大学能源与动力工程学院，北京 100191）

失谐多级整体叶盘振动模态特性定量评价方法研究

葛长闯1，王建军2，刘永泉1

（1.中航工业沈阳发动机设计研究所，沈阳 110015；2.北京航空航天大学能源与动力工程学院，北京 100191）

主要研究了失谐多级叶盘振动模态局部化的定量评价方法。采用3种基于应变能理论的模态局部化因子来，评价失谐多级叶盘的振动模态特性。在此基础上，分析了典型失谐模式的2级叶盘模态局部化特性。分析结果表明：3种模态局部化因子在失谐多级叶盘振动评价中具有较好的适应性。

失谐；多级叶盘；模态；定量评价；应变能；局部化因子

0 引言

涡轮发动机叶盘结构通常被认为是周期对称结构，由于受制造误差、材料性质、使用磨损或为抑制颤振对叶片进行错频等因素的影响，造成实际叶盘各扇区间有小量差别，这种叶盘通常称为失谐叶盘。失谐叶盘工作时往往会出现1个或少数几个扇区振动较大而其余扇区振动不明显的现象，从而造成局部率先疲劳失效。这一现象在刚性较弱的叶片结构上反映明显，在工程上通常将这种叶片称为“傻子叶片”或“强盗叶片”[1]。国内外对失谐叶盘的研究主要集中于对单级叶盘振动特性研究，获得了一些经验和评价方法[1-2]；对于失谐多级叶盘振动特性及分析评价方法的研究开展得较少[3-5]，国内尚未看到公开研究资料。

本文开展失谐多级叶盘失谐特性的定量评价方法研究，并利用其方法分析了多级失谐叶盘振动模态特性，可供叶盘振动分析参考。

1 失谐多级叶盘振动局部化描述与评价

1.1 失谐叶盘的振动方程

叶盘结构的振动方程可表示为

式中：x为位移向量；M、C、K和f分别为系统的质量矩阵、阻尼矩阵、刚度矩阵和外力矩阵。

对于单级谐调叶盘结构来说，质量、阻尼和刚度矩阵具有循环周期对称性。当系统引入失谐时，系统的质量、阻尼和刚度矩阵的循环周期对称性就会被破坏，其矩阵均会发生变化，失谐系统方程可表示为

式中：M0、C0、K0分别为单级谐调叶盘结构的质量、阻尼和刚度矩阵；δM、δC、δK分别为其对应的失谐矩阵[1-2]。

对于多级谐调叶盘结构来说，由于通常级与级之间的叶片数不等，质量、阻尼和刚度矩阵的循环周期对称性会遭到破坏，级与级间周期对称性的不同称为“级间失谐”[1]，这种现象会影响响应的谐调性。但为了区分同级中引入非谐量的失谐叶盘，“级间失谐”多级叶盘仍称为谐调多级叶盘，而把由于盘片扇段引入失谐量的多级叶盘称为失谐多级叶盘。可见，当多级叶盘引入失谐时，式（1）～（4）仍然适用。

1.2 失谐多级叶盘结构振动模态局部化评价

迄今为止，在失谐周期结构和叶盘结构模态振型局部化的定量描述研究中有多种思路和方法，但主要是基于集中参数模型、连续参数模型和针对一般周期结构提出的模型[1-2]。

王建军、于长波等[1,6]在利用有限元法分析失谐叶盘振动模态时提出了几种评价模态局部化的局部化因子，并在典型失谐单级叶盘振动模态局部化评价中得到了较为成功地应用。

1.2.1 王建军、于长波提出的模态局部化因子[1,6]

首先定义第j个叶片无量纲化振型矢量。设uj为某阶模态振型矢量第j个叶片相应物理量的值（包括模态幅值、模态应力和模态应变能等）。这个相应物理量表示该阶模态第j个叶片相应物理量的值，为各叶片的相应物理量之和，从而可以定义第j个叶片相应物理量的无量纲值为

式中：Nb为该级叶盘结构的叶片数。

该无量纲振型元素实际上反映了相应的叶片振动能量在该阶模态振动能量中的比重。利用该无量纲的定义方法，分别定义了3种模态局部化因子，分别是振型局部化、应力局部化和应变能局部化因子。对于任一阶模态，若按式（5）求得的失谐前、后位移振型矢量的最大无量纲元素分别为ut和um，则可以定义失谐振动模态振型位移局部化因子为

如果将式（5）中模态位移分别换成模态应力和模态应变能，便是应力局部化因子和应变能局部化因子。位移和应力局部化因子均有一定的缺点。其中，位移局部化因子难以反映出复杂振动形式的失谐强弱规律；应力局部化因子受到叶片型面以及倒角的影响而可能存在应力集中。而应变能局部化因子很好地克服了上述缺点，但其运算上要花费更多的时间和更大的空间，不过，随着计算机运算能力的不断提高，这一缺点逐渐被弱化。

1.2.2 应用于多级失谐叶盘的模态局部化因子

从式（6）可知，如果将位移u换成振动应变能E，当Et=0/0（叶片不参与振动）或者结果很小，计算结果将失效或被放大较多，这对于多级叶盘的单级主导振动振型[3-5]的失谐识别阐述不够统一。因此，下面将采用类似于归一化的方法修改上述局部化因子。根据王建军、于长波提出的应变能局部化因子，本文提出了3种不同种类应变能局部化因子来判别失谐多级叶盘的失谐特性。

（1）失谐多级叶盘模态局部化因子

对于多级叶盘结构的某级叶片来说，任1阶模态，由式（5）求得失谐前、后叶片振动模态应变能的最大无量纲元素分别为Et和Em，做归一化改变后，则定义多级失谐振动模态应变能局部化因子为

规定：若 Et或 Em为0/0型数据，则 Et或 Em为 0（由定义，0≤Et和 Em≤1；实际上，Et、Em均大于 0；只有在理想状态下，Et、Em等于 0或 1）。

式（7）可进一步转化为

从式（8）可知，对失谐比较明显的阶次，相对来说识别的效果尚可；但经式（7）改进后，失谐的放大量减小，不利于弱失谐的识别。因此，提出1种适用于叶片小量失谐识别的多级叶盘高阶振动模态局部化因子。

（2）失谐多级叶盘高阶模态局部化因子

式（7）定义的多级叶盘模态局部化因子数值范围为[0,1]，而根据幂函数性质，利用开方的方法可实现对小量失谐的放大，而数值越接近1，放大量相对越小。该方法克服了式（7）对失谐相对较弱时识别不足的缺点；也可根据实际需要，对结果作开n次方处理，以使结果更易观察。

从物理意义上来说，在刚度不变的情况下，应变能与位移的平方成正比。因此，忽略刚度的小量变化时，将应变能局部化因子开平方后所得到的局部化因子可近似认为是对位移局部化因子的另1种诠释。

多级叶盘的某级叶片的高阶模态局部化因子可定义为

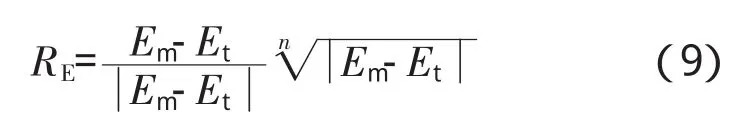
式中：Et、Em分别为由式（5）求得失谐前、后振动模态应变能的最大无量纲数值；为符号系数；n为放大阶次，可以根据需要来取。

通过简单算例检验式（9）。如果由式（7）计算的某级叶片的某2阶模态的第1阶次模态局部化因子分别为 0.01（弱失谐）和 0.9216（强失谐），则由式（9）计算的第2阶模态局部化因子分别为0.10和0.96。可见，对于弱失谐，采用高阶模态局部化因子识别效果更好。

（3）失谐多级叶盘3维模态局部化因子

由式（7）、（9）可知，上述定义只描述各阶最大失谐叶片的失谐程度，对总体失谐概况描述得不够具体。受3维振动谱线的启发，将式（7）进行改进，增加了叶片序号轴，于是，将2维局部化因子曲线改进成3维局部化因子谱线。

仍以应变能方法为例，对任意1阶模态来说，某级叶片失谐模态的3维局部化因子可描述为

式中：j为该级第j个叶片；E（j）m为失谐后该级第j个叶片振动模态应变能无量纲元素；Et为失谐前该阶振动模态应变能的最大无量纲元素。

2 改进的模态局部化因子在失谐多级叶盘模态分析中的应用

为了验证上述模态局部化因子的有效性，以典型2级叶盘模型（如图1所示）为例进行方法检验。

在图1示出的2级叶盘结构的有限元模型中，叶片失谐量通过改变叶片材料的弹性模量来实现，其中，2级叶片失谐标准差均为2%。2级叶片失谐模式分别如图2、3所示，各类叶片数量分别如图4、5所示，对应式（7）的 2级叶片前200阶局部化因子曲线如图6所示。由于式（7）目前已能够满足小量失谐识别要求，因此没有给出式（9）对应的高阶模态局部化因子曲线。对应式（10）的3维模态局部化因子曲线分别如图7、8所示，典型失谐2级叶盘模态振型和各叶片叶尖相对位移分别如图9、10所示。

从图6中可见，第1阶模态为2级节圆耦合振动模态，2级之间耦合强烈，不产生明显局部化现象；第2～54阶为第1级叶片1阶弯曲主导振动模态，由于为失谐级叶片主导振动，因此，第1级叶片局部化现象比较严重，同时也引起第2级叶片轻微失谐振动，但影响微弱，其中的典型振型和叶尖相对位移如图9所示；第55阶为第2级叶盘节圆耦合振动模态，2级均没有明显局部化现象；第56～98阶为第2级叶片1阶弯曲主导振动模态，由于为失谐级叶片主导振动，因此，第2级叶片局部化现象较为严重，同时也使第1级叶片产生轻微局部化振动；第99～102阶为2级耦合振动模态[5]，2级没有明显的局部化现象发生；第103～155阶为第1级叶片1阶扭转振动模态，该级有模态局部化现象，并能使第2级叶片也有轻微局部化振动；第156～16 2阶为耦合振动模态，既有单级叶盘耦合又包括2级耦合振动[5]，此时，第2级叶片局部化现象表现并不明显，其典型振型和叶尖相对位移图如图10所示；第16 3～200阶为第2级叶片1阶扭转振动模态，该级叶片有模态局部化现象，并能使第1级叶片也产生轻微局部化振动。这些现象在如图7、8所示的3维局部化因子谱线中均能明显反映出来。

综上所述，失谐多级叶盘振动局部化较易发生在失谐级叶片主导振动模态，失谐后会对相邻级叶片振动有微弱影响；在强耦合振动模态（包括单级叶盘耦合振动模态及多级叶盘耦合振动模态，如图6中绿色圆圈所示位置）[5]中，各级局部化现象均不严重。

3 结束语

本文主要研究失谐多级叶盘振动模态局部化的定量评价方法，定义了几种多级叶盘应变能局部化因子，并在失谐2级叶盘振动模态局部化分析中进行了检验。检验结果表明：这几种模态局部化因子能够较好识别失谐多级叶盘的失谐特性，识别结果与有限元法模态分析振型观察结果吻合得较好。

本文所述方法和结论可为叶盘结构振动分析提供参考和依据。参考文献：

[1]王建军，李其汉.航空发动机失谐叶盘振动减缩模型与应用[M].北京：国防工业出版社,2009：1-21.

[2]王红建.复杂耦合失谐叶片-轮盘系统振动局部化问题研究[D].西安：西北工业大学,2006.

[3]Bladh R, Castanier M P, Pierre C. Effects of multistage coupling and disk flexibility on mistuned bladed disk dynamics [J]. ASME Journal of Engineering for Gas Turbines and Power, 2003, 125（1）:121- 130.

[4]Song S H. Vibration analysis and system identification of mistuned multistage turbine engine rotors [D]. Ann Arbor：University of Michigan，2007.

[5]葛长闯，王建军，刘永泉.2级叶片-轮盘系统模态特性研究[J].航空发动机，2009，35（5）：19-23.

[6]于长波，王建军，李其汉.错频叶盘结构的概率模态局部化特性分析[J].航空动力学报，2009，24（9）：2040-2045.

Quantitative Assessment Method of Vibration Mode Characteristics for Mistuned Multistage Blisk

GE Chang-chuang1， WANG Jian-jun2， LIU Yong-quan1
（1.AVIC Shenyang Engine Design and Research Institute,Shenyang 110015,China;2.School of Jet Propulsion,Beihang University,Beijing 100191,China）

The quantitative assessment method of vibration mode characteristics for mistuned multistage blisk was studied.The vibration mode characteristics were evaluated by three kinds of localized factors based on the strain energy theory.The localized characteristics about the mistuned two-stage blisk were analyzed.The results show that three kinds of mode localization factors have well adaptability in evaluating the vibration of mistuned multistage blisk.

mistune;multistage blisk;mode;quantitative assessment;strain energy;localized factor

葛长闯（1979），男，工程师，主要从事航空发动机转子强度设计工作。