一维声子晶体中弹性波的全反射贯穿效应
刘启能
(1.重庆工商大学 废油资源化技术与装备教育部工程研究中心,重庆 400067;2.重庆工商大学 计算机科学与信息工程学院,重庆 400067)
声子晶体的概念是Kushwsha等人于1993年提出的。所谓声子晶体就是其密度和弹性常数呈周期性变化的人造带隙材料。弹性波在声子晶体中传播时会与声子晶体的周期结构发生相互作用,从而产生带隙。由于利用声子晶体的带隙可以十分方便地控制声波的传播,因此声子晶体在现代科学技术上有着十分广泛的应用前景。这使得对声子晶体的研究成为目前声学的前沿领域内一个活跃的问题。
目前对一维声子晶体的研究中,在研究方法、带隙特性、缺陷模特性以及滤波理论等方面都取得了丰富成果[1-11]。最近文献[12]中研究了电磁波在大于全反射角入射一维光子晶体时出现的渐逝波现象,得到了一些关于一维光子晶体中渐逝波的新特征。声子晶体与光子晶体有着相似的结构特征,那么弹性波在大于全反射角入射一维声子晶体时会出现什么新现象呢?这是一个值得研究的新问题。本文将对这一问题开展研究,即研究弹性波在大于全反射角入射一维声子晶体时出现的贯穿效应。
1 模型与理论
一维声子晶体是由有机玻璃(其密度为ρ1、厚度为d1)和水(其密度为ρ2、厚度为d2)两种介质周期性地交替构成。设入射空间和出射空间的介质也为水,即ρ2=ρ0。由于该声子晶体两边都为有机玻璃,因此它的周期数为N+0.5,N为整数。

图1 一维声子晶体Fig.1 1-D phononic crystal
为了研究弹性波在大于全反射角入射该一维声子晶体时出现的贯穿效应,利用本文作者在文献[13]中推出的固-流结构声子晶体的转移矩阵,则一个周期的转移矩阵m为:

其中:

矩阵中λ和μ为拉梅常数,θ为传播角,角标中L表示纵波、T表示横波。整个声子晶体的转移矩阵M为:
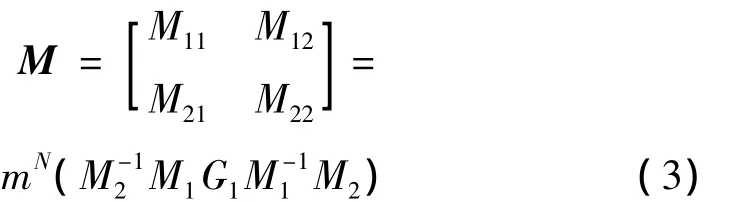
其中mN为前N个周期的转移矩阵为最后一层有机玻璃的转移矩阵。弹性波通过该声子晶体的反射系数r为:

不计材料的吸收时,弹性波通过该声子晶体的能流透射率T为:

利用(1)—(5)式可以研究弹性波在大于全反射角入射该一维声子晶体时出现的贯穿效应。下面的计算中,有机玻璃、水的密度、波速分别为:ρ1=1180kg/m3、ρ2= ρ0=1000kg/m3、v1L=2670 m/s、v1T=1120 m/s、v2L=v0L=1500 m/s,取 d1=v1L/(4f0)、d2=v2L/(4f0),f0为中心频率,取 f0=10000Hz。
2 贯穿效应
由波的折射定律可知,当波从波速小(ν0)的介质入射到波速大(ν1)的介质的分界面时会发生全反射现象,其全反射角为θm=arcsinν0/ν1。当弹性波从水中射入到该声子晶体时其全反射角为θm=0.6 rad。计算出弹性波从水中射入到有机玻璃单一界面上其透射率随入射角的响应曲线,如图1。由图1可以清楚地看出:当弹性波小于全反射角入射时透射率保持为T=0.88。当入射角接近全反射角时透射率迅速降低为0。当弹性波大于全反射角入射时透射率恒为0,弹性波不能进去有机玻璃内。即当弹性波大于全反射角入射时不能产生贯穿效应,并且这一特征与入射波的频率无关。
由(1)式—(5)式计算出频率为10000Hz的弹性波入射该声子晶体(N=5)时其透射率随入射角的响应曲线,如图2。由图2可以清楚地看出它与图1有明显的不同:其一,当弹性波小于于全反射角入射时,在入射角θ0=0-0.4 rad范围内出现了禁带,这是声子晶体的基本特性。其二,当弹性波大于全反射角入射时出现了新的现象,即在入射角 θ0=0.7 rad处和 θ0=1.1 rad处出现了两个明显的透射峰。我们将弹性波大于全反射角入射声子晶体时产生的透射现象称为全反射贯穿效应。为了研究贯穿效应的规律,下面分别从三个方面研究,即贯穿效应随入射角变化的特性、贯穿效应随介质厚度变化的特性、贯穿效应随周期数变化的特性。

图1 单一界面上透射率随入射角的响应曲线Fig.1 Response curves of transmissivity of interface versus incident angle
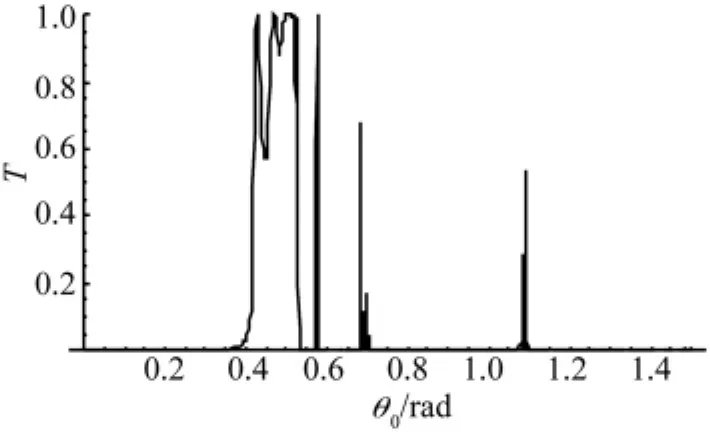
图2 声子晶体的透射率随入射角的响应曲线Fig.2 Response curves of transmissivity of phononic crystal versus incident angle
2.1 贯穿效应随入射角的变化
为了研究贯穿效应随入射角的变化规律,固定N=5,计算出透射率随入射角和频率的响应曲线,如图3。在图3中x轴表示入射角,y轴表示入射波频率,z轴表示透射率。由图3可以看出:
(1)在入射角大于全反射角θm=0.6 rad的区域内出现了两条明显的透射峰带,称它们为贯穿峰带。第一条出现在入射角θm=0.7 rad附近,第二条出现在入射角θ0=1.1 rad附近,并且第二条比第一条更加明显。
(2)两条贯穿峰带的频率都随入射角的增加而迅速减小。
(3)对于第一条贯穿峰带,当入射角从0.65 rad 变到0.72 rad 时,对应的入射波频率从11000Hz降低到9000Hz。对于第二条贯穿峰带,当入射角从1.05 rad 变到 1.14 rad时,对应的入射波频率从11000Hz降低到9000Hz。

图3 透射率随入射角和频率的响应曲线(N=5)Fig.3 Response curves of transmissivity versus incident angle and frequency(N=5)
(4)第一条贯穿峰带随入射角的增加而更加明显。第二条贯穿峰带随入射角的增加而减弱。
(5)两条贯穿峰带都不仅是一个单一峰带,而是多峰带的结构。
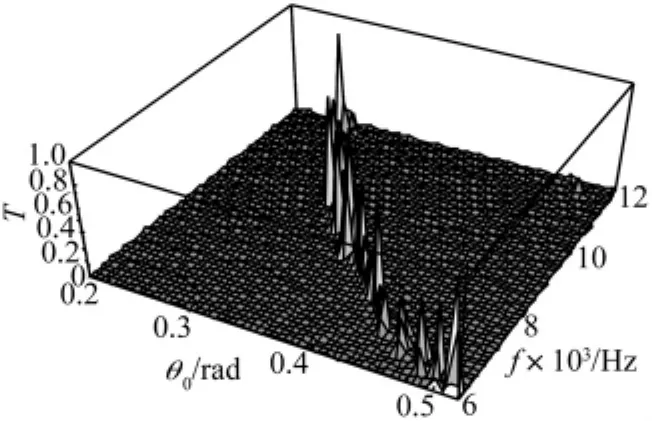
图4 透射率随厚度和频率的响应曲线(N=5)Fig.4 Response curves of transmissivity versus thickness and frequency(N=5)
2.2 贯穿效应随介质厚度的变化
介质厚度是指构成声子晶体的两层介质的厚度,即 d1和 d2。为了研究方便令 d1=XνL1/f0、d2=XνL2/f0,X为无量纲的参变量,当介质材料一定时(波速一定)介质厚度正比于X。因此可以用X描述介质的厚度,这里就通过X的变化来描述介质厚度的变化。固定N=5。
在入射角为θ0=1.0 rad处(第二条贯穿峰带上),计算出透射率随厚度和频率的响应曲线,如图4,由图4可以知:当入射角一定时,贯穿峰带的频率随介质厚度的增加而减小。当X=0.25时对应的频率为12000Hz,当X=0.52时对应的频率降低为6000Hz,并且是非线性变化。
2.3 贯穿效应随周期数的变化
为了研究周期数对贯穿效应的影响,固定d1=ν1L/(4f0)、d2=ν2L/(4f0),计算出N=3时透射率随入射角和频率的响应曲线的俯视图,如图5。比较N=3和N=5(图5和图3(b))两个不同周期的情况可以得出:
(1)周期数N=3和N=5两种情况下对应的两条贯穿峰带在图中的位置没有变化,这表明声子晶体的周期数对贯穿峰带的整体位置没有影响。
(2)周期数N=3的两条贯穿峰带内部结构比N=5的两条贯穿峰带内部结构要简单,这表明声子晶体的周期数对贯穿峰带的内部结构要产生影响。
下面研究周期数对贯穿峰带的内部结构的影响。计算出N=3、N=5、N=6三种情况下两条贯穿峰带随频率的响应曲线,如图6(a)、6(b)、6(c)(在第一条贯穿峰带上取入射角θ0=0.7 rad,在第二条贯穿峰带上取入射角 θ0=1.08 rad)。由图6(a)、6(b)、6(c)可以得出:
(1)同一周期的两条贯穿峰带的内部结构是相同的。如周期数N=5时其两条贯穿峰带都由5个透射峰构成,并且同一贯穿峰带内相邻两个透射峰的频率间隔近似相等。
(2)同一贯穿峰带内的透射峰数随周期数的增加而增加,并且两者的数目相等。

图5 透射率随入射角和频率的响应曲线(N=3俯视图)Fig.5 Response curves of transmissivity sus incident angle and frequency(N=3 top view)
为什么会在一维声子晶体中产生全反射贯穿效应呢?下面给予定性的解释。该一维声子晶体可以看成N个由两边为有机玻璃中间夹一层水的单元构成,如果入射角大于全反射角的弹性波进入该单元内,弹性波就会在水层中间往复地全反射,从而产生共振现象。因此每个这样的单元对于大于全反射角传播的弹性波就是一个谐振腔,弹性波在谐振腔内发生共振时,由量子理论可知弹性波就会在腔壁产生隧道贯穿效应。入射角大于全反射角的弹性波是怎样进入该一维声子晶体的第一层有机玻璃的呢?这可由渐逝波解释。入射角大于全反射角的弹性波并不是完全不能进入有机玻璃,而是以渐逝波的形式进入有机玻璃一定的深度。为了说明这一问题,计算出弹性波在大于全反射角(θ0=0.7 rad)进入有机玻璃时其透射率随有机玻璃厚度的响应曲线,如图7。在图7中横坐标d表示有机玻璃的厚度,以入射波的波长λ为单位。由图7可以看出,渐逝波可以进入有机玻璃的深度约为0.5个波长,而一维声子晶体中有机玻璃层的厚度只有四分之一波长。因此弹性波能够通过一维声子晶体的有机玻璃层后进入水层,并且在水层中引起了波的共振现象。从而在一维声子晶体中产生全反射贯穿效应。

一维声子晶体的全反射贯穿效应的透射峰与一般情况下一维声子晶体的两个带隙之间的透射峰既有区别又有联系。其主要区别在于两者产生的物理机理不同,全反射贯穿峰产生的物理机理是由于弹性波在一维声子晶体中发生的共振隧道贯穿效应,而两个带隙之间的透射峰产生的物理机理是由于弹性波在一维声子晶体中产生的能带效应。其二者的联系在于全反射贯穿峰的频率要受到能带频率范围的限制,即全反射贯穿峰的频率应在导带允许的频率范围内。
另外全反射贯穿效应与共振隧穿的也有区别和联系。全反射贯穿效应是特殊条件下产生的共振隧穿效应,即在全反射条件下、在渐逝波能够通过有机玻璃层的条件下产生的共振隧穿效应。因此,全反射贯穿峰的频率应满足共振条件。

图7 透射率随有机玻璃厚度的响应曲线Fig.7 Response curves of transmissivity versus thick
3 结论
前面利用转移矩阵法研究了弹性波在大于全反射角入射一维声子晶体时所产生的全反射贯穿效应。得出了贯穿效应随入射角的变化规律、贯穿效应随介质厚度的变化规律以及贯穿效应随周期数的变化规律。并利用波的量子理论和渐逝波的理论对一维声子晶体的全反射贯穿效应作出了定性的理论解释。
一维声子晶体中弹性波的全反射贯穿效应是一维声子晶体研究中的新现象,值得进一步研究。特别是从理论上对该现象进行定量的解释还有待深入研究,我们将继续对这一问题进行深入的研究。
[1]Jesen J S.Phononic band gaps and vibrations in one-and twodimensional mass-spring structures[J].Journal of Sound and Vibration,2003,266(5):1053-1078.
[2]Wang G,Yu D L,Wen J H.One-dimensional phononic crystals with locally resonant structures[J].Physics Letters A,2004,327(5-6):512-521.
[3]曹永军,董纯红,周培勤.一维准周期结构声子晶体透射性质的研究[J].物理学报,2006,55(12):6470-6473.
[4]温激鸿,王 刚,刘耀宗.基于集中质量法的一维声子晶体弹性波带隙计算[J].物理学报,2004,53(10):3384-3387.
[5]王文刚,刘正猷,赵德刚 .声波在一维声子晶体中共振隧穿的研究[J],物理学报,2006,55(9):4744-4747.
[6]曹永军,杨 旭.广义Fibonacci准周期结构声子晶体透射性质的研究[J]物理学报,2008,57(6):2620 -2624.
[7]郁殿龙,刘耀宗,王 刚.一维杆状结构声子晶体扭转振动带隙研究[J],振动与冲击,2006,25(1),104-107.
[8]刘启能.一维声子晶体的传输特性[J].人工晶体学报,2008,37(1):179 -182.
[9]刘启能.弹性波斜入射声子晶体的传输特性[J].应用力学学报,2009,26(2):397 -340.
[10]刘启能.固-固掺杂结构声子晶体中弹性波的缺陷模[J].计算力学学报,2010,27(1):151-156.
[11]曹永军,杨 旭,姜自磊.弹性波通过一维复合材料系统的透射性质[J].物理学报,2009,57(11):7735-7738.
[12]Fang Y T,Liang Z C.Unusual transmission through usual one-dimensional photonic crystal in the presence of evanescentwave [J]. Opt Commun, 2010,283:2102-2106.
[13]刘启能.固-流结构声子晶体中弹性波能带的色散研究[J].人工晶体学报,2009,38(1):107 -111.

