一种改进的基于相位差法的频谱校正方法
胡文彪,夏 立,向东阳,吴正国
(海军工程大学 电气与信息工程学院,武汉 430033)
频谱分析是数字信号处理的重要手段。由于FFT和谱分析只能在有限的时间区间内进行,不可避免地造成由于时域截断产生的能量泄露,使谱峰值变小、精度降低。已有研究表明,加矩形窗时单谐波频率成分的幅值误差最大可达36.4%[1],即使加其它窗时,也不能完全消除影响,如加Hanning窗时,只进行幅值恢复时最大误差仍高达15.3%,相位误差高达90°。因此采用各种有效的方法对频谱进行校正具有十分重要的意义。
目前国内外学者[1-21]在频谱校正方面做了大量研究工作,提出的频谱校正方法主要有:能量重心法[2,3]、比值法[4-6]、FFT+DFT 谱连续细化法[7]、相位差法[8-18]。其中采用相位差法进行校正时,幅值校正公式也完全依赖于窗函数的谱函数。在实际的工程应用中,窗函数的选择十分重要。根据不同的情况,选择适当的窗函数,可以取得比较好的效果。以密集频谱的情况为例,为确保校正精度,选取的窗函数的旁瓣必须能够快速衰减,避免不同频率分量的主瓣和旁瓣之间互相影响。Kaiser窗可定义一组可调的窗函数,其主瓣能量和旁瓣能量之间的比例近乎最大,且可自由选择主瓣宽度和旁瓣高度之间比重,本来十分适合密集频谱的情况。但由于Kaiser窗的窗函数十分复杂,其谱函数数学表达式无法求出[16],限制了Kaiser窗的应用。因此基于相位差法,研究一种通用的不依赖窗谱函数的具有统一的幅值校正公式的校正方法具有十分重要的意义。
1 相位差校正法
设有一周期信号x(t)=Acos(2πf0+t+θ),其傅里叶变换变换结果为:

式中:f=kfs/n=kΔf,Δf为频率分辨率。
对信号x(t)加长度为T(T=N/fs,fs为采样频率)的窗wT(t)。wT(t)是由对称窗w(t)右移T/2得到的。w(t)的窗谱函数为W(f),wT(t)的窗谱函数WT(f)相对于 y轴来说有一个相移因子 e-jπfT,即:

加窗后的信号x(t)wT(f)的傅里叶变换根据卷积定理可表示为:

对x(t)wT(f)做N点的FFT,由于频率分辨率Δf不可能无限小,不妨设f0=(K-ΔK)Δf,其中K为整数,ΔK∈[-0.5,0.5]为归一化的频率修正量。那么离散频谱的峰值应该出现在第K根谱线上,对应的相位为:
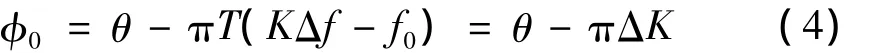
将窗函数wT(f)的中心再右移aT,这时产生的相移为e-j2πafT,同样做N点FFT后得到信号加窗后的相位为:

则两次计算所得的相位差为:

这里可以看出Δφ的取值在(-2π,2π)区间,而实际上相位是反正切函数,主值范围为(-π,π)。因此相位差Δφ需要做适当调整:

那么归一化的频率修正量为

假定频谱中出现峰值的第K根谱线的系数为X(K)=RK+jIK,则信号的幅值和相位的校正公式分别为:

从式(9)可以看出,幅值校正完全依赖于窗函数的谱函数W(f)。加不同的窗,窗谱函数W(f)不相同,幅值校正公式也各不相同。实际上即使是常用的窗函数,其谱函数也十分复杂,计算时只能做近似处理。甚至有些窗函数本身就比较复杂,其谱函数的解析表达式根本难以取得。这就极大地限制了不同应用场合窗函数选择的灵活性。因此研究一种不依赖窗谱函数的校正方法具有十分重要的意义。
2 改进算法
对于一个 N 点序列 x(n),n=0,1,…,N -1,其信号频率为f0,采样频率为fs,其离散傅里叶变换的逆变换表达式为:

每一个ek都是一个复正弦序列。若信号频率f0=代表的是一个频率为f的复正弦序列,那么0对应的坐标X(K)有很明确的物理意义,可以直接计算信号的幅值和相位。若信号频率,就会发生频谱泄漏。
将 e0,e1,…,eN-1同时乘以一个 N 点序列可以得到一组新的基。即:

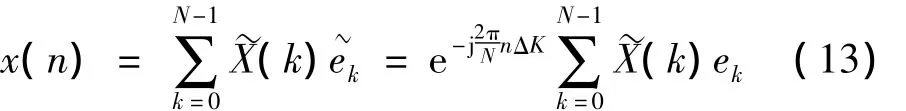

可以看出式(14)是一个标准的离散傅里叶变换逆变换的表达式。式中的系数(K)可以通过对N点序列(n)做DFT或FFT计算。这一点在物理意义上比较明确,即:序列x(n)的信号频率f0落在离散频谱上的两根谱线之间,因而会产生频谱泄漏;将x(n)乘以一个序列,相当于将信号做了一个频移,产生的新的序列的信号频率正好对准离散频谱上的第K根谱线,因此不会产生泄漏。考虑到加窗后频谱的幅值受窗函数影响降低,设加窗信号做DFT或FFT所得的第K个系数为:

则根据式(9)、式(10)和第2节的分析,原信号x(n)的幅值和相位校正公式为:

式中W(0)为w(n)的直流分量,不需要知道窗谱函数的表达式,只要对N点的窗取均值就可以求得。
因此本文的方法可归纳为:
第一步:采用相位差法求归一化的频率修正量ΔK。
3 仿真研究
用计算机生成信号:

采样频率1024Hz,作谱点数为1024,频率分辨率为1Hz。选用矩形窗,进行仿真研究。仿真结果如表1所示。

表1 加矩形窗的校正结果Tab.1 Correction results for rectangle window function
从表1中可以看出,在加矩形窗的条件下,各分量校正后频率、幅值、相位的精度有明显的提高。其中频率间隔较远的分量(52.8Hz和210.35Hz的分量)的频率最大误差为0.0025个频率分辨率,幅值最大误差为0.52%,相位最大误差为0.74°。频率间隔较近的分量(150.2Hz和154.25Hz的分量)校正精度相对降低,最大频率误差为0.0047个频率分辨率,幅值最大误差为1.47%,相位最大误差为1.52°。这主要是由于2个频率分量靠近时,不同分量的主瓣和旁瓣互相干涉造成的。通过加不同的窗函数,使旁瓣更快速地衰减,可以提高校正的精度。
这里为便于比较幅值校正精度,信号各分量的幅值都是1。而实际上2个频率靠近的分量由于幅值不同,互相之间影响造成的误差精度也各不一样。同时为比较频率靠近的分量互相之间的影响,将式(18)信号中的150.2Hz的分量的幅值提高到100,其他参数保持不变。分别加矩形窗、汉宁窗和凯泽窗,进行仿真研究。其中凯泽窗的形状参数β为10。仿真结果如表2所示。从表2可以看出:
(1)矩形窗的校正精度最差,由于有幅度为100的150.2Hz频率分量存在,其旁瓣对各幅值为1的分量都产生了较大的影响,误差很大,仅150.2Hz分量自身校正精度较高,频率误差为0.00017个频率分辨率,幅值误差为0.03%。
(2)加汉宁窗后,频率间隔较远的2个分量(52.8Hz和210.35Hz的分量)校正精度很高,频率最大误差为0.00001个频率分辨率,幅值最大误差为0.003%,相位最大误差为0.00372°。频率间隔较近的2个分量中,150.2Hz的分量的校正精度也高,幅值误差为0.0011%。可见 154.25的分量由于幅值较小,对150.2Hz分量的影响也较小。但154.25Hz的分量受150.2Hz分量的影响较大,幅值误差高达6.02%。
(3)加凯泽窗后,校正效果最好,各分量的校正精度都很高。其中154.25Hz的分量受临近的150.2Hz分量的影响较大,幅值误差在各分量中达到最大,也只有 1.07%。

表2 加不同窗函数的校正结果Tab.2 Correction results for different window functions
通过三种窗函数的比较,可以看出对于不同的工程背景和精度要求,选择合适的窗函数,可以达到令人满意的校正效果。
4 感应电机转子故障诊断实例
转子故障是感应电机的常见故障。转子发生故障时,感应电机的三相定子电流在基波电流分量的两侧会出现1±2s)f0的故障特征频率分量(其中f0为基波频率,s为转差率),这些特征频率分量的幅值与故障严重程度直接相关。正常工况下,感应电机的转差率较小,不超过6%。因此这些特征频率分量在频率上与基波电流分量靠得很近,属于密集分布的频谱。而且这些分量在幅值上与基波分量相比非常小,容易被基波分量的泄露淹没。现有的文献通常通过各种变换方法将基波电流分量转化为直流量,故障特征频率分量转化到低频段[22-26]。这样做能够避免基波分量泄漏的影响,对故障特征频率分量的提取比较有利,能够通过检测是否存在故障特征频率分量来判断是否出现故障,属于定性分析。但是故障特征频率分量自身同样会发生泄漏,如果不加以考虑,测得的故障特征频率分量的幅值仍然是不准确的,难以实现对故障严重程度的量化。采用改进的基于相位差法的频谱校正方法,可以不经过变换,直接对定子电流进行频谱分析,准确计算故障特征频率分量的幅值,实现对转子故障的定性和量化。

图1 A相电流波形图Fig.1 The waveform of A phase current

图2 A相电流的频谱图Fig.2 A phase current spectrum
实验电机采用的是Y132M-4型感应电机。一根转子断条的情况下,电机运行稳定后测得的定子A相电流波形和频谱分别如图1、图2所示。其中图2的频谱图是对数据长度为10 s的数据加矩形窗后用FFT算法计算得到的。感应电机由电网直接供电,基波频率f0接近50Hz。根据测得电机转速可计算出2sf0=2.2Hz。但从图2中可看出,基频分量两侧47.8Hz和52.2Hz的故障特征频率分量基本上已被基波分量的泄露淹没,很不明显,难以作为转子故障诊断的判据。
直观上看,图1中基波电流的幅值应该在15 A左右,但是图2频谱中50Hz的基波分量的幅值只有9.8787 A,可见泄露非常严重。取一段7.5 s长的数据,分别对前5 s和后5 s的数据加凯泽窗进行计算,采用相位差法求得频率校正量后,再用本文提出的方法对f0、(1±2s)f0的分量的幅值进行校正,取得了较好的效果。各分量的幅值如表3所示。

表3 基波与故障特征分量的校正结果Tab.3 Correction results of fundamental component and fault signature frequency components
5 结论
传统的相位差校正法在校正出频率校正量后,幅值校正依赖于窗函数的谱函数的解析表达式,造成采用不同的窗函数时校正公式各不一样。而一些复杂的窗函数,其谱函数根本难以求出。本文基于相位差校正法,在校正出频率校正量以后,对幅值校正进行改进,使之不再依赖窗函数的谱函数。这样就可以面对不同的工程应用背景和精度要求,自由地选择合适的窗函数,取得好的校正效果。仿真研究和应用实例表明,即使是频率密集分布的频谱,通过采用合适的窗函数,也可以达到较好的校正精度。
[1]丁 康,谢 明.离散频谱三点卷积幅值校正法的误差分析[J].振动工程学报,1996,9(1):92-98.
[2]丁 康,江利旗.离散频谱的能量重心校正法[J].振动工程学报,2001,14(3):354 -358.
[3]林慧斌,丁 康.离散频谱四点能量重心校正法及抗噪性能分析[J].振动工程学报,2009,22(6):659-664.
[4]丁 康,张晓飞.频谱校正理论的发展[J].振动工程学报,2000,13(1):14 -22.
[5]谢 明,丁 康.频谱分析的校正方法[J].振动工程学报,1994,7(2):172 -179.
[6]朱晓勇,丁 康.离散频谱校正法的综合比较[J].信号处理,2001,2001,17(1):91 -97.
[7]刘进明,应怀樵.FFT谱连续细化分析的傅里叶变换法[J].振动工程学报,1995,8(2):162 -166.
[8]刘 渝.正弦波频率快速估计方法[J].数据采集与处理,1998,13(1):7 -11.
[9]谢 明,张晓飞,丁 康.频谱分析中相位和频率校正的一种新方法——相位差校正法[J].振动工程学报,1999,12(4):454-459.
[10]丁 康,钟舜聪.通用的离散频谱相位差校正方法[J].电子学报,2003,31(1):142 -145.
[11]丁 康,朱小勇,谢 明,等.离散频谱综合相位差校正法[J].振动工程学报,2002,15(1):114-118.
[12]高云鹏,滕召胜,温 和,等.基于Kaiser窗相位差校正的电力系统谐波分析与应用[J].仪器仪表学报,2009,30(4):767-763.
[13]丁 康,杨志坚.改变窗长相位差校正法的改进与抗噪性能分析[J].华南理工大学学报,2007,35(10):210-213.
[14]丁 康,钟舜聪,朱小勇.离散频谱相位差校正方法研究[J].振动与冲击,2001,20(2):52-55.
[15]丁 康,朱小勇.适用于加各种窗的一种离散频谱相位差校正法[J].电子学报,2001,29(7):987-989.
[16]谢 明,张晓飞,丁 康.频谱分析中用于相位和频率校正的相位差校正法[J].振动工程学报,1999,12(4):454-459.
[17]汤宝平,陈建波,章国稳.基于相位差校正法的全息谱研究[J].振动与冲击,2009,28(8):99-102.
[18]黄云志,徐科军.基于相位差的频谱校正方法的研究[J].振动与冲击,2005,24(2):77 -80.
[19]张 强,张 频,张明童.加三角窗的频谱校正[J].振动与冲击,2009,28(2):96 -98.
[20]陈奎孚,王建立,张森文.短记录加汉宁窗的频谱校正[J].振动与冲击,2008,27(4):49 -51.
[21]段虎明,秦树人,李宁.离散频谱的频率抽取校正法[J].振动与冲击,2007,26(7):59 -62.
[22]Cruz S M A,Cardoso A J M.Rotor cage fault diagnosis in three-phase induction motors by extend Park's vector approach[J].Electric Machines and Power systems,2000,28(3):289-299.
[23]Cruz S M A,Cardoso A J M.Stator winding fault diagnosis in three-phase synchronous and asynchronous motors by the extended Park 's vector approach[J].IEEE Trans.On Industry Applications,2001,37(5):1227 -1233.
[24]Cruz S M A,Cardoso A J M,Toliyat H A.Diagnosis of stator,rotor and airgap eccentricity faults in three-phase induction motors based on the multiple reference frames theory[C].Conference Record of The 2003 IEEE Industry Applications Society Annual Meeting,Salt Lake City,USA,2003,П:1340-1346.
[25]刘振兴,尹项根,张 哲.基于Hilbert模量频谱分析的异步电动机转子故障在线监测与诊断方法[J].中国电机工程学报,2003,23(7):158-161.
[26]马宏忠,姚华阳,黎华敏.基于Hilbert模量频谱分析的异步电机转子断条故障研究[J].电机与控制学报,2009,13(3):371-376.

