强夯施工对塑性混凝土防渗墙的振动测试分析

陆凡东，方 向，董 文，丁 凯，李 栋

(解放军理工大学 工程兵工程学院，南京 210095)

强夯施工时，夯锤从高处自由落下对地基形成冲击和振动，除一部分转化为夯锤和土摩擦产生的热能外，其余大部分动能以纵波、横波和瑞利波的形式向外传播，其中瑞利波携带能量大、衰减慢，是构成强夯振动波对周边环境影响的主要原因。文献［1－2］认为瑞利波的有效穿透深度约为一个波长。文献［3］认为强夯振动引起的瑞利波波长在8 m～12 m之间，随着传播深度的增加，径向振动大幅衰减，对地基构筑物影响最大的是竖向振动。目前强夯振动波测试与控制的保护对象主要为地表及地表以上的构筑物，如民房、厂房、办公楼等［4－5］;文献［6］对减振沟的强夯降振效果进行数值模拟，并提出理论近似公式。

塑性混凝土防渗墙具有低强度、低弹性模量和大应变等特征，应力应变关系和破坏模式与土料相似，抗渗抗震效果良好［7］。目前，关于强夯施工对塑性混凝土防渗墙的振动测试研究在国内尚未见到报道。本文提出塑性防渗墙的强夯振动测试方案，并结合试验数据和希尔伯特黄变换(Hilbert-Huang Transform)方法给出振动测试成果。

1 工程概况

某核电站1－2号机组BOP区域分别由海域和海岸回填10 m～17 m和3 m～10 m而成，地基参数如表1所示。机组基坑负挖到地面10 m以下，为保持干施工的需要，主厂区内设有防渗墙，墙顶标高 +3.5 mPRD，场平标高+8.5 mPRD，主墙体平均高度21 m，墙厚0.8 m。在距防渗墙足够远的区域强夯能级初取8 000 kN·m，在保护范围内改用1 000 kN·m点夯，600 kN·m满夯，其中点夯两遍，满夯一遍，夯点呈等边三角形布置，夯点间距5 m。

表1 BOP区域地基分层参数Tab.1 Layered parameters of foundation in BOP area

在防渗墙附近进行试夯、正常强夯施工时，对防渗墙进行振动监测。通过试夯监测数据确定可行保护距离，确保防渗墙安全。

2 振动测试方案

2.1 监测仪器与控制标准

采用中国地震局工程力学研究所研制的G01通用数据采集仪和JBT型井下波速测试仪。防渗墙墙体各测点的质点振动(加)速度峰值不超过5 cm/s和0.1 g。

2.2 试夯振动监测

2.2.1 试验目的

(1)比较防渗墙不同深度的强夯振动数据，确定有效控制位置。

(2)比较速度和加速度控制标准。

(3)根据不同夯击能级确定防渗墙的有效保护范围，为正常强夯测振任务提供依据。

2.2.2 试验方法

(1)监测断面选择

在95 m长的防渗墙上选择墙体较深的两个监测断面:(a)A=6 768.452，B=3 171.848;(b)A=6 723.529，B=3 174.482。

(2)测点布置

由于在内径60 mm的测斜管内同时设置多个拾振器测试难度大、测试效果不佳，因此在第一个测斜孔两边0.5 m处各打一个铅直孔(孔径110 mm，孔深为8 m和12 m)。孔间距比夯检距小1～2个数量级，三孔可以近似为同一平面点坐标。获取振动规律后，在另一测斜孔位置旁打一个铅直孔，进行验证试验。

在第一个监测断面上选取某一标高同时测试速度和加速度，其他标高设置速度测点。如图1所示:以墙顶为±0 m标高，在－1 m标高设置1#加速度和2#速度测点，在－3 m、－5 m和－7 m标高设置3#、4#和5#速度测点;根据测试结果，以2 m升降步长调整测点位置。

图1 测点布置空间示意图Fig.1 Space distribution of monitor points

(3)夯点布置

初选夯击能级8 000 kN·m，夯检距50 m。夯检距由远至近;两遍点夯分别对待;当防渗墙测点的振动数据接近严格指标时，确定安全距离。图2为试验夯点布置图。

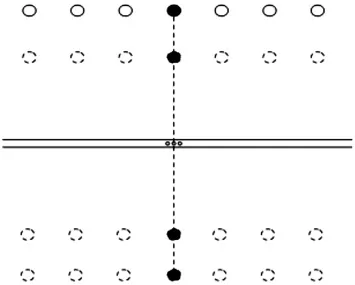
图2 试验夯点布置图Fig.2 Layout of test tamping points

(4)拾振器固定

胶囊充气后使三向拾振器与孔壁或孔底紧密接触，振动信号通过屏蔽电缆线接至地面信号采集分析仪，如图3所示。

2.3 正常强夯振动监测

采用无人值守模式:现场布置监测仪器和电脑主机，通过开机自动运行软件启动监测仪器，当监测数据超过预警值时，由无线收发硬件GPRS和手机卡向用户端报警。用户端同时接收现场设备的状态报告。

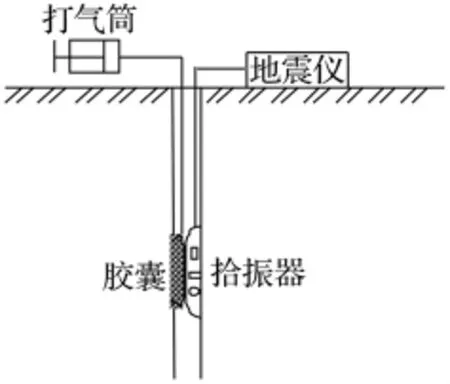
图3 拾振器固定示意图Fig.3 Fix of vibration pick-up

3 测试结果及分析

3.1 试夯结论

由表2可知:

(1)强夯施工引起塑性混凝土防渗墙的质点振动强度最大峰值集中在墙体上端，并随着测点标高的降低呈衰减趋势。

(2)加速度指标0.1 g比速度指标5 cm/s更严格。

表2 1#监测断面不同能级对应最大振动监测结果Tab.2 Vibration monitor results of 1#profile at different energy levels of dynamic co MPaction

(3)8 000 kN·m、3 000 kN·m、2 000 kN·m、1 500 kN·m、1 000 kN·m对应第一、二遍夯击的安全距离分别为 45 m、30 m、25 m、20 m、15 m 和 50 m、35 m、30 m、25 m、20 m。

3.2 不同夯击次数引起的振幅变化规律

图4(a)、图4(b)分别表示8 000 kN·m能级对应夯检距50 m以及1 000 kN·m能级对应夯检距20 m时，不同标高测点对应同一夯点不同夯击次数的振动强度峰值变化规律，前8次夯击属于第一遍点夯，后8次夯击属于第二遍点夯。随着夯击次数的增加，振动强度不断提高，回填土后，在第9次夯击时有所回落，继续夯击时振动强度逐渐增加，曲线趋于水平。

3.3 不同夯击能级的主频统计

强夯振动波由多种不同频率、相位和振幅的简谐振动叠加而成。主频指振幅最大的谐波分量对应的频率。表3列出不同夯击能级引起塑性混凝土防渗墙墙体振动的主频范围。

表3 不同夯击能级的主频统计Tab.3 Dominant frequency statistics under different damping energy

由表3可知:强夯施工不同能级引起塑性混凝土防渗墙的振动主频较低，均小于20 Hz;5个夯击能级的主频分布有差异，表现为小能级集中、大能级分散;加速度信号的主频分布比速度相对集中。

图4 不同夯击次数的振动强度变化规律Fig.4 Change law of vibration amplitude under different damping times

当强夯振动主振频率接近防渗墙的自振频率时，可能引起共振破坏。文献［7］给出塑性混凝土防渗墙墙土系统的初始自振频率在1.81 Hz～4.85 Hz之间，认为其抗压强度和极限应变随着围压的增加近似呈直线增大，导致自振频率随着应变变化呈下降趋势，除非地震强烈到使墙土系统各单元的动模量降到最低，否则不易发生共振。

3.4 同一夯击不同标高测点的能量分布

以规律性较好的振动速度为研究物理量，选取8 000 kN·m能级、夯检距50 m、第一遍第五次夯击作为研究对象，通过Hilbert－Huang Transform信号方法获得－1 m、－3 m、－5 m和－7 m标高测点速度信号对应三个振动方向的Hilbert能量谱和瞬时能量谱，如图5、图6所示，三列信号的振动方向由左向右依次为水平垂直于防渗墙墙体(V向)、竖直平行于防渗墙墙体(R向)和水平平行于防渗墙墙体(T向)。

由图5和图6可知:

(1)对于防渗墙墙体的振动输入能量，平行于墙体的方向显著高于垂直于墙体的方向。对于墙体振动的时间先后次序，V向和R向在－1 m标高率先振动，T向在－3 m标高测点和－1 m标高测点先后发生振动。说明强夯施工对该防渗墙的振动作用主要来自于地表浅层传播下来的瑞利波。

图5 不同测点各振动方向的Hilbert能量谱Fig.5 Hilbert energy spectrum of monitor points at different vibration directions

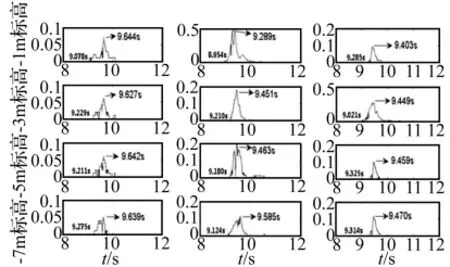
图6 不同测点各振动方向的瞬时能量谱Fig.6 Instantaneous energy spectrum of monitor points at different vibration directions

(2)在V向，各标高测点最大瞬时能量以及主频对应能量峰值相差不大。结合弹性力学理论可知，结构受到振动时产生的应力与振动速度呈正变关系。说明防渗墙墙体沿墙高的垂向应力分布比较均匀。

(3)在R向，－1 m标高测点对应6.7 Hz～12.4 Hz的频谱成分在－3 m标高大幅衰减，－5 m和－7 m标高测点的频谱成分分别在7.6 Hz和8.6 Hz处占主导。随着测点标高的降低，最大瞬时能量出现的时刻往后推迟，对应能量分别为0.47、0.18、0.21 和 0.11。

在T向，防渗墙墙体在－3 m标高测点率先振动，其次是－1 m、－7 m和－5 m标高。－3 m标高测点在频域7.6 Hz处含有较多频谱成分，对应最大瞬时能量也是各测点中最大的，为0.28，高于 －1 m标高的0.09、－5 m 标高的0.10 和 －7 m 标高的0.12。

－1 m和－3 m标高测点在土基第一层，－5 m标高测点在第二层和第三层的交界处，－7 m标高测点在第四层，比较发现:主频的降低导致相应能量峰值的增加。这是由于土基分层导致瑞利波发生频散效应，当主频降低时，瑞利波波速和波长增大所致。

4 结论

结合本工程场地土情况，分析得到以下四点结论:

(1)针对强夯施工的塑性混凝土防渗墙振动监测方案有效可行，为类似工程提供参照。试夯数据表明:加速度控制标准0.1 g比速度控制指标5 cm/s更严格，同时给出5个不同能级对应第一、二遍点夯的安全保护距离。

(2)强夯施工对塑性混凝土防渗墙的振动影响与防渗墙本身的埋深有很大关系。分析表明:塑性混凝土防渗墙墙体上端率先产生振动，并且振动强度最大。说明强夯振动对埋深仅为5 m的防渗墙而言，瑞利波的振动影响占主导地位。

(3)不同夯击能级引起塑性混凝土防渗墙墙体的振动主频小于20 Hz，且主频最小值比较靠近塑性混凝土防渗墙的自振频率。由于塑性混凝土防渗墙在外界振动荷载的作用下有良好的非线性协调能力，只要将振动强度控制在一定范围内，不易产生共振破坏。

(4)基于Hilbert-Huang Transform信号方法的时频域能量变化规律表明:塑性混凝土防渗墙墙体沿墙高的垂向应力分布比较均匀;由于分层介质对瑞利波传播特征的影响，当主频降低时，最大瞬时能量和主频对应能量小幅增加。

［1］牛志荣，路国运.土体受冲击时Rayleigh波作用机制探讨［J］.岩土力学，2009，30(6):1583 －1590.

［2］柴华友，吴慧明，张电吉，等.弹性介质中表面波理论及其在岩土过程中应用［M］.北京:科学出版社，2008.

［3］杨龙才，王炳龙.强夯施工对环境振动的影响分析［J］.华东交通大学学报，2007，24(2):16 －21.

［4］褚宏宪，史慧杰.强夯振动监测应用分析［J］.物探与化探，2005，29(1):88 －92.

［5］尹 坚，张良涛.地基强夯振动测试分析及防振动措施［J］.铁道工程学报，2009，127(4):17 －22.

［6］淳 庆，潘建伍.减振沟在强夯施工时的减振效果研究［J］.振动与冲击，2010，29(6):115 －120.

［7］王清友，孙万功，熊 欢.塑性混凝土防渗墙［M］.北京:中国水利水电出版社，2008.