变振幅激励下的液阻橡胶隔振器动态特性分析

潘孝勇，谢新星，上官文斌，

(1.宁波拓普集团股份有限公司，宁波 315800;2.华南理工大学 机械与汽车工程学院，广州 510640)

液阻橡胶隔振器动态特性定义为不同激励频率和振幅下，动刚度、滞后角变化特性［1］。在液阻橡胶隔振器动态特性的研究方面，目前主要以集总参数模型研究为主［1－6］。但集总参数模型参数的获取需要大量的实验，而部分集总参数模型参数必须先制作物理样件通过实验获得，也阻碍了其在产品设计工程中的应用，因此提供一种根据材料参数和分析模型直接预测液阻橡胶隔振器动态特性的方法尤为重要。

液－固耦合分析方法是一种有效的直接预测液阻橡胶隔振器动态特性的方法，但目前国内外已进行的关于液阻橡胶隔振器动态特性的液－固耦合分析研究，对其动态特性的振幅相关性和频率相关性考虑较少，故在较大程度上降低了动态特性预测的精度。

Karlsson和Persson研究了能同时描述振幅相关性和频率相关性的粘弹塑性模型［7］。结果表明，该模型能较好地表征纯橡胶零件的动态特性，但此模型并不能很好地体现液阻橡胶隔振器动态特性。Persson等人提出将粘弹性模型和弹塑性模型串联，以体现两者的相互耦合性，但并未得到验证。Svensson和Håkansson［8］提出了一个非线性弹簧模型、若干个流体模型和弹塑性模型并联的一维模型，在小振幅激励下该模型对液压衬套动态特性预测精度不够理想，因此其模型的振幅相关性方面有待改善。

本文基于网格叠加方法，将基于粘弹塑性的填充橡胶材料本构模型(Hyperelastic－Viscoelastic－Plastic，以下简称为VEP模型)应用于液阻橡胶隔振器的动态特性计算，并与基于粘弹性本构模型(Hyperelastic－Viscoelastic，以下简称为VE模型)的计算结果进行对比。结果表明，使用VEP模型时考虑了橡胶隔振器振幅相关性，其对橡胶隔振器动态特性的影响趋势与实验结果趋势相同。本文的方法和结果为液阻橡胶隔振器的动态特性进一步深入研究和前期开发提供了有效的分析工具。

1 液阻橡胶隔振器动态特性实验研究

以一典型液压衬套为例对其进行动态特性实验研究。液压衬套结构见图1。图2为该液压衬套在不同振幅和频率下的动态特性，由图可见，由于液压衬套阻尼结构的存在，液压衬套的动态特性具有频率和振幅相关性。即随着振幅的减小，液压衬套的滞后角峰值频率减小，且滞后角峰值增大;在高于峰值阻尼频率的频率范围内，液压衬套的动刚度随着振幅的增大而降低。

图1 一典型液压衬套结构示意图Fig.1 The structure sketch of a typical hydrobush

综合以上现象，可以得出:液阻橡胶隔振器不同于普通橡胶衬套，其动态特性的振幅相关性和频率相关性是相互耦合的。

2 基于VEP模型的网格叠加方法

通常有以下两类有限元计算方法用于橡胶隔振器动态特性计算分析，即基于结果叠加方法和基于网格叠加方法［3～4］。

基于结果叠加方法的原理［3］:建立N个(本实例N=4)有限元模型，包括一个包含超弹性－粘弹性材料模型的有限元模型和N－1个(本实例N－1=3)包含弹塑性材料模型的有限元模型。前者用于计算不同频率下的动态特性，后者用于计算不同振幅下的动态特性，然后将两者的计算结果进行频域叠加，即可获得橡胶隔振器在不同振幅和频率激励下的动态特性。

图2 实测的典型液压衬套的动态特性Fig.2 The measured dynamic properties of a typical hydrobush

网格叠加方法的基本原理［4］如图3所示，将目标网格模型复制N个(本实例N=3)，这些复制的模型保持独立的网格，但具有相同的节点及网格拓扑结构。将超弹性－粘弹性材料模型赋予一网格模型，而将各弹塑性材料模型逐一对应地赋予剩下的N个(本实例N=3)弹塑性网格模型。将四个带有材料属性的网格模型叠加，对叠加后的网格模型施加位移激励，一次性输出计算结果，通过拟合即可得橡胶隔振器在不同振幅和频率激励下的动态特性。

使用基于结果叠加方法进行计算得到的结果不能体现液阻橡胶隔振器中橡胶主簧动态特性的振幅相关性，而使用基于网格叠加方法则可体现此特性［4］。使用基于结果叠加方法一般须进行多次计算，占有较多的计算资源，误差也较基于网格叠加方法大。使用基于网格叠加方法，计算一次便能输出结果，较大程度的减少了计算量。基于上述优点，文中使用基于网格叠加方法开展液阻橡胶隔振器动态特性分析。

3 液压衬套液－固耦合有限元模型的建立

3.1 液压衬套有限元模型简化

考虑到图1的液压衬套物理结构较为复杂，建立有限元模型时需对其物理结构进行简化，如尼龙限位块、金属骨架与动态特性无关，可将其简化不予以考虑。如图4所示，根据液压衬套主簧的VEP特性、流道和液室的基本特征，建立液压衬套液－固耦合有限元模型。

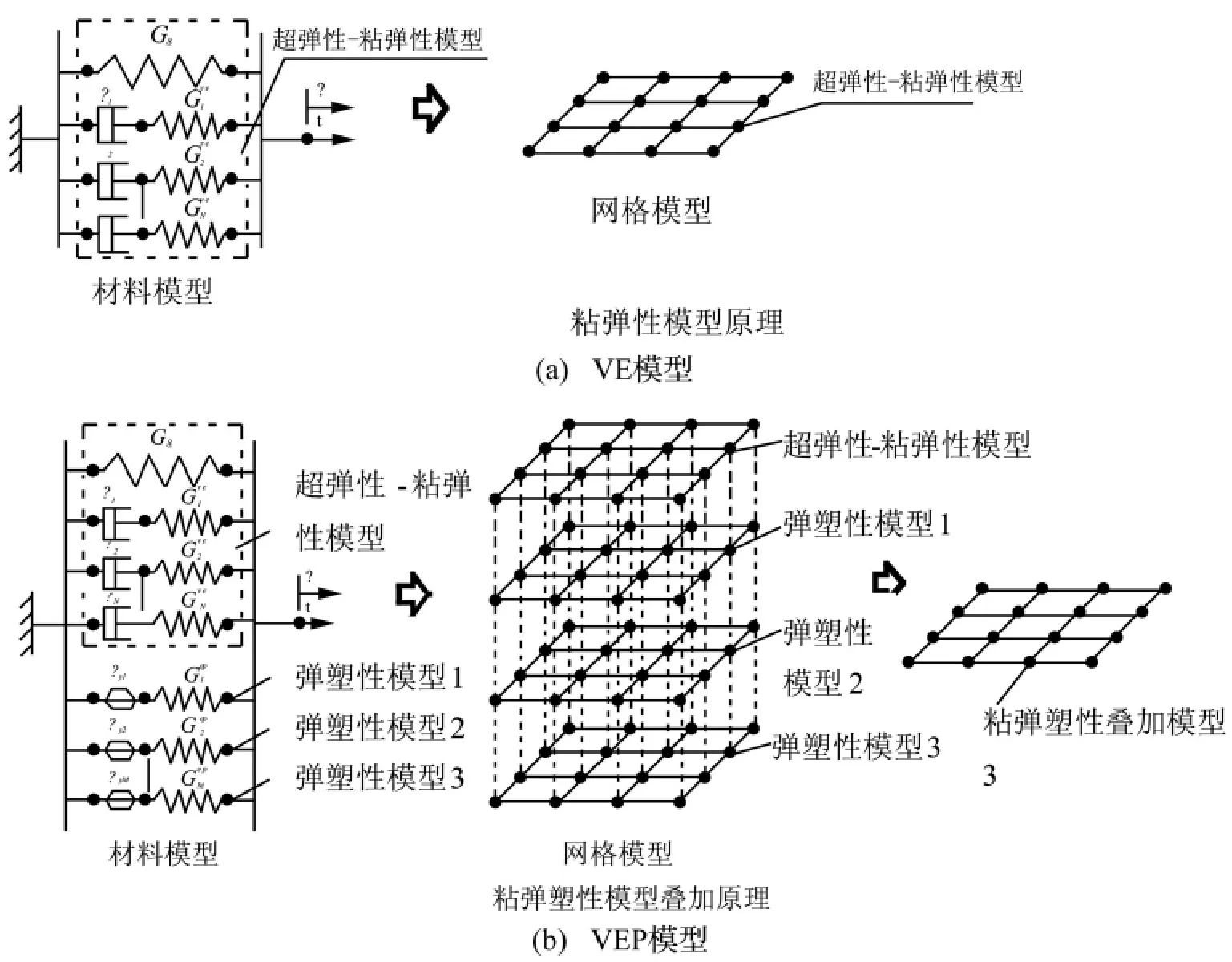
图3 VE模型和VEP模型的原理Fig.3 The principle of hyperelastic－viscoelastic(VE)model and hyperelastic－viscoelastic－plastic(VEP)model

图4 液压衬套液－固耦合有限元模型Fig.4 The fluid－structure interactive FE model of the hydrobush

在液压衬套液－固耦合有限元模型建立时，令与金属件硫化在一起的平面(图4(a)所指的加载面)上所有的节点与加载点刚性关联在一起;橡胶主簧的外表面(图4(a)所指约束面)与金属硫化在一起，并且该金属件固定安装在车身上，因此令该面上所有节点的位移为零;在橡胶主簧固体有限元模型中，橡胶主簧的凹陷表面(图4(a)颜色加深部分)与液体相接触的面(图4(b)流 －固耦合边界)定义为液 －固耦合面;如图4(b)所示，液体的有限元模型由径向布置的两个液室和两条惯性通道组成;图4(b)中的壁面与外管接触，形成液室，定义为刚性不可滑移的壁面;假定液体为不可压缩的，其密度(1.053 E－9ton/mm3)和粘度(5.8E －8MPa·s)可视为常数。

3.2 材料模型的建立

分别采用VE模型和VEP模型描述橡胶的材料属性，以期分析不同材料模型对液阻橡胶隔振器动态特性计算的影响。

在固体有限元模型中，橡胶材料选用超弹性本构关系中的Mooney－Rivlin模型描述液压衬套橡胶主簧的超弹性特性，Mooney－Rivlin 模型参数为:C10=0.2897，C01=0.0599。同时添加广义Maxwell模型描述液压衬套橡胶主簧的粘弹性特性。Maxwell粘弹性模型参数为:Gve1=0.111 MPa、Gve2=0.076 MPa、Gve3=0.194 MPa、Gve3=0.194 MPa、tr1=0.34 s、tr2=0.01 s、tr3=6 E －4 s。将网格模型复制成四个，将超弹性－粘弹性材料本构模型同时赋予其中一个网格模型;将三种弹塑性材料模型(Gep1=0.02 MPa、Ky1=0.1;Gep2=0.05 MPa、Ky2=0.027;Gep3=0.073 MPa、Ky3=0.005)逐一对应地赋予剩下的三个网格模型［4］。这些复制的模型保持独立的网格，但具有相同的节点及网格拓扑结构。将四个网格模型进行叠加，即得到具有超弹性－粘弹性－弹塑性(VEP)材料属性的网格模型。

4 液压衬套动态特性计算

4.1 液压衬套橡胶主簧动态特性计算对比

首先在不考虑液体作用的情况对固体有限元模型进行分析，将固体有限元模型的流－固耦合边界去除，其它条件与流－固耦合模型中的固体有限元模型条件相同。图5为该液压衬套在不同振幅和频率下的动态特性。由图5可知，当使用VE模型时，液压衬套主簧的动态特性并不随着振幅的变化而改变。而使用VEP模型时，液压衬套主簧的动刚度随着振幅的增加而降低，当振幅增到一定程度时，其动刚度基本上与VE模型相近;液压衬套主簧的滞后角随着振幅的增加而增加，当振幅很小时，其滞后角基本上与使用VE模型时接近。因此使用VEP模型进行液压衬套动态特性的流－固耦合计算，有助于准确表达橡胶主簧在不同振幅下对液压衬套动态特性的贡献。

图5 使用VE模型和VEP模型计算的橡胶主簧动态特性Fig.5 The dynamic properties of main rubber element of the hydrobush calculated by VE model and VEP model

4.2 使用VE模型液压衬套动态特性计算

对VE模型材料属性的固体模型及液体模型进行流－固耦合分析。当作用于图4(a)的加载点如图6的位移激励(频率=50Hz，振幅=0.2mm)时，可计算得到加载点的支反力见图6、液压衬套两对称液室压力见图7及液压衬套流道截面速度见图8。

图6 在位移激励下液压衬套支反力(VE模型)Fig.6 The reaction of the hydrobush with the displacement excitation calculated by VE model

由图6可见，在正弦位移激励下，加载点的反力滞后于激励位移，滞后角接近90°。由图7可见，两个径向液室的液体压力在位移激励下，其中一液室的压力变化提前于位移激励而另一液室的压力变化滞后于位移激励，滞后角和提前角也接近90°。而图8显示位移激励与流道截面速度近似反相位，这是由于位移向其中一侧加载时该侧压力的增大，液体向另一侧流动，导致流道截面速度与加载点位移方向相反。

图7 在位移激励下液压衬套液室压力(VE模型)Fig.7 The pressure of the hydrobush liquid chamber with the displacement excitation calculated by VE model

图8 在位移激励下衬套流道截面速度(VE模型)Fig.8 The flow velocity of flow passage cross－section of drobush with the displacement excitation calculated by VE model

图9 液压衬套的动态特性(VE模型)Fig.9 The dynamic properties of hydrobush calculated by VE model

图9为在不同振幅下液压衬套随频率变化的动刚度和滞后角曲线。由图可见，当使用VE模型进行流－固耦合有限元计算时，得到的液压衬套的动刚度和滞后角具有明显的频变特性和幅变特性，但在不同振幅下，阻尼峰值频率基本上不变，液压衬套动态特性的振幅相关性和频率相关性耦合不明显。液压衬套的滞后角峰值在60Hz左右出现，此现象主要是液压衬套惯性通道中的液体在该频率点共振所致。

4.3 使用VEP模型液压衬套动态特性计算

对VEP模型材料属性的固体模型及液体模型进行流－固耦合分析，加载条件与使用VE模型时相同。可计算得到加载点的支反力见图10、液压衬套两对称液室压力见图11和液压衬套流道截面速度见图12。由图10和图11可见，支反力，压力，截面速度三者表现出的特征趋势与使用VE模型计算时基本一致。

图10 在位移激励下液压衬套支反力(VEP模型)Fig.10 The reaction of the hydrobush with displacement excitation calculated by VEP model

图11 在位移激励下液压衬套液室压力(VEP模型)Fig.11 The pressure of the hydrobush liquid chamber with displacement excitation calculated by VEP model

图13为液压衬套在不同振幅下随频率变化的动刚度和滞后角曲线。由图可见，当使用VEP模型作为橡胶的材料模型进行液压衬套动态特性的计算时，得到的液压衬套动刚度和滞后角同样具有明显的频变特性和幅变特性。较之于使用VE模型区别在于液压衬套在不同振幅时的滞后角峰值频率不再相同，而是随着振幅的减小而后移，其峰值随着振幅的减小而升高。将两类模型计算结果与图2中一典型液压衬套的实测特性比较可知，VEP模型计算结果与实测动态特性趋势较为一致。

图12 在位移激励下衬套流道截面速度(VEP模型)Fig.12 The flow velocity of flow passage cross－section of hydrobush with displacement excitation calculated by VEP model

图13 液压衬套的动态特性(VEP模型)Fig.13 The dynamic properties of hydrobush calculated by VEP model

4.4 两类模型计算的液压衬套动态特性比较

图14～图15为比较不同激励振幅下，使用VE模型与VEP模型进行流－固耦合动态特性计算得到的液压衬套随频率变化的动态特性。

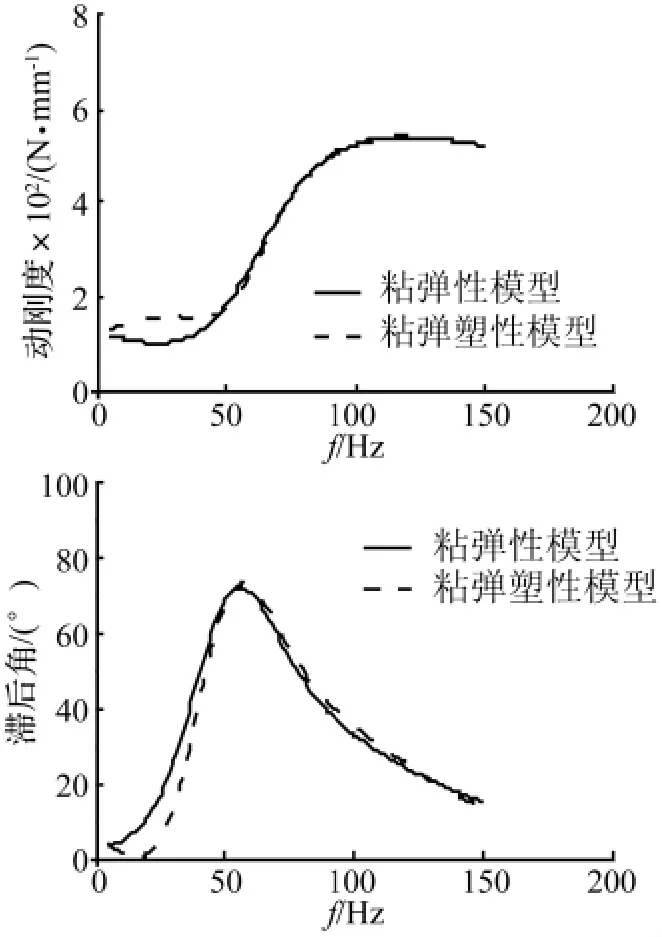
图14 振幅为0.2mm时液压衬套动态特性Fig.14 The dynamic properties of hydrobush at the amplitude of 0.2mm

图15 振幅为0.05mm时液压衬套动态特性Fig.15 The dynamic properties of hydrobush at the amplitude of 0.05mm

由图14可见，当液压衬套受较大的振幅(0.2mm)激励时，使用两种模型计算的液压衬套动态特性较为接近，其动刚度和滞后角曲线吻合较好;由图15可见，当振幅较小(0.05mm)时，使用VEP模型计算的液压衬套动刚度在高频段明显偏高，而其滞后角较之于VE模型时有一定程度的减小且其滞后角峰值频率后移，主要原因是受VEP模型计算的橡胶主簧动态特性振幅相关性影响导致，此现象符合典型液阻橡胶隔振器的滞后角特征。

5 结论

(1)基于网格叠加方法，建立了超弹性－粘弹性－弹塑性叠加的橡胶隔振器VEP模型，该方法较之于基于结果频域叠加方法应用更为简便;

(2)使用橡胶材料的网格叠加方法，对VE模型和VEP模型计算得到的液压衬套橡胶主簧的动态特性进行了对比，结果显示，VEP模型计算的液压衬套橡胶主簧的动态特性具有明显的幅变特性;

(3)经液压衬套的流－固耦合分析，VEP模型较之于VE模型更能表现液压衬套的频率相关性和振幅相关性的耦合特征。

文中的研究方法和成果可应用于液阻橡胶隔振器的前期开发设计。

［1］上官文斌.液阻型橡胶隔振器液－固耦合动力学特性仿真技术研究［D］.北京:清华大学，2003.

［2］潘孝勇，上官文斌，柴国钟，等.基于超弹性、分数导数和摩擦模型的碳黑填充橡胶隔振器动态建模［J］.振动与冲击，2007，26(10):6 －10.

［3］潘孝勇，上官文斌，柴国钟，等.橡胶隔振器动态特性计算方法的研究［J］.振动工程学报，2009，22(4):345－351.

［4］潘孝勇.橡胶隔振器动态特性计算与建模方法的研究［D］.杭州:浙江工业大学，2009.

［5］Berg M.A model for rubber springs in the dynamic analysis of railvehicle ［J］.Proceeding ofthe Institution of Mechanical Engineers，Part F:Journal of Rail and Rapid Transit，1997，211:95 －108.

［6］Berg M.A non－linear rubber spring model for rail vehicle dynamics analysis ［J］.Vehicle System Dynamics，1998，30:197－212.

［7］Svensson M， Håkansson M. Hydrobushing modelfor multibody simulations ［D］. Master's Thesis， Lund University，Sweden，2004.

［8］Karlsson F，Persson A.Modelling non－linear dynamics of rubber bushings－Parameter Identification and Validation ［D］.Master's Dissertation，Lund University，Sweden，2003.

［9］Nomura T，Hughes T J R.An arbitrary Langangian－Eulerian finite element method for interaction of fluid and a rigid body［J］. ComputerMethodsin Applied Mechanicsand Engineering，1992，95:115－138.

［10］Nomura T.ALE finite element computations of fluid－structure interaction problems［J］.Computer Methods in Applied Mechanics and Engineering，1994，112:291－308.