高速公路车辆行驶安全度评价模型研究

赵 圆，姚红云，闫冬梅，龙东华

（重庆交通大学交通运输学院，重庆 400074）

高速公路车辆行驶安全度评价模型研究

赵 圆，姚红云，闫冬梅，龙东华

（重庆交通大学交通运输学院，重庆 400074）

基于运动状态建立了高速公路车辆行驶安全度评分模型，可更加有效地实施实时交通预警。引进了一种新的速度离散度作为运动状态指标，分析了新定义的速度离散度与传统速度离散度-车速标准差之间的关系，表明两者有函数关系。在把新定义的速度离散度作为运动状态的基础上，加入了人、车、路、气候等因素，构成了驾驶员、车辆、车路、道路线形、气候、车辆行驶状态等6大指标，并筛选了各大指标下的子指标，建立了相应的评价指标体系。利用层次分析法计算各参数权重来构建模型，建立了总的车辆行驶安全度评分模型。实例验证表明:模型符合客观实际，具有一定的可行性。

高速公路;速度离散度;层次分析法;安全评分模型

高速公路是指能适应年平均昼夜小客车交通量为25 000辆以上、专供汽车分道高速行驶、并全部控制出入的公路［1］，其建设情况反映了一个国家和地区的交通发达程度，乃至经济发展的整体水平。高速公路在带来方便、快捷、高效的同时，也带来了大量的人员伤亡和财产损失，在道路交通安全事故中，高速公路百公里事故发生率是普通公路的4倍左右，且重大恶性交通事故时有发生。高速公路平纵线形设计的不合理，如平面曲线半径过小、纵线坡度过大，可能引起交通事故;驾驶员生理心理的不良状态，也可能引起交通事故;尤其是道路中车辆的超速行驶，引起追尾碰撞，都会造成安全事故。由于影响高速公路行车安全的因素复杂多样，有外部因素，也存在内部因素，所以，有必要建立一个有效的高速公路行车安全评价方法。笔者通过对高速公路的车辆行驶安全度的评价，来评估道路安全性，以期减少道路事故发生的概率。

道路车辆行驶安全度评价的方法有很多，有概率数理统计法（如事故绝对数法和事故率法）、强度分析法等，它们都是对交通事故的一种事后评价。如今事后评价已不能满足对交通安全的要求，综合评价方法（如层次分析法、基于模糊数学的评价法［2］、基于灰色聚类理论与人工神经网络技术的评价法［3］等），以及基于交通冲突技术的道路安全评价［4］，可以进行事前评价，能达到交通预警的目的。国外学者［5-6］对交通安全的评价比较多，但大多也集中于以上几种，这些评价方法只对静态指标进行综合评估，而忽略了实时车辆动态运动这个指标。无论道路参数是什么，车辆相关参数怎样，如果车辆停止运动，就不会发生交通事故，所以车辆运动状态这个指标是不可或缺的。为此，笔者引入车辆运动状态这个指标，此指标用速度离散度来衡量。

1 速度离散度与交通事故的函数关系

1964 年，D.Solomon［7］研究了速度离散度与交通事故率的关系，认为速度离散度是引起交通事故的原因之一，得出模型如式（1）:

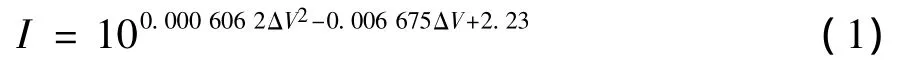
式中:I为10万车公里事故率，次/（106veh·km）;ΔV为车速与平均车速之差，km/h。

同济大学的杜博英［8］提出了事故率模型，力图将运行车速与速度梯度综合考虑，更加逼近客观事实。模型中的事故率不但包括已经发生的交通事故，而且对整条道路一定时间内的交通事故进行逻辑预测，这与以往的速度模型有着根本的区别。通过已有数据的分析与模型的预测，可以找出个别事故的严重路段，从而改善该路段的路况，将交通事故率控制在最低水平。

式中:I*为事故率，次/（106veh·km）;a为弹性系数，通过回归统计解出;V为运行车速，km/h;P为控制参数。

2 速度离散度的定义

为了研究交通流车速离散型的特征及分布规律，首先要给出车速离散度的定义，目前为止，对车速离散度的定义尚没有一个统一的定义。以往的一些研究中往往用标准差定义车速离散度，由于车速标准差与密度速度以及交通率具有一定的关系，并且具有统计学的意义，因此得到广泛的应用。标准差定义的车速离散度为:

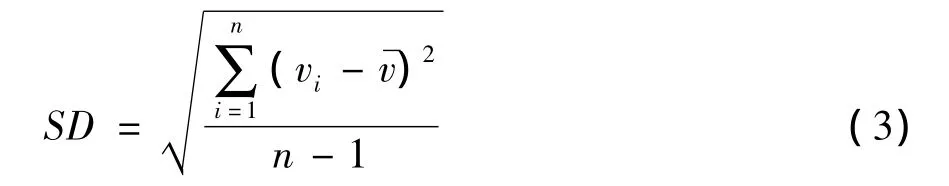
式中:vi为车辆经过断面观测点的地点速度为统计时间间隔内所有通过断面观测点的地点车速的算术平均值，;n为统计时间间隔内通过断面观测点的车辆数。

王昊［9］基于车辆的跟弛理论提出了一种新的速度离散度的定义方法，将统计间隔内所有通过观测点的n辆车相邻两车的地点速度之差的平均值作为速度离散度:

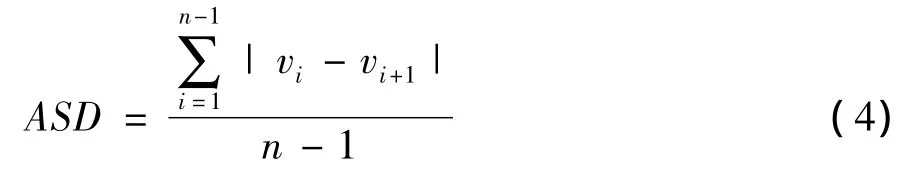
笔者选定一个车辆作为研究对象车辆，对象车辆与周围空间车辆发生交通关系。

高速公路上，研究的对象车辆车速越大，此车超车的机会也就越多，被后方车辆超车的机会越少;对象车辆车速越小，超越前方车辆的机会也就越少，但被后方车辆超越的机会也就越多。所以车辆发生事故的可能性包括车辆超车引起事故的可能性与车辆被超车所引起的事故的可能性，尽量减少车辆与前后方车辆的速度的离散，就可降低发生事故的可能。

以行驶于高速公路上某辆车作为研究的对象车辆，在某个时刻t，它经过高速公路断面i，在此断面i前方（行车方向）距离断面i长度为L及在此断面i后方（行车相反方向）距离断面i长度为L的两个断面作为界线，这两个界线与断面i之间存在两个路段，分别为路段R1、路段R2，如图1。

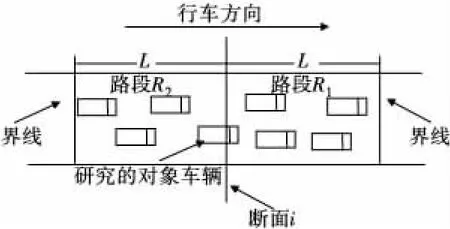
图1 速度离散度定义示意Fig.1 Speed dispersion diagram

速度离散度YSD定义为:

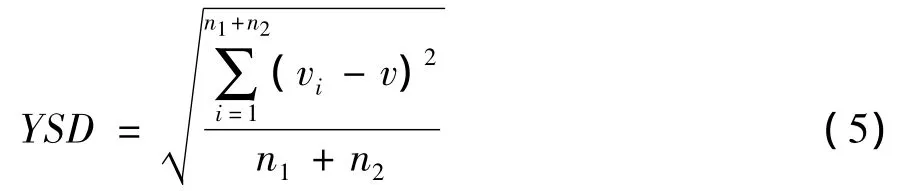
式中:vi为时刻t路段R1与R2内所有车辆的瞬间车速;v为时刻t对象车辆经过断面i的地点车速;n1、n2分别为路段R1与R2内的车辆数。

由于在车辆行驶的一小段距离上，车速基本不变，故路段R1内所有车辆曾经经过断面i时的地点车速可以代替时刻t路段R1内的各车辆瞬间速度，路段R2内所有车辆将要经过断面i时的地点车速代替时刻t路段R2内所有车辆的瞬间车速。速度离散度ZSD定义为:

式中:vi为路段R1内所有车辆曾经经过断面i时的地点车速及路段R2内所有车辆将要经过断面i时的地点车速;v为时刻t对象车辆经过断面i的地点车速;n1、n2分别为路段 R1与 R2内的车辆数。

所以有YSD≈ZSD，可用ZSD代替YSD。

新定义的速度离散度能反映出对象车辆与前后方车辆车速的离散程度。由于高速公路路段可分为无穷个断面，车辆行驶过程中经过这些断面，则在每个时刻的每个断面，车辆都将有一个速度离散度，作为此车辆运行状态的指标参数，所以速度离散度YSD是一个随时间变化的动态过程。车辆事故的发生可能是路段的任何一个断面，所以速度离散度将显得有意义。

3 两类描述方式之间的关系

标准差定义的车速离散度为:

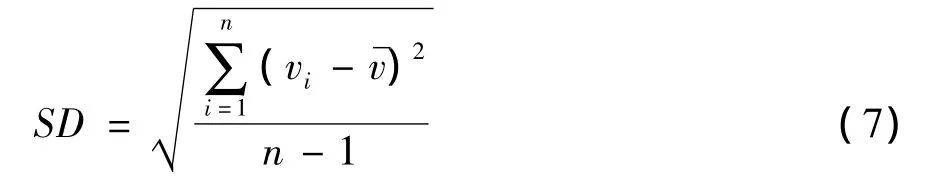
式中:vi为车辆经过断面观测点的地点速度;为统计时间间隔内所有通过断面观测点的地点车速的算术平均值，;n为统计时间间隔内通过断面观测点的车辆数。

由于高速公路上的交通流一般处于自由流状态，处于拥挤状态的可能性很小。笔者着重研究自由流状态下的情况。

早期的研究表明，自由流状态下地点车速通常服从正态分布，不妨假设地点车速样本服从正态分布，v～（μ，σ2），标准差定义的车速离散度的期望值为:

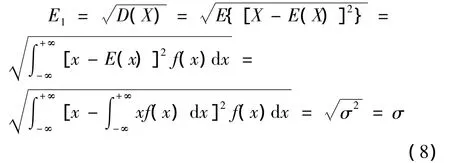
由于速度的非负性以及高速公路管理规定对于最高车速与最低车速的规定，这里x1≤x≤x2，所以准确形式期望值为:

式中:f（x）为随机变量x的概率密度函数，即正态分布概率密度函数，

文中定义的速度离散度为:

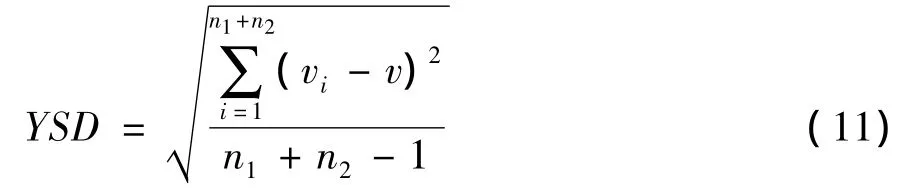
由于 ZSD几乎与 YSD相等，故用 ZSD代替YSD。其期望值E3为:

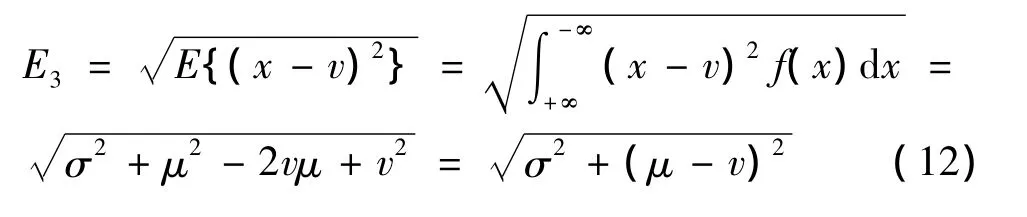
式中:v为时刻t对象车辆的地点速度。

由于速度的非负性以及高速公路管理规定对于最高车速与最低车速的规定，x1≤x≤x2，所以准确形式期望值为:

式中:f（x）为随机变量x的概率密度函数，即正态分布概率密度函数，

4 速度离散度与安全水平、事故率的关系

根据我国部分高速公路平均车速，车速标准离差与事故的统计数据，对平均车速车速标准离差和亿车公里事故率进行了回归分析［10］，得到

式中:AR为亿车公里事故率，次/（109veh·km）;SD为标准差定义的车速离散度。

美国联邦公路署研究报告（FHWA-RD-99-174）中给出了不同安全水平对应的事故率，如表1。

表1 不同安全水平对应的故事率Table 1 Story rates corresponding to different security levels

根据 AR=9.583 9e0.0553SD，可计算得到对应不同设计安全水平的车速标准离差，如表2。

表2 不同设计安全水平的车速标准离差Table 2 Speed standard deviation corresponding to different security levels

由YSD2=SD2+（μ-v）2计算得到对应不同安全水平本文所定义的车速离散度，见表3。

表3 对应不同安全水平的本文所定义的车速离散度Table 3 Speed dispersion defined in the paper corresponding to different security levels

5 评价模型的建立

5.1 基于AHP法的权重值计算

一级指标之间相互独立，且一级指标对应的二级指标之间也相互独立，各评价指标模型用多元线性方程来建立，采用层次分析法［11］来建立高速公路车辆行驶安全度模型。高速公路行车安全度评分模型的递阶层次结构:目标层A，一级指标层B，二级指标层，见表4。

表4 行车安全度评分模型的递阶层次结构Table 4 Hierarchical structure of traffic safety score model

根据多位评审专家所填写咨询表的统计分析，构造一级指标层B相对于总目标A的判断矩阵（表5）。

表5 一级指标层B相对于总目标A的判断矩阵Table 5 Comparison matrix of first indicator layer B relative to the overall goal A

表5矩阵具有满意的一致性，不需要进行调整。用MATLAB计算得到一级指标的权重系数为:0.386 5，0.157 3，0.099 1，0.063 1，0.039 6，0.254 2。

同理，构造判断矩阵（表6），计算二级指标相对于一级指标B1的权重值。

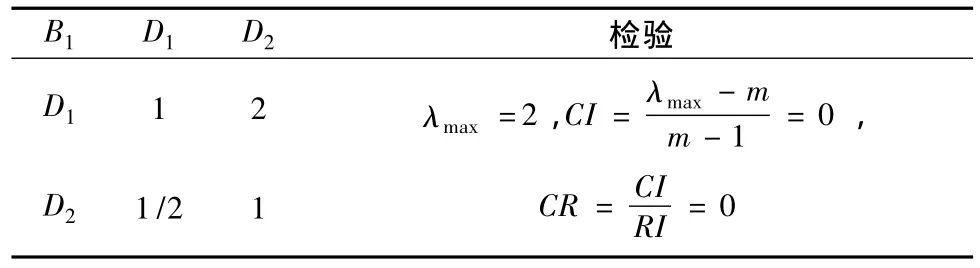
表6 二级指标相对于一级指标B1的判断矩阵Table 6 Comparison matrix of second indicator layer relative to first indicator layer B1

表6矩阵具有满意的一致性，不需要进行调整。计算得到一级指标B1对应的二级指标D1、D2权重值为:0.663 7，0.333 3。

构造判断矩阵（表7），计算二级指标相对于一级指标B2的权重值。

表7 二级指标相对于一级指标B2的判断矩阵Table 7 Comparison matrix of second indicator layer relative to first indicator layer B2

表7矩阵具有满意的一致性，不需要进行调整。计算得到一级指标B2对应的二级指标E1、E2、E3、E4权重值为:0.458 5，0.304 8，0.093 4，0.143 2。

构造判断矩阵（表8），计算二级指标相对于一级指标B3的权重值。

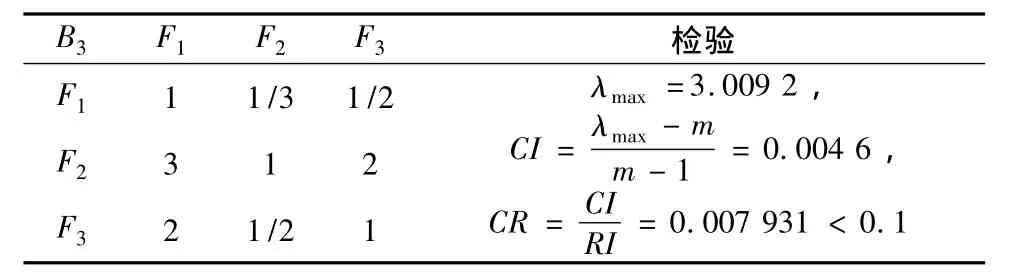
表8 二级指标相对于一级指标B3的判断矩阵Table 8 Comparison matrix of second indicator layer relative to first indicator layer B3

表8矩阵具有满意的一致性，不需要进行调整。计算得到一级指标B3对应的二级指标F1、F2、F3权重值为:0.163 4，0.539 6，0.296 9。

构造判断矩阵（表9），计算二级指标相对于一级指标B4的权重值。

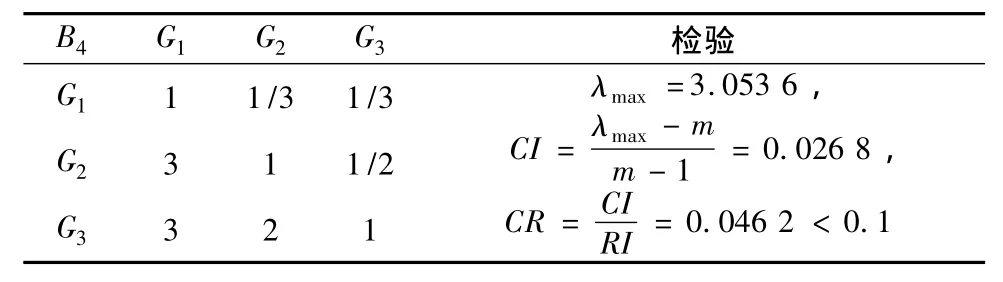
表9 二级指标对一级指标B4的判断矩Table 9 Comparison matrix of second indicator layer relative to first indicator layer B4

表9矩阵具有满意的一致性，不需要进行调整。计算得到一级指标B4对应的二级指标G1、G2、G3权重值为:0.139 6，0.332 5，0.527 8。

基于以上对权重值的计算，建立层次总排序，如表10。

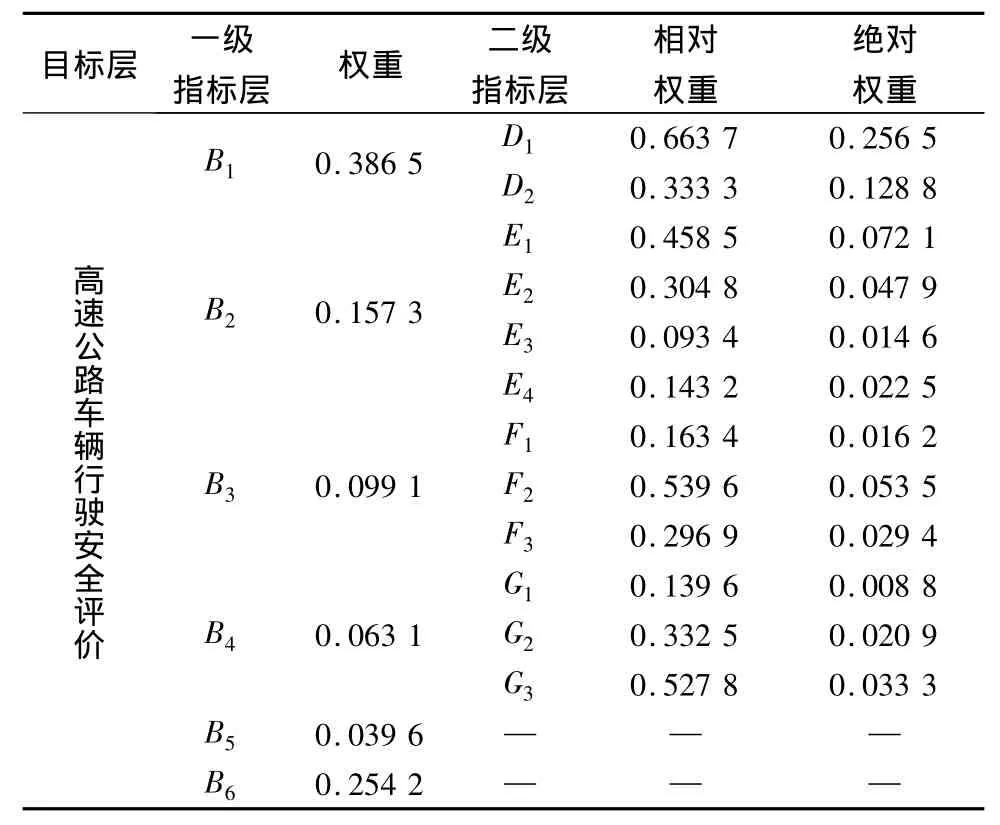
表10 层次总排序计算Table 10 Computation of the total level sorting

5.2 总的评价模型的建立（表11）

表11 各子评价模型Table 11 Each sub-evaluation model

由表3可知，笔者所定义车速离散度分为3个等级，分别对应3个安全水平，假设:

总的行驶安全性评价模型可以写为:

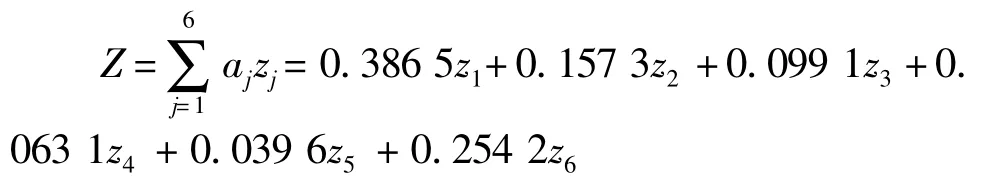
1）当80≤z≤100时，表明车辆行驶很安全;

2）当60≤z≤80时，车辆行驶比较安全;

3）当z≤60时，车辆行驶不安全，系统将交通预警。由于车辆相关参数，车路相关参数，以及道路线形的评分已经确定，此时驾驶员应提高警惕及调整车速，以此来提高车辆行驶安全。

6 指标分值确定

由驾驶员经验对行车安全的影响［12］，将驾驶员经验分为5个级别，生理心理状态分为1～5级，1级代表生理心理状态最佳，2级次之，依次类推;将车辆性能等级、车辆新旧程度、车辆外廓尺寸、车辆质量分为5级;根据道路附着系数与交通事故关系统计，滚动阻力系数与交通事故关系统计，将道路附着系数、横向力系数、滚动阻力系数分为5个级别;根据曲率与交通事故关系统计，高速公路坡度与事故率关系的统计资料［12］以及高速公路不同路段平曲线半径与对应的平均亿车事故率的统计分析结果［12］，将曲率、曲线坡度、曲线半径分为5个级别，这些分级指标相对应一定的评分标准，见表12。

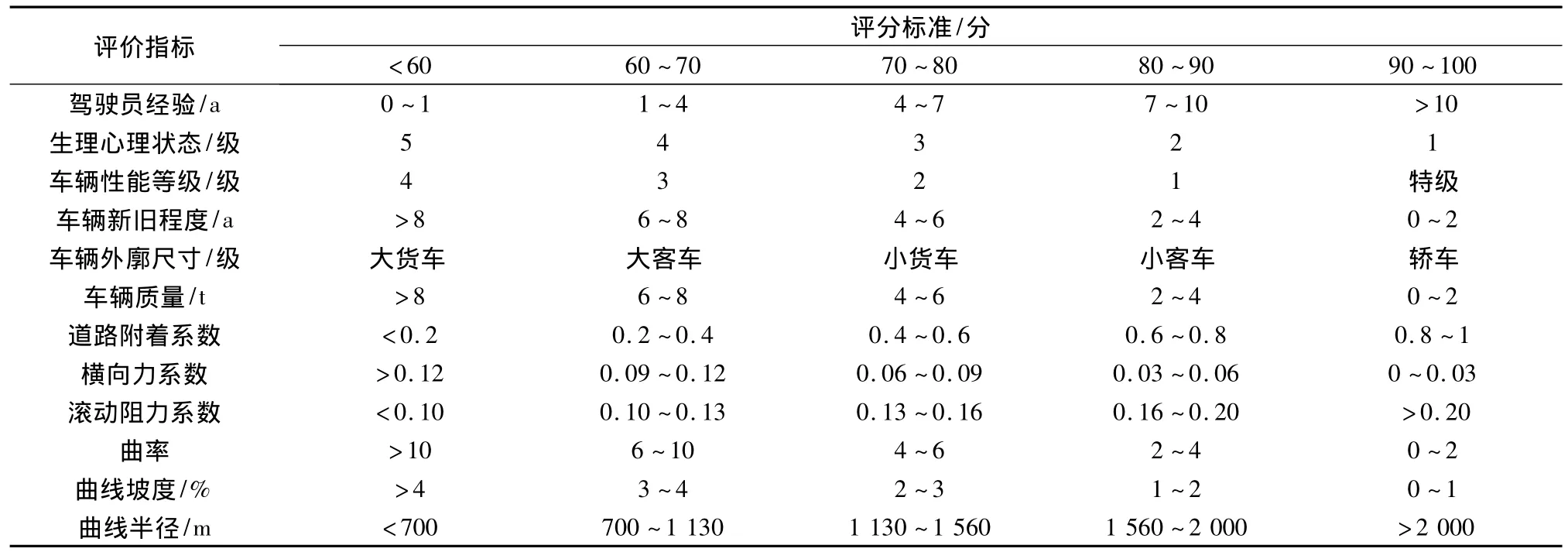
表12 车辆行驶安全评价指标分值确定Table 12 Traffic safety evaluation index score

7 模型验证

2006-07 -20 T 09:45，天气晴朗，一辆奥迪轿车行至京福高速（设计速度100 km/h）269 km+900 m时单车发生事故，造成车上一名乘客死亡，车辆严重损坏。该路段为南北走向，平坦沥青路面，双向4车道，中间用隔离带分离，行车道宽度分别为340 cm，375 cm。

事故原因分析有两点:①轿车的轮胎裂口周围橡胶老化，从内测检查裂口，发现周围有明显的压痕，并且轮胎在轿车与护栏接触前已经爆裂;②根据现场勘查车速鉴定结论为171 km/h，存在明显超速行为，指标具体评分见表13。

表13 实例评价Table 13 Example evaluation

综上所得，模型所得分为53.569分，由模型可知，车辆行驶不安全，这与客观发生情况是相符的。

8 结语

提出了基于速度离散度的车辆行驶状态评分标准，运用层次分析法对一级指标的评价模型权重系数进行了计算，并评价了模型的权重系数，通过了一致性检验，得到了总的高速公路车辆行驶安全评价模型。通过车辆行驶状态评分标准模型，可更加有效地实施交通预警，从而对不安全路段进行优化道路设计，对高速公路行车安全质量的提高有重要意义。

（References）:

［1］ JTGB 01—2003公路工程技术标准［S］.北京:人民交通出版社，2003.

［2］ 姚红云，黄键，蒙井玉.基于模糊数学的山区道路安全度模型评价［J］.交通信息与安全，2010（5）:82-85.

Yao Hongyun，Huang Jian，Meng Jingyu.Mountain road safety evaluation model based on the fuzzy mathematics［J］.Journal of Transport Information and Safety，2010（5）:82-85.

［3］ 潘艳荣，翟长旭，朱顺应.基于灰色聚类理论和人工神经网络技术的道路交通安全评价［J］.重庆交通学院学报，2005，24（2）:101-105.

Pan Yanrong，Zhai Changxu，Zhu Shunying.An evaluation of the road traffic safety based on the grey cluster and neural network［J］.Journal of Chongqing Jiaotong University，2005，24（2）:101-105.

［4］ 周俊昌，常玉林，郭敏.基于交通冲突技术的高速公路安全评价［J］.重庆交通大学学报:自然科学版，2011，30（5）:974-982.

Zhou Junchang，Chang Yulin，Guo Min.Safety evaluation of highway based on the traffic conflict technique［J］.Journal of Chongqing Jiaotong University:Natural Science，2011，30（5）:974-982.

［5］ Miaou S P，Lum H.Modeling vehicle accidents and expressway geometric design relations［J］.Accidents ＆ Prevention，1993，25（6）:689-709.

［6］ Hashemi R R.Neural network for transportation safety modeling［J］.Expert Systems with Appications，1995，9（3）:247-256.

［7］ Solomon D.Accidents on Main Rural Highways Related to Speed，Drivers，and Vehicle［R］.Chicago:Bureau of Public Roads，Department of Commerce，1964.

［8］ 杜博英.道路交通事故与车速建模［J］.公路交通科技，2002（6）:116-118.

Du Boying.Expressway traffic accident and matrix of vehicle speed［J］.Journal of Highway and Transportation Reseach and Development，2002（6）:116-118.

［9］ 王昊.普通公路车速离散性与交通流微观特性关系研究［D］.南京:东南大学交通学院，2007.

［10］裴玉龙，程国柱.高速公路车速离散性与交通事故的关系及车速管理研究［J］.中国公路学报，2004，17（1）:74-78.

Pei Yulong，Cheng Guozhu.Research on the relationship between discrete character of speed and traffic accident and speed management of freeway［J］.China Journal of Highway and Transport，2004，17（1）:74-78.

［11］赵焕臣，许树柏，和金生.层次分析法:一种简易的新决策方法［M］.北京:科学出版社，1986.

［12］沈斐敏.道路交通安全［M］.北京:机械工业出版社，2007.

Analysis of Traffic Safety Evaluation Model for Expressway

Zhao Yuan，Yao Hongyun，Yan Dongmei，Long Donghua
（School of Traffic＆ Transportation，Chongqing Jiaotong University，Chongqing 400074，China）

Highway traffic safety score model is established to more effectively carry out a real-time traffic warning.A new definition of the speed dispersion is introduced to analyze the relationship between the new definition of speed dispersion and conventional dispersion-standard deviation of speed，which indicates a function relationship between the two.Factors such as speed dispersion，driver，road，vehicle and climate，constitute six major indicators of the driver-vehicle-road-the road alignment-climate-vehicle status;the sub-indicators of the major indicators are selected;a corresponding evaluation index system is established.The weight of each parameter is calculated to build the model by AHP.After being verified by example，it is indicated that the model is in line with objective reality，therefore it has certain feasibility.

highway;speed dispersion;AHP;safety score model

U491.2

A

1674-0696（2012）04-0846-06

10.3969/j.issn.1674-0696.2012.04.27

2011-07-25;

2012-04-18

国家自然科学基金项目（51008321）

赵 圆（1987—），男，江苏南通人，硕士研究生，主要从事交通运输规划与管理方面的研究。E-mail:haoyuan26@163.com。