基于相关向量机的中长期径流预报模型研究

仕 玉 治， 彭 勇， 周 惠 成

（1.大连理工大学 水利工程学院，辽宁 大连 116024；2.山东省水利科学研究院，山东 济南 250013）

0 引 言

中长期径流预报对统筹安排防洪与抗旱、水库调度与管理等事务，实现水资源的最大利用效益具有十分重要的实践意义.由于水文系统本身的非线性及水文要素变化的不确定性，目前基于严密的物理方法还很难对径流等水文现象进行描述和预测，人们主要借助于成因分析法、水文统计法、模糊分析等方法来描述和预测水文过程.水文统计法依据水文资料的统计规律进行预测，方法较为常用，它包括两大类：一类是分析水文要素自身随时间变化的统计规律，并建立模型进行预测，如时间序列分析法；另一类是分析水文要素与多因子之间的相关关系，建立模型进行预测，如多元回归法.两类均可直接利用原序列建立线性或非线性关系进行预测，但其精度有时不能满足工程需要.相空间重构成为分析时间序列的一种崭新的方法，通过挖掘或者恢复水文系统的多变量影响因子，重构水文非线性动力系统，国外许多学者对短期径流预报进行研究，并取得了较好的应用效果[1、2].时间滞时τ和嵌入维数m（文中也称重构参数）对时间序列的噪声和数据量大小等影响因素比较敏感[3]，通常采用互信息法、关联维数法、虚假近邻法和Cao法等多种方法所得到的估计值差别较大，不利于获得较好的预报精度.本文采用 Yu等[4]和Sivakumar[5]提出的方法，优化得到重构参数.

一般线性方法难以描述水文系统非线性特征，许多新的方法逐步被引用到水文预报模型当中，如贝叶斯理论、人工神经网络（ANN）、支持向量机（SVM）等[2、6、7]，进一步发展了非线性径流预报模型.2000年Tipping提出了一种新的稀疏概率模型相关向量机[8]（relevance vector machine，RVM），该方法用非线性核函数映射到高维空间，在高维空间进行线性回归，成功实现非线性向线性转化，同时基于贝叶斯理论定义模型参数，不仅可以定量预报，而且能够以概率分布的形式描述水文预报不确定度，可为水库调度决策分析提供更多的可利用信息.目前，其已应用到图像分析[9、10]、信道均衡[11]等分类与回归问题，获得了较好的应用效果.

综上所述，确定自身前期影响因子和建立预报模型，是时间序列分析预测方法的关键，本文首先对径流时间序列进行相空间重构，挖掘水文系统多变量因子；然后利用重构后的时间序列建立RVM非线性径流预报模型，并采用粒子群优化（PSO）算法[12]辨识模型参数；最后应用实例验证本文模型的有效性.

1 混沌时间序列相空间重构

相空间重构是混沌理论的基础，依据Takens理论[13]，对某一混沌时间序列｛xi：i＝1，2，…，n｝，只要适当选取时间滞时τ和嵌入维数m，且嵌入维数满足m≥2D＋1，其中D为饱和关联维数，即可重构与原未知动力系统具有相同几何特征的m维相空间，则相空间中的点可以表示为Xi＝（xixi＋τxi＋2τ…xi＋（m－1）τ）T，由N个相点组成的延迟状态向量表示为｛Xi：i＝1，2，…，N｝，其中N＝n－（m－1）τ，则相应关联积分表达式为

对于混沌时间序列，关联积分C（r，m）与标度尺度r近似成指数关系：C（r，m）∝rD，

2 相关向量机（RVM）径流预报模型

已知相关向量｛Xi：i＝1，2，…，N｝，给定任意一个输入向量X＊，则通过非线性映射到高维特征空间，然后在高维特征空间中进行线性回归得到预报输出值，即RVM的模型输出表示为

式中：K（·，·）为核函数，w为模型的权值.

式中：y＝ （y1y2…yN）；w＝ （w0w1…wN）；Φ为N×（N＋1）核函数矩阵，Φnn＝K（Xn，Xn），Φn1＝1.利用极大似然函数法估计w、σ时会导致严重的过拟合现象[8]，因此，为每个w定义高斯先验概率分布函数

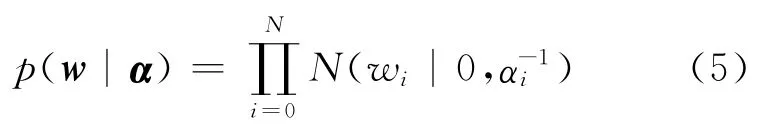
然后基于贝叶斯准则计算权值的后验概率分布，即

式中：后验分布的协方差和均值分别为Σ＝

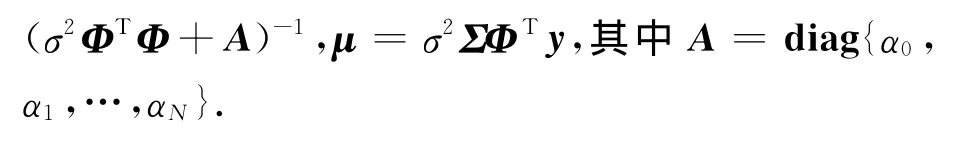
通过最大化边缘似然分布函数

即可得超参数估计值，本文采用EM算法[8]内循环迭代估计超参数α、σ，其αi和σ的迭代方程分别如下：

式中：γi＝1－αiΣii.

3 模型参数辨识及计算流程

RVM径流预报模型需要解决两个问题：（1）模型核函数选择；（2）模型参数辨识过程中的目标函数确立.对于核函数的选择，线性核函数是径向基核函数的特例，特定的sigmoid核函数功能上与径向基核函数相同，核函数自身参数的个数太多不利于参数的选择[7]，因此，本文选取径向基核函数为核函数；其次，在模型参数识别过程中，通常选取训练样本的拟合误差最小为模型目标函数，但是该方式下训练误差收敛过程中会出现严重的过拟合现象，如图1中拟合曲线1所示，训练阶段拟合误差非常小，几乎接近于零，导致优化参数不合理，外推期预报精度非常低.因此本文在训练过程中考虑具有丰、平、枯年份的检验样本误差来抑制过拟合，即综合考虑训练样本和检验样本的误差建立目标函数，如下式：

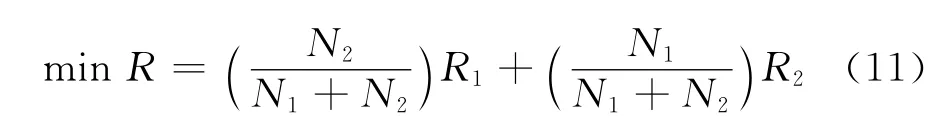
式中：R1、R2分别为训练期、检验期的相对误差绝对值的平均值，N1、N2分别为训练期、检验期的样本个数.其收敛过程如图1中拟合曲线2所示，曲线2的收敛值要比曲线1的收敛值大，说明本文目标函数具有抑制过拟合的能力.

最后，利用RVM模型进行径流预报的主要步骤如下：

（1）给定参数m、τ、ε的合理取值区间，对时间序列进行相空间重构；

图1 不同目标函数的训练误差收敛过程Fig.1 Training error convergence process of different objective functions

（2）利用重构后的训练样本作为RVM的输入进行训练，采用PSO算法辨识方法参数，并验证数据序列的混沌特性，在RVM内循环中，利用式（8）、（9）迭代估计超参数αi、σ，给定一个αmax的值，将对应的权重值设定为0，并剔除对应的Xi，所剩余的X即为相关向量，对应的权重向量

（3）依据优化所得参数为模型的参数取值，给定任意一个输入向量X＊，采用训练好的RVM进行计算便可得到预报值的均值μ＊和方差，预报值服从均值μ＊和方差的后验正态概率分布.

4 应用实例分析

选取南方两水库入库月径流时间序列作为研究实例，分别为水库1的51a（1953－01～2003－12）和水库2的48a（1958－01～2005－12）入库月径流时间序列.水库1的控制流域面积为11.45×104km2，多年平均月径流量为1 251m3/s，变差系数为0.717，最大、最小月径流量分别为5 000、248 m3/s；水库2的控制流域面积为10.26×104km2，多年平均月径流量为1 215m3/s，变差系数为0.856，最 大、最 小 月 径 流 量 分 别 为 5 480、236 m3/s.每一个样本序列分成3个子样本，对于水库1，将前41a资料作为模型的训练样本，中间包含丰、平、枯年份的5a资料作为检验样本，与前41 a配合确定合理的模型参数，剩余5a不参加确定模型参数，纯粹用于检验确定模型的外推预报能力.同样，对于水库2，用前38a的序列点作为训练样本，中间5a作为检验样本，剩余5a序列点作为外推预测样本.对数据进行规格化处理，采用PSO算法优化各方法中的参数，取相对误差的绝对值（Emar）、相关系数（R）、确定性系数R2和合格率（定量）作为预报结果的评价指标.先以水库1为例进行计算分析，以水库2作进一步的验证.

4.1 实例分析

RVM模型参数主要有相空间重构参数（m、τ）、所选取的核函数自身参数及模型自动确定的超参数（α，σ）.给定一个较小的参数区间，进行优化计算，若优化所得参数值为区间端点值，则进一步扩大区间重新计算，直至参数取值在区间范围内为止，即该区间为参数区间，由此确定径向基核函数带宽ε，混沌时间序列嵌入维数m、时间滞时τ的取值区间分别为[0.1，100]、[1，20]、[1，10]，另外对超参数初始化，取α（0）＝（0.25，0.25，…，

其次，对时间序列进行相空间重构，以重构后的训练样本作为径流模型的输入条件，采用PSO优化模型参数（ε、m、τ），水库1结果为（2.172 3，14，4），水库2结果为（4.554，7，6）.根据优化所得时间滞时，分别以嵌入维数m＝1～20绘制D－log2r折线斜率图，如图2所示，log2r在1～2，且m＞8时饱和关联维数趋于稳定值，即存在显著标度区，从而可以定性判断两水库月径流序列存在混沌特性，并由图2（a）、（b）可以估计出1＜D＜3，重构参数m满足m≥2D＋1的条件，说明重构参数是合理的.此外，在参数内循环过程中，随着超参数的迭代估计，边缘似然分布函数值逐步趋于稳定，如图3所示；由图4知超参数σ2收敛很快，迭代3次后基本达到最优值，因此有的文献也将超参数σ2作为一个固定值进行内循环计算.

图2 水库1和2月径流关联维数图Fig.2 Correlation dimension of monthly runoff flow of Reservoirs One and Two

图3 log2（p（y｜α，σ2））的收敛过程Fig.3 Convergence process of log2（p（y｜α，σ2））

图4 超参数σ2的收敛过程Fig.4 Convergence process of hyper－parameterσ2

分析模型的模拟、检验、外推预报精度，并将本文模型（RVM）与应用较为广泛的最小二乘支持向量机模型（LSSVM），以及未考虑相空间重构的（m＝12，τ＝1）相关向量机模型（RVM＊）和自动回归滑动平均模型（ARMA（5，6））进行对比分析.计算结果列于表1中，RVM方法对于训练期、检验期和外推预测期的预报结果见图5～8.

总体而言，由表1知，考虑相空间重构进行预报时比未考虑相空间重构时，RVM获得比单一方法更优的预报精度，与LSSVM和ARMA（5，6）的计算结果相比较，RVM的评价指标值均优于其相应值，说明RVM具有较好的预报性能.按照《水文情报预报规范》（SL 250—2000）标准将径流量划分为枯、偏枯、平、偏丰、丰5个级别，对高流量（包括偏丰和丰流量）精度进行了定量、定性比较分析，结果如表2所示.RVM在训练期、检验期及外推预测期的平均绝对相对误差分别比LSSVM和ARMA的相应值要小，但同时其预报精度均比预报总体时相应值低，以多年变幅的20%为许可误差，比较分析知，其定量合格率较本文所列其他方法有所提高.为提供更为充分的预报信息，本文对比分析了三阶段高流量的定性预报合格率，除了在检验期RVM和LSSVM的合格率相同以外，其余两阶段RVM均获得比其他方法更高的定性预报合格率，同样说明RVM具有较强的高流量预报能力.

表1 水库1月流量不同方法预测精度Tab.1 Prediction accuracy of monthly flow of Reservoir One resulting from various methods

图5 训练期流量实测值与RVM预报值对比图及相关图Fig.5 Comparison and scatter plot between observed flow and predicted flow by RVM during training period

图6 检验期流量实测值与RVM预报值对比图及相关图Fig.6 Comparison and scatter plot between observed flow and predicted flow by RVM during test period

图7 外推预测期流量实测值与RVM预报值对比图及相关图Fig.7 Comparison and scatter plot between observed flow and predicted flow by RVM during validated period

图8 外推预测期实测流量与RVM预报区间对比图Fig.8 Comparison between observed and predicted interval hydrograph during validated period

进一步考虑径流预报的不确定性，以预报值的均值和方差为预报的后验概率分布函数来描述预报值的不确定性，并讨论了发生概率为80%的区间预报，其区间预报结果及实测流量过程如图8所示.由图8知，中低流量预报区间基本上可以包住实测流量，高流量区间上下限值对应的级别能够预报出实测值对应的级别，概率区间预报是可靠的.

4.2 实例验证分析

水库2的统计参数与水库1基本相同，但是变差系数较大，数据序列平稳性相对较差，在同样可行条件下，对水库2进行了计算，其预报结果的评价指标列于表3.由表3知，RVM较LSSVM和ARMA（6，6）模型具有较高的预报精度，验证说明了本文模型的有效性.

表2 水库1高月流量不同方法预测精度Tab.2 Prediction accuracy of high monthly flow of Reservoir One resulting from various methods

表3 水库2月流量不同方法预测精度Tab.3 Prediction accuracy of monthly flow of Reservoir Two resulting from various methods

5 结 论

（1）将混沌技术与相关向量机结合建立径流预报模型，采用PSO算法辨识模型参数，优化所得重构参数满足混沌理论条件，耦合方法比单一方法的预报精度有所提高，并对总体和高流量值进行分析，取得比LSSVM和ARMA模型更优的预报精度，说明本文模型的有效性.

（2）相关向量机为概率模型，能够定量地、以概率分布的形式描述径流预报不确定性，并给出指定发生概率下的区间预报.

（3）在进行中长期径流预报应用时，相关向量机模型的不足之处是模型参数和样本序列均以正态概率分布函数进行推理，但从模型计算的结果来看可用于中长期径流预报，下一步将以P－Ⅲ型概率分布函数进行模型研究.

[1] SIVAKUMAR B. Chaos theory in hydrology important issues and interpretations[J].Journal of Hydrology，2000，227：1－20

[2] SIVAKUMAR B， JAYAWARDENA A W，FERNANDO T M K G.River flow forecasting：use of phase－space reconstruction and artificial neural networks approaches [J].Journal of Hydrology，2002，265：225－245

[3] 王 文，许武成.对水文时间序列混沌特征参数估计问题的讨论[J].水科学进展，2005，16（4）：606－610

[4] YU X Y，LIONG S Y，BABOVIC V.EC－SVM approach for real time hydrologic forecasting [J].Journal of Hydroinformatics，2004，6（3）：209－223

[5] SIVAKUMAR B.Nonlinear determinism in river flow prediction as a possible indicator [J].Earth Surface Processes and Landforms，2007，32：969－979

[6] LIONG S Y，SIVAPRAGASAM C.Flood stage forecasting with SVM [J].Journal of the American Water Resources Association，2002，38（1）：173－186

[7] 林剑艺，程春田.支持向量机在中长期径流预报中的应用[J].水利学报，2006，37（6）：681－686

[8] TIPPING M E.The relevance vector machine[J].Advances in Neural Information Processing System，2000，12：652－658

[9] AGARWAL A，TRIGGS B.3Dhuman pose from Silhouettes by relevance vector regression[J].Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2004，2：882－888

[10] BOWD C，MEDEIROS F A，ZHANG Zuo－hua，etal.Relevance vector machine and support vector machine classifier analysis of scanning laser polarimetry retinal nerve fiber layer measurements[J].Investigative Ophthalmology ＆ Visual Science，2005，46：1322－1329

[11] CHEN S，GUNN S R，HARRIS C J.The relevance vector machine technique for channel equalization application [J].IEEE Transactions on Neural Networks，2002，12（6）：1529－1532

[12] KENNEDY J，EBERHART R C.Particle swarm optimization[C]//Proceedings of IEEE Conference on Neural Networks.Piscataway：IEEE Press，1995：1942－1948

[13] KANTZ H，SCHREIBER T.Nonlinear Time Series Analysis [M].Cambridge：Cambridge University Press，1997