基于D－H矩阵的球面5R并联机构误差建模及灵敏度分析

李永泉 张立杰 郭志民 郭 菲

燕山大学，秦皇岛，066004

0 引言

按照机构误差源分类，机构误差包含原理误差、制造误差、使用误差、测量误差［1］，而并联机器人机构的主要误差来源取决于制造误差［2］，即各主要零部件加工、装配误差，这些误差是导致球面机构各转动副轴线和球心之间产生偏差的主要原因。球面机构的特点是各转动副轴线汇交于一点（球心），以保证输出精度，如果汇交偏差过大，球面机构就演变成为普通的空间机构，失去了球面机构特性。为此，减小各转动副轴线和球心之间的偏差至关重要，但相关的研究文献很少。文献［2］利用空间矢量链分析法研究了3－RRR并联数控回转台的精度分析问题，文献［3］利用微分法建立了3－RRR拟人肩关节的几何误差模型，但文献［2－3］只分析了球面机构的姿态误差，没有对其进行相应的位置误差分析，同时也没有考虑球面机构各转动副轴线和球心之间的偏差，而该误差在实际的球面机构加工和装配过程中是不可避免的。为此，本文基于D－H参数，采用环路增量法［1］对球面5R并联机构进行误差分析，同时得到了球面机构的位置误差和姿态误差模型，最后进行了灵敏度分析。

1 球面5R并联机构简介

球面并联机构中最简单的结构形式是球面二自由度5R并联机构，它具有重要的实际应用价值，如作为球面上点的定位设备［4－5］以及卫星信号自动跟踪设备［6］等。

如图1所示，该并联机器人选取广义参考点P作为输出，具有沿球面曲线移动的2个自由度，它通过2个串联3R运动链分支PB1A1、PB2A2与固定平台弧A1A2连接，该机构所有运动链的转动副轴线皆汇交于球心O点。各转动副轴线间夹角（即第i连杆圆心角）分别为αi（i＝1，2，…，5），相邻连杆间夹角分别为θi，其中θ1、θ5为驱动角。固连在第i连杆上的局部坐标系（简称i系）原点皆为球心O点，xi轴沿各转动副轴线方向，yi轴位于i连杆所在平面上且在实体杆一侧，zi轴垂直于对应连杆所在平面，构成右手直角坐标系。基坐标系与Ox5y5z5重合。令OP与z5轴夹角为φ，OP在Ox5y5平面上的投影与x5轴正向的夹角为φ。

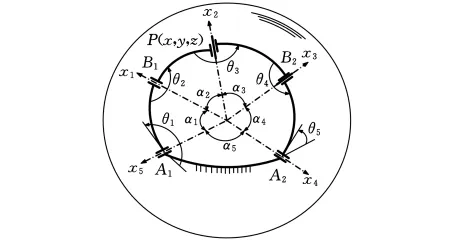
图1 球面5R并联机构

2 误差模型的建立

2.1 结构参数及其几何误差源的确定

采用D－H参数［1］表示球面5R并联机构构件的结构参数，与i连杆相关的D－H参数为转角θi、偏置di、扭角αi、杆长ai，如图2所示。由球面5R并联机构的特点可知，各转动副轴线皆汇交于球心O点，即ai＝0，di＝0，由文献［1］可知，扭角αi即为各连杆对应的圆心角（连杆参数），转角θi即为相邻各连杆间夹角，其中，θ1、θ5为驱动关节运动参量，θ2、θ3、θ4为从动关节运动参量，如图1所示。用dαi表示机构的连杆参数误差，用dθi表示运动参量误差。在实际的球面5R机构中，由于存在加工误差、装配误差，要保证5个转动副轴线精确地汇交于球心O点是不可能的，虽然ai、di的名义尺寸为零，但它们的误差不为零，此处用ddi表示各转动副轴向间隙量，dai表示各转动副轴间距误差（包括各转动副间隙误差），则各转动副轴线和球心之间的偏差由ddi和dai共同体现。

图2 D－H参数图

2.2 基于环路增量法［1］构建误差模型

球面5R并联机构的封闭环方程可以写为

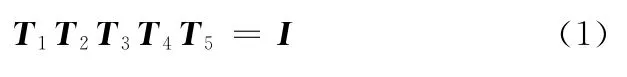
其中，Ti为基于D－H参数的相邻i连杆坐标系之间的变换矩阵，即

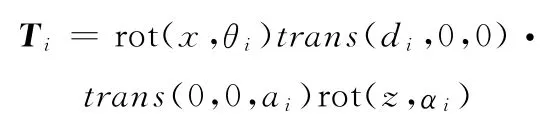
对式（1）进行时间变量微分得

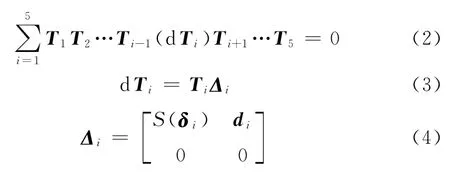
式中，Δi为i连杆在i系中的位姿误差［1］；S（δi）为δi的反对称矩阵［7］；δi为第i连杆相对于自身坐标系的微分转动；di为第i连杆相对于自身坐标系的微分平动。

将式（3）代入式（2），联立式（1）整理后得

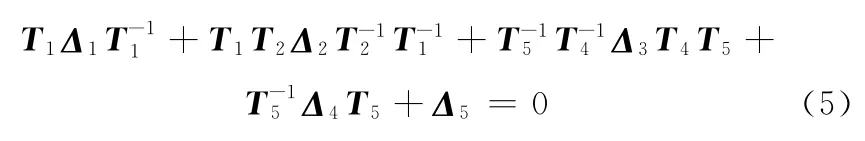
式（5）中各项对应元素之和为零，等价于下列两个矢量方程：

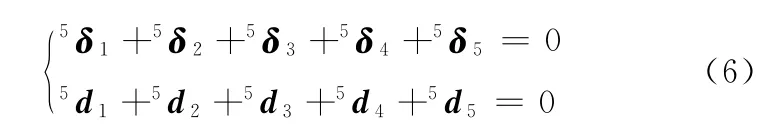
式（6）即为该机构误差模型，其中，各项元素均对应基坐标系下的位置误差和姿态误差，右下标对应i连杆，左上标对应基坐标系，即Ox5y5z5。式（6）中包含已知原始误差为：驱动关节 运 动 参 量 误 差dθ1、dθ5，驱 动 副 轴 向 间 隙量dd1、dd5，连杆参数误差dαi及各转动副轴间距误差dai；包含未知误差为：从动关节运动参量误 差dθ2、dθ3、dθ4， 被 动 副 轴 向 间 隙量dd2、dd3、dd4。进一步由式（6）利用 Maple软件编程可分别求出从动关节运动参量误差dθ2、dθ3、dθ4， 被 动 副 轴 向 间 隙量dd2、dd3、dd4显式函数关系。

在实际的球面5R并联机构中要保证5个转动副精确地汇交于一点是不可能的，即各转动副应配有适当的轴向间隙量，现将dd2、dd3、dd4的显式函数关系式导出，即

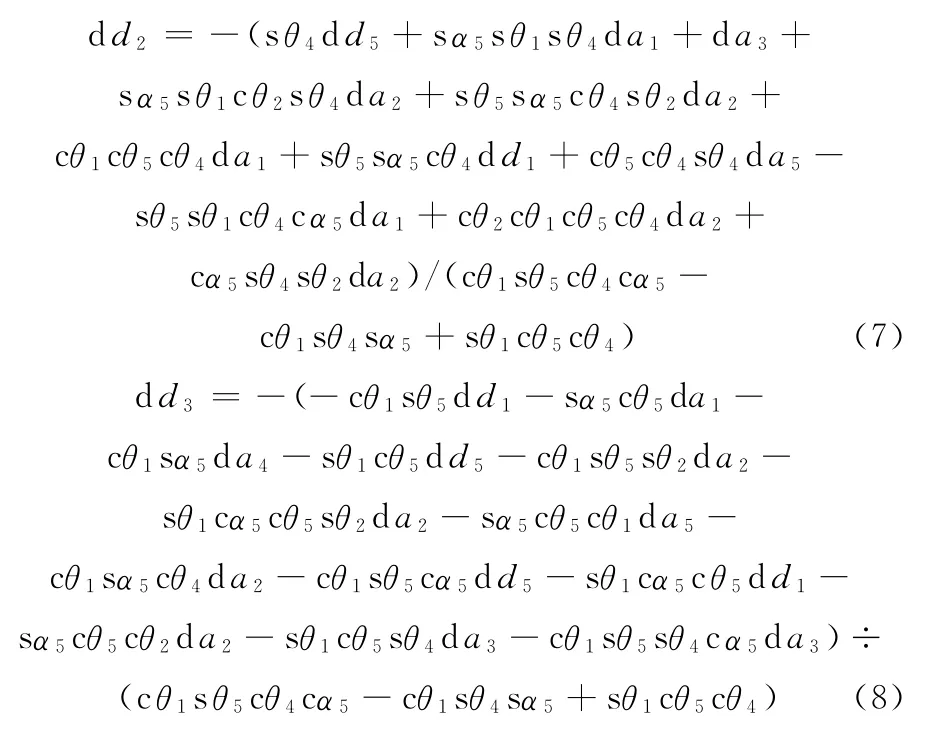
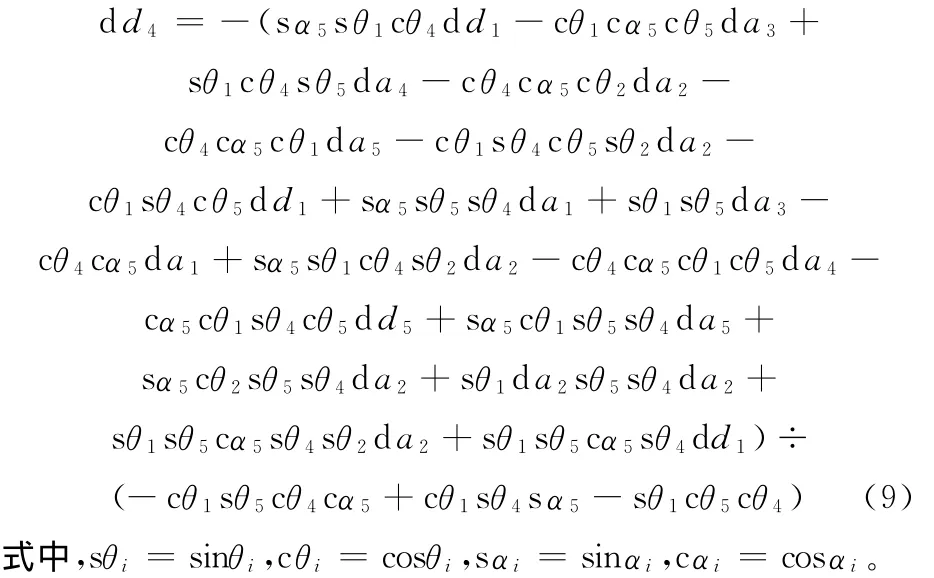
为保证球面5R并联机构平稳运行，要求轴向间隙量ddi和轴间距误差dai之间应满足式（7）～式（9），否则，过小的轴向间隙量将会使机构卡死，而过大的间隙又会导致机构过低的机构精确度。

2.3 末端执行器位姿误差计算模型

在图1中，P点作为输出，固连于第2连杆，位于2系z轴上，d2、δ2分别为第2连杆相对于自身坐标系的微分平动和微分转动，由文献［1］可以得到，第2连杆在2系中的原始误差和第2连杆在基坐标系中的位姿误差之间的关系为

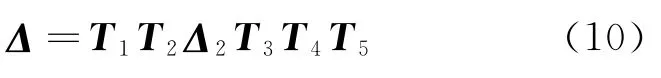
其中，Δ2为第2连杆在2系中的原始位姿误差，由式（4）定义；Δ为第2连杆在基坐标系中的位姿误差，即

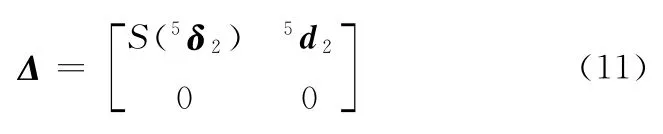
3 精度分析

3.1 精度预估

对于图1所示的球面5R并联机构，取结构参数为α1＝α2＝α3＝α4＝90°，α5＝120°。取运动特性［8］较好的工作空间0°≤φ ≤30°，0°≤φ ≤360°。

（1）位置精度。由式（10）可知，机构末端执行器的位置精度仅与轴间距误差dai和轴向间隙量dd1、dd5有关。此处，驱动副（即电机轴）位于机座上，其轴向间隙量dd1、dd5由镗床加工精度保证，可忽略不计。

为了评价该机构末端执行器的位置精度，定义其位置误差为

为了找出末端执行器位置误差在所选取工作空间区域内的分布规律，根据三维坐标测量仪测量样机尺寸所得结果，选取轴间距误差dai绝对值均为0.1mm，对其进行正负组合，共有32种情况，借助MATLAB软件，计算机构末端执行器位置误差。通过所有情况比较可知，表1所示第1组误差值引起的末端执行器位置误差最小。本文只以表1所示两组误差值为例，分别绘制末端执行器位置误差在所选取工作空间区域内的分布规律，如图3所示。可以得出结论，装配机构时，轴间距误差按第1组误差情况进行分配比较合理。

表1 机构各转动副轴间距误差 mm

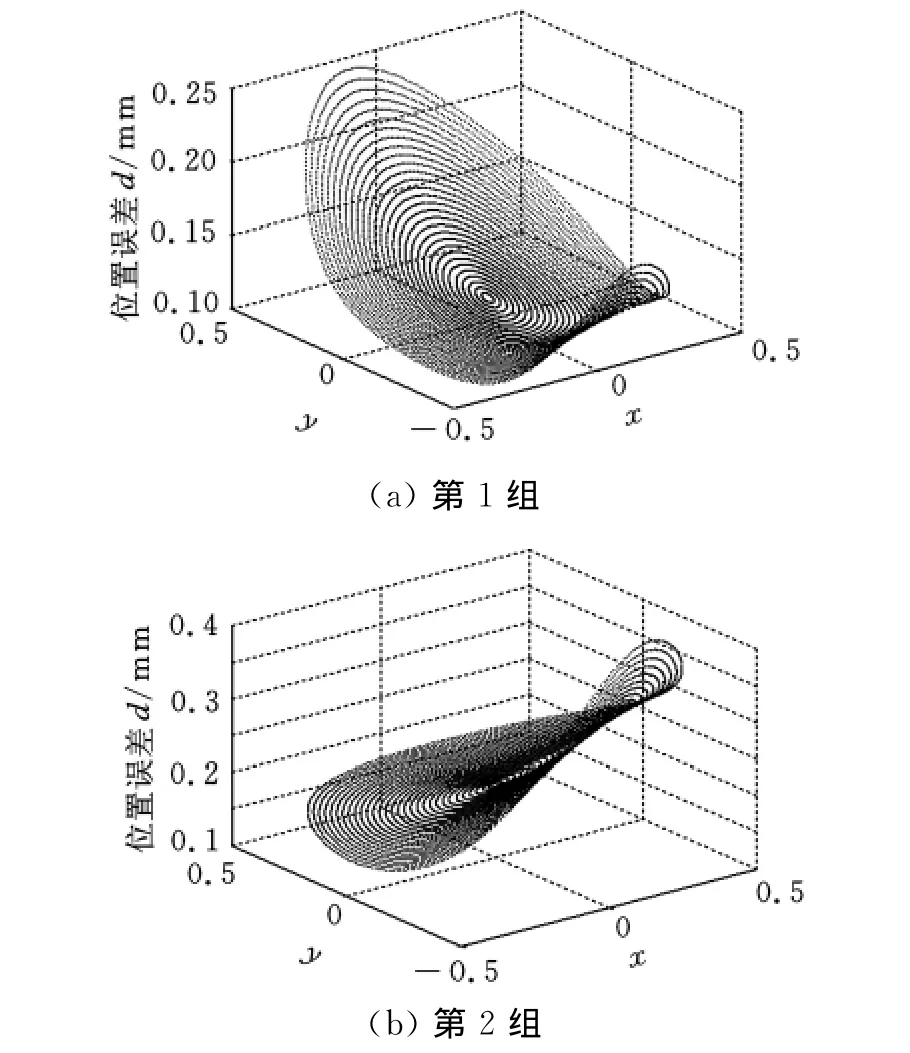
图3 末端执行器位置误差分布规律

（2）姿态精度。由式（10）可知，机构末端执行器的姿态精度仅与连杆参数误差dαi和驱动关节运动参量误差dθ1、dθ5（由控制方法保证，此处忽略）有关。为了评价该机构末端执行器的姿态精度，按文献［2-3］定义其姿态误差为

为了找出末端执行器姿态误差在所选取工作空间区域内的分布规律，根据三维坐标测量仪测量样机尺寸所得结果，选取连杆参数误差dαi绝对值均为0.1°，对其进行正负组合，共有32种情况，借助MATLAB软件，计算机构末端执行器姿态误差。通过所有情况比较可知，表2所示第1组误差值引起的末端执行器姿态误差最小。本文只以表2所示两组误差值为例，分别绘制末端执行器姿态误差在所选取工作空间区域内的分布规律，如图4所示。可以得出结论，装配机构时，结构参数误差按第1组误差情况进行分配最合理。

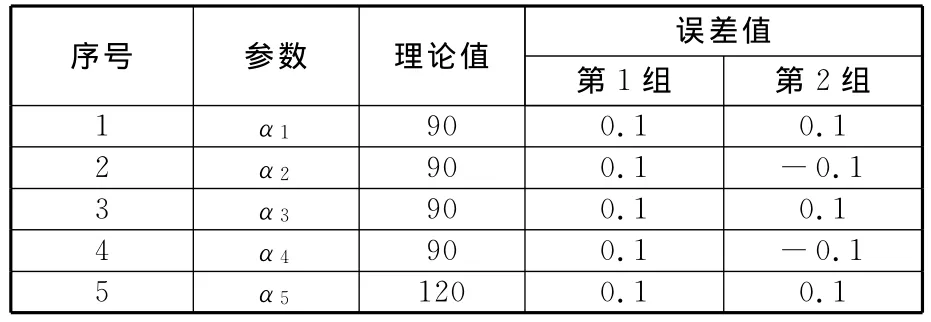
表2 机构结构参数理论值与误差值 （°）

图4 末端执行器姿态误差分布规律

3.2 误差灵敏度分析

通过上述分析可知，对应不同组的设计参数，即使在相同的输入误差和运动轨迹条件下，机构位姿误差也不相同。灵敏度分析有助于合理选用设计参数，改善机构运动性能，提高机构运动精度，便于在设计机构时，选取对末端执行器位姿误差有重要影响的机构主要设计参数。

（1）位置误差灵敏度分析。为了分析各零部件误差对末端执行器位置误差的影响，定义d关于各项独立位置误差源dai、dd1、dd5的灵敏度系数为

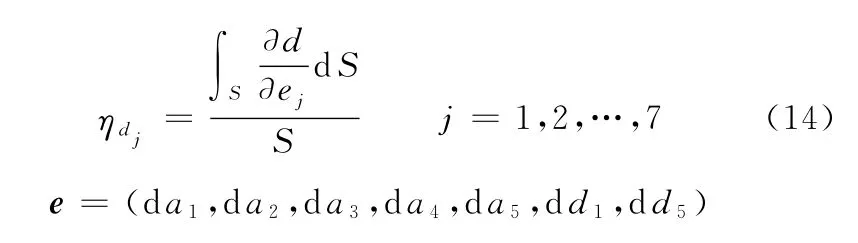
式中，S为球面工作空间面积。

由式（14），借助MATLAB软件，绘制了各误差参数的灵敏度直方图，见图5。由图5可知，7项误差源对末端执行器的位置误差影响均较大。

图5 位置误差灵敏度直方图

（2）姿态误差灵敏度分析。为了分析各零部件误差对末端执行器姿态误差的影响，由文献［9-10］定义δ关于各项独立姿态误差源dαi、dθ1、dθ5的灵敏度系数为

由式（15），借助MATLAB软件，绘制各结构误差参数的灵敏度直方图，见图6。由图6可知，7项误差源对末端执行器的姿态误差影响均较大。

图6 姿态误差灵敏度直方图

4 抑制末端位姿误差加工装配工艺设计

为控制球面5R并联机构姿态误差，4个连杆可以通过线切割的方式一次成形，以保证结构参数误差即dα1、dα2、dα3、dα4的一致性；为控制球面5R并联机构位置误差，选好机构加工和标定基准以后，通过镗床加工与电机轴相连的机架上的两个轴承座上的孔，严格按120°分布，精度由镗床保证，这样可保证dd1、dd5在允许范围内，同时保证结构参数α5的精度；为保证球面5R并联机构平稳运行，要求被动副轴向间隙量应满足式（7）～式（9），为此在各转动轴承处设置调整垫，并根据式（7）～式（9）计算结果进行配磨，使得误差被控制在允许范围内。在该机构进行装配时，设置专门卡具，以尽量保证各转动副轴线同球心。

5 结论

（1）在结构参数误差基础上，综合考虑轴向间隙量和轴间距误差，基于环路增量法，建立了球面5R并联机构位置和姿态误差模型并显式给出，更接近于工程实际。（2）通过精度分析可知，球面机构位置误差仅与驱动副轴向间隙量和轴间距误差有关，姿态误差仅与结构参数误差和驱动关节运动参量误差有关。（3）定义了位置误差灵敏度系数，通过灵敏度分析可知，各项位置误差源、姿态误差源对球面机构末端执行器位置误差、姿态误差影响均较大。（4）为确保球面5R并联机构平稳运行，要求被动副轴向间隙量应满足式（7）～式（9），以避免该机构出现卡死现象。

［1］ 石则昌，刘深厚.机构精确度［M］.北京：高等教育出版社，1995.

［2］ 曾宪菁，黄田，曾子平.3－RRR型数控回转台的精度分析［J］.机械工程学报，2001，37（11）：42－45.

［3］ 李研彪，金振林，计时鸣，等.一种并联机构拟人肩关节的误差分析［J］.应用基础与工程科学学报，2009，17（3）：446－451.

［4］ Ouerfelli M，Kumar V.Optimization of a Spherical Five－bar Parallel Drive Linkage［J］.Transactions of the ASME，Journal of Mechanical Design，1994，116：166－173.

［5］ Tavkhelidze D S，Davitashvili N S.Kinematic Analysis of Five－link Spherical Mechanism［J］.Mechanism and Machine Theory，1974，9：181－190.

［6］ Gosselin C M，Cloutier C，Rancourt D.Kinematic A－nalysis of Spherical Two－degree－of－freedom Parallel Manipulators［C］／／Proceedings of the 1994 ASME Design Technical Conferences.Minneapolis，MN，USA，1994：255－262.

［7］ 熊有伦.机器人技术基础［M］.武汉：华中科技大学出版社，2003.

［8］ 张立杰，李永泉，黄真.球面二自由度5R并联机器人的运动学分析［J］.中国机械工程，2006，17（4）：342－346.

［9］ 李思维，黄田.一种含平行四边形支链的3自由度并联机构姿态精度综合与装配工艺设计［J］.机械工程学报，2003，39（7）：38－42.

［10］ 黄田，李亚，李思维，等.一种三自由度并联机构几何误差建模、灵敏度分析及装配工艺设计［J］.中国科学（E辑），2002，32（5）：628－635.