基于ABAQUS显式动力学的PCB板跌落研究

刘志峰 张敬东 成焕波

合肥工业大学，合肥，230009

0 引言

动载荷是指随时间急剧发生变化或是构件内各质点产生不可忽略的加速度的载荷。单纯采用力学算法计算动载荷的关键点在于冲击动载荷因子的确定，而且只能求解弹性变形的动载荷因子，产生塑性变形时的动载荷因子只能通过实验的方法确定，最终的计算结果与该动载荷因子成正比，该方法不但计算复杂而且结果缺乏准确性［1］。ABAQUS的Explicit求解器主要用于高速碰撞、复杂接触以及材料的失效和退化仿真分析。ABAQUS／Explicit Dynamic分析方法专门用于对高速动力学进行分析，如在进行爆炸分析时，载荷在瞬间增大而且持续时间非常短，精确地捕捉结构响应的应力波是极其重要的，而应力波与系统的最高阶固有频率和最小时间增量步有直接的关系。为了提高产品的性能，近年来有不少企业和研究机构专门对产品进行跌落碰撞研究，这方面的研究主要有：手机外壳耐冲击性能研究［2］，运用跌落分析对电视机等产品包装材料进行优化设计［3－4］，使用 LS－DYNA 显式动力学有限元方法对便携式工具的跌落性能进行研究［5］，优化约束条件提高构件的抗跌落性能研究［6］等。而对于带有质量集中的线路板等电子元器件基本没有人从事研究。本文对ABAQUS／Explicit dynamic算法的理论进行研究，得出材料的刚度、密度等属性与计算精确度和运算时间等各个变量之间的关系；将PCB板上的电子元件简化为三个集中质量块，建立PCB板跌落的有限元模型，并采用惠斯通电桥测量应变法验证有限元模型的准确性；在试验与模拟的基础上研究PCB板的跌落性能。

1 显式动力学理论分析

1.1 求解算法

ABAQUS／Explicit在整个运算过程中采用中心差分算法求解平衡方程，运用动态方程在每个微小的增量步内计算下一个增量步的动态状况。

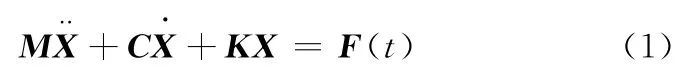
式中，M 为质量矩阵；K为刚度矩阵；C为阻尼矩阵；F（t）为合力，F（t）＝P－I。

对于单个节点，阻尼矩阵和刚度矩阵为零，所以单个节点平衡方程转化为

根据式（1）可计算出节点在t时刻的加速度

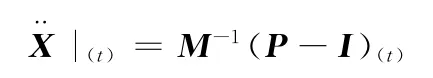
由于显式求解器针对瞬态动力学采用极小的增量步，且质量矩阵全部为对角矩阵而无需求解方程组，节点的加速度完全由质量矩阵和施加在节点上的外力决定，虽然增量步非常小，但是作用时间极短，因此求解过程十分节省资源。

运用中心差分法对加速度积分得出节点的速度方程：

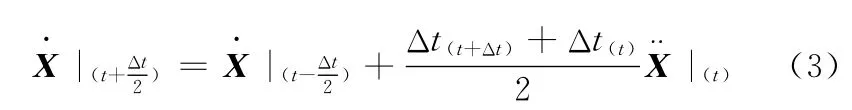
式中，Δt为时间增量步值。

再次运用中心差分法对速度积分求解出位移方程：

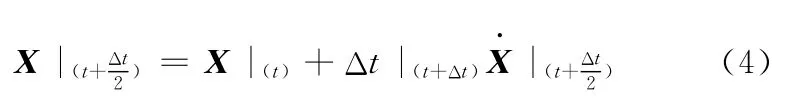
由式（2）～式（4）可知，模型节点的位移、速度和加速度只与时间增量步值有关，因此ABAQUS／Explicit采用极小的时间增量步值和很多的增量步完成中心差分的运算。

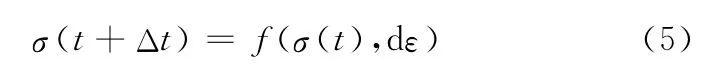
1.2 稳定时间极限Δtstable

ABAQUS／Explicit的算法表明，时间增量步Δt的大小直接关系到计算的准确性，如果该时间大于稳定时间极限Δtstable，则会导致数值不稳定和求解时间无限长，因此在分析之前必须尽可能精确地估算出稳定时间极限。稳定时间极限由系统最高阶频率决定，在无阻尼状态下，有

在有阻尼状态下有

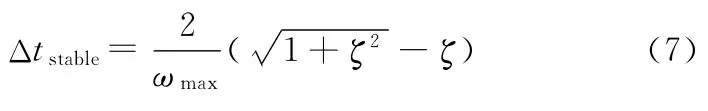
式中，ζ为最高阶频率的临界阻尼系数；ωmax为系统最高阶频率。

要确定系统的最高阶频率必须对系统进行线性摄动分析提取多阶模态值，过程较为复杂。但是系统的最高阶频率与每个单元的最高阶频率紧密相关，并且单元的最高阶频率略高于整体的最高阶频率。为此采用更为简便的方法估算稳定时间极限，即计算每个单元的最高阶频率对应的稳定时间极限：

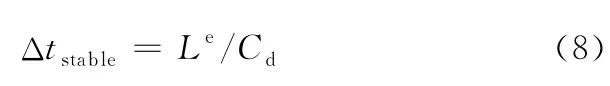
式中，Le为单元在各个尺寸方向上的最小值；Cd为模型材料的波速（这里只适用于弹塑性材料和线弹性材料，超弹性完全不可压缩材料的波速趋近于无穷大）。

由式（8）可以看出，稳定时间极限与单元的最小尺寸成正比，与材料的波速成反比。因而网格越细，所需的稳定时间极限越短，这同时也会使总体分析时间延长。

材料波速的计算公式为

式中，E为材料的弹性模量；ρ为材料的密度。

由此可见，材料刚度越大，波速越大，稳定时间极限越小；而材料的密度越大，波速越小，稳定时间极限越大。增大稳定时间极限有利于分析的顺利进行和数值稳定，同时也使计算的准确性下降，因而在实际运算中可以先估计出稳定时间极限，用较大的时间增量步先进行分析计算，在运算出结果之后再细化网格进行精确运算。

1.3 能量平衡

能量平衡作为后处理的一部分，是评估分析精确性的重要组成部分，通过对比各种能量的比值可以判断分析结果的精确度。

总的能量平衡方程为

式中，EI为内能；EV为黏性耗散能；EFD为摩擦耗散能；EKE为动能；EW为外力做功；EPW为接触罚函数做功；ECW为约束罚函数做功；EMW为质量缩放功；Etotal为总能量。

总能量Etotal为常值的100%，在分析过程中允许的最大误差为1%。验证能量平衡主要是计算伪应变能占总内能的比例，即

式中，EE为可恢复弹性应变能；EP为非弹性（如塑性）耗散能；ECD为蠕变或者黏弹性耗散能；EA为伪应变能。

EA主要是由沙漏因素和壳单元与梁单元的横向剪应变储存的能量，按照ABAQUS／Explicit能量评估的标准，伪应变能占总内能的比例不得高于5%。

2 PCB板跌落分析

2.1 PCB板有限元模型的建立

2.1.1 基本假设

PCB电子元件线路板采用可压缩聚苯乙烯泡沫包装，将PCB板上其他电子元件的质量简化为三个质量块，在距离地面1m高处自由下落，与刚性地面发生碰撞，基本模型如图1所示。本文研究PCB板采用该包装材料是否能承受冲击载荷的作用而不导致材料的断裂失效的问题，为此提出以下几点假设：

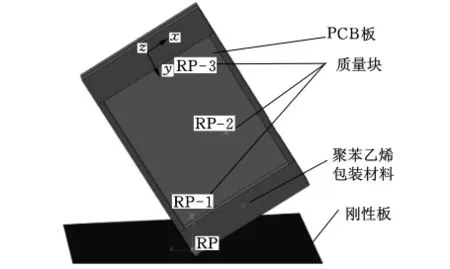
图1 基本模型

（1）电子元件在碰撞过程中无论承受多大的力或者加速度，均不会与PCB板发生分离。

（2）PCB板在跌落瞬间产生的加速度和冲击力不会致使板材发生断裂，在材料定义中也不涉及断裂强度。

（3）尽管跌落时PCB板对包装材料产生很大的冲击力，但并不致使板材进入包装材料内部而使得包装材料破损。

2.1.2 材料定义

（1）刚性板定义为离散刚体，即在PCB板跌落碰撞作用过程中不发生变形。

（2）包装材料为可压缩聚苯乙烯泡沫，其弹性模量为3MPa，泊松比为0，密度为100kg／m3，单轴压缩数据如表1所示。

表1 聚苯乙烯单轴压缩数据

（3）PCB板厚度为4mm，密度为500kg／m3，弹性模量为45GPa，泊松比为0.3。

（4）集中质量块m＝0.5g。

2.1.3 网格划分

首先采用粗网格模型，PCB板网格尺寸为10mm×15mm，单元类型为S4R；刚性板由于已经定义为离散刚体，所以求解精度与网格密度无关，为缩小计算量只划分为一个单元，单元类型为R3D4；包装材料网格尺寸为6.3mm×5mm×3mm，最小单元尺寸为2mm×4mm×6.3mm，单元类型全部为显式线性六面体完全积分单元C3D8R，总体网格数为1618。粗网格模型如图2所示，PCB板的应力分布云图见图3。

图2 粗网格模型

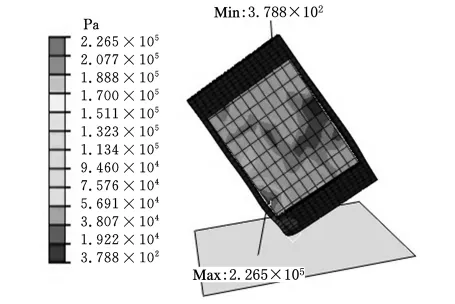
图3 粗网格应力云图

2.1.4 稳定时间极限

根据上述材料属性和网格模型，分别计算不同材料的波速以及由此波速决定的稳定时间极限。

（1）PCB板稳定时间极限

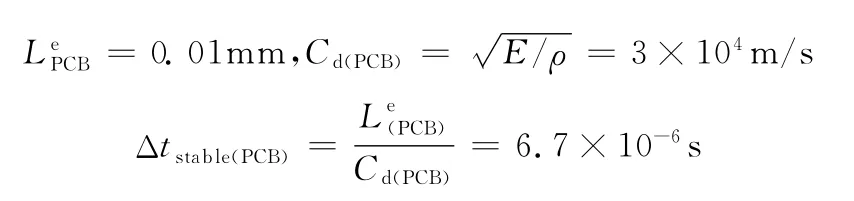
（2）包装材料稳定时间极限

2.2 有限元模型验证

碰撞分析涉及材料非线性和几何非线性因素，且材料非线性影响较为显著。有限元模型的准确性直接关系到后续分析结果的准确性，所以必须通过实验验证所建立的有限元模型准确性。但对于本文所涉及的跌落碰撞过程，很难采用实验检测跌落过程中的力学参数，因此通过静力学实验测试该有限元模型的准确性。以下实验采用应变片测量该包装材料受压情况下的应变情况。

2.2.1 测量方法

利用惠斯通电桥测量电阻应变片的阻值变化来测量应变，将电阻应变片粘贴在图4所示的待测区域，对包装材料的正上部施加500Pa的均布载荷，测量包装材料的4个内角定点和下部中点的应变值，并用有限元模拟相同工况，比较模拟值与测量值的差异。

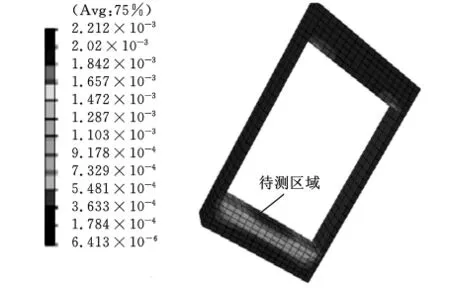
图4 模拟应变

2.2.2 实验结果分析

由表2可看出：有限元模拟结果是，位置1、2的应变值与位置3、4的应变值相等，这与包装材料的结构对称和载荷对称完全一致，位置5的应变值最大；实验值和模拟值的相对误差均在5%以内，也符合ABAQUS显式动力学提出的误差范围。位置1、2的实验值和位置3、4的实验值产生误差的原因有两点：①惠斯通电桥为单臂电桥，一次只能测量一个部位的应变，所以4个位置的应变在理论上虽应相等但由于贴片位置的不精确导致应变值误差；②温度过低致使温度补偿效应减弱，从而使误差增大。

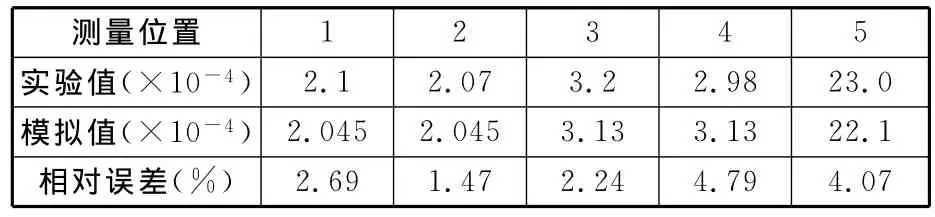
表2 实验值与模拟值（应变）

2.3 跌落模拟结果分析

2.3.1 力学参数分析

由图3可知，PCB板首次与刚性地面发生碰撞时产生的最大应力为226.5kPa，其能量平衡曲线如图5所示，线路板实际能承受的最大压力为36MPa，由于包装材料具有一定的弹塑性，会出现二次回弹跌落，从而引起与刚性地面的多次碰撞，材料的非线性致使黏性耗散能消耗了部分动能，所以以后的跌落产生的应力均小于首次跌落产生的应力，因此确定首次跌落碰撞力为跌落过程中的最大力。据此分析表明，该包装材料完全满足1m高度的跌落安全性能要求。

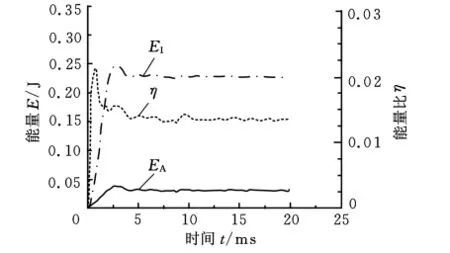
图5 粗网格能量平衡图

2.3.2 加速度分析

电子元件通常通过焊接或插槽方式固定在PCB板上，其加速度的变化可以准确反映PCB板跌落碰撞过程中的实际情况。将PCB板上的电子元件的质量简化为三个质量块，其中顶部和底部集中质量块的加速度曲线如图6所示。可以看出，碰撞过程中底部质量块的加速度增加最快，在1.6ms时达到极限值544.9m／s2，随后加速度逐渐减小，在10ms和13ms时发生二次和三次跌落碰撞，加速度值为269.5m／s2，随后质量块的加速度曲线趋于平缓但带有小幅波动；顶部质量块的加速度在2ms时达到极限值427.3m／s2，与底部质量块的加速度极限值相比减小了21.5%。顶部质量块受到的冲击较小的原因在于包装材料侧板的变形吸收了大量的动能，使得顶部质量块受到缓冲作用。在13ms和18ms出现的加速度峰值分别为392m／s2、211.6m／s2，同样小于底部质量块的加速度峰值，随后加速度曲线趋于平缓波动，这进一步说明了包装材料的变形对能量的吸收作用。

图6 质量块加速度曲线

2.3.3 能量平衡分析

能量平衡图（图5）表明：伪应变能EA与内能EI的比值η＝EA／EI约为1.5%，满足前文理论中提到的EA／EI＜5%的能量平衡要求，分析结果较为准确。

2.4 对比验证

为了进一步研究网格的密度对计算时间和能量平衡以及计算精度的影响，对模型中除刚性板以外的所有部件的网格进行加密处理，总计网格数量为8120，单元类型不变。

根据前文有关稳定时间极限的理论，计算时将设定的稳定时间极限做减半处理，所得结果如图7、图8所示。比较图3、图7可知，网格细化后的应力云图更符合实际情况，应力极值为212.5kPa，较粗网格模型增大5.2%，极值所处的位置并没有发生变化。比较图8、图5可知，网格细化后能量比约为1%，细化网格后的伪应变能显著减小，说明细化网格后所得到的应力结果较粗网格得到的应力结果更准确。细网格、粗网格的CPU计算时间分别为92.4s、716.3s。综合分析单元三维最小尺寸、稳定时间极限、网格数量和运行时间可得表3所示的结果。

图8 细网格能量平衡图

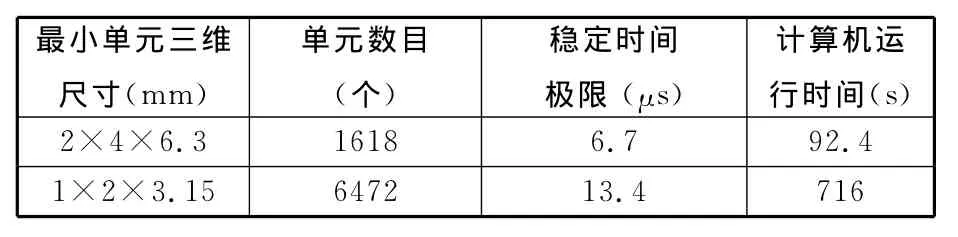
表3 运行时间、稳定时间极限、单元尺寸以及单元数量之间的关系

2.5 实验验证

为验证仿真跌落的准确性，采用加速度传感器测量PCB板实际跌落过程中的加速度数值。由图6可知，PCB板碰撞过程中质量块振荡频率在133～200Hz之间，加速度大小在－490～490m／s2之间，因此选用了ULT2804传感器，该传感器具有静态频率好、灵敏度高等特点，特别适用于低频振动加速度的监测，其量程为±980m／s2，频率为0～800Hz。

分别测量顶部和底部质量块加速度，以确保测量点与跌落过程监测点保持一致。由于碰撞时间极短且加速度数值变化剧烈，故传感器只能监测到PCB板碰撞过程中的加速度极值，其测量值和模拟值对比如表4所示。

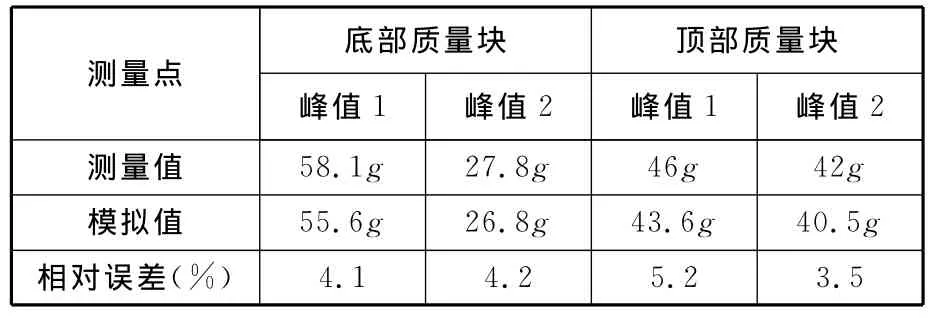
表4 测量值与模拟值对比（加速度）

表4数据表明，测量值与模拟值存在一定误差，且测量值均大于模拟值。引起误差的原因主要包括两点：

（1）PCB板跌落碰撞过程中产生的冲击载荷急剧变化，传感器很难在极短的时间内精确捕捉到加速度极值点。

（2）有限元模型与实际模型存在一定误差，一部分动能储存为网格变形导致的伪应变能，使得模拟值的速度和加速度均小于测量值。

3 结论

（1）ABAQUS／Explicit能够准确地模拟冲击载荷作用下的动态响应，顶部和底部质量块的加速度曲线精确反映了跌落碰撞过程。

（2）进行显式动力学分析时，材料刚度、网格单元的尺寸大小影响计算结果的准确性和稳定时间极限，而总体网格数影响计算机运行时间。

（3）能量平衡理论是显式动力学分析结果精确性的重要环节，本文分析表明：初次分析应采用粗网格以加速收敛，通过验证能量平衡决定是否需要细化网格，以便实现在保证精度的同时缩短计算机运行时间。

（4）线路板跌落分析结果表明，聚苯乙烯包装材料1m高自由落体跌落碰撞时产生的最大应力为226.5kPa，小于 PCB板的跌落安全极限36MPa，满足安全性能要求，并且安全系数较高，可以以此为依据对此包装材料进行轻量化设计，以达到节省材料降低包装成本的目的。

［1］ 屈本宁，张曙红.工程力学［M］.北京：科学出版社，2008.

［2］ 丁剑，李刚，薛澄岐，等.手机塑料外壳地面造型耐撞击性能研究［J］.电子机械工程，2009，25（1）：42－48.

［3］ 王建梅.ABAQUS在电视跌落仿真中的应用［C／DK］.Ds SIMULIA2010中国区用户大会论文集.青岛：达索公司，2010.

［4］ 马映峰，辛志峰.基于ABAQUS分析的计算机系统包装优化设计［C／DK］.Ds SIMULIA2010中国区用户大会论文集.青岛：达索公司，2010.

［5］ 邱杰，彭伟，章巧芳.便携式工具跌落仿真研究［J］.轻工机械，2010，28（5）：42－45.

［6］ 杨永强，李爽，谢礼立.构件跌落碰撞的数值模拟研究［J］.振动与冲击，2010，9（6）：54－58.

［7］ 庄茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析和应用［M］.北京：清华大学出版社，2008.