一种复杂分层介质中电磁探测的正演算法研究

葛勤革 韩逍菲 潘威炎 罗 强

(1.海司信息化部，北京 100036；2.中国电波传播研究所，山东 青岛 266107；3.中国人民解放军91919部队，湖北 黄冈 438000)

引 言

近年来，SLF/ELF频段的电磁波用于地球物理勘探正被广泛重视。在CSEM的正演计算中最早及早期的分析模型都是均匀成层模型，电磁波在这些模型中传播时在接收点处所产生的场值已有解析表达式，并有许多算法可以对这些场值进行快速准确的计算。但是，实际的物理模型不是严格平面分层的，对于这些模型没有解析表达式进行计算。近些年来，随着计算机性能的提高很多人致力于电磁场在不均匀介质中传播的数值算法的研究。

常用的电磁场的数值模拟方法可分为以微分方程为基础的有限差分法、有限元法和以积分方程为基础的积分方程法、矩量法、边界元法两大类。对于我们所讨论的SLF/ELF波的传播问题，由于工作频率很低，实际电磁场的空间变化很快，而时间变化很慢，若采用时域有限差分法则计算过程很难收敛并稳定，误差亦难以控制。若单纯采用积分方程法，对于复杂模型下的计算也面临着矩阵求解以及计算速度方面的一系列问题[1]。对于目前广泛采用的有限元方法，虽然其在解决不均匀结构问题时与其他的方法相比有很大的优越性，但该方法生成网格的成本高，需要进行单元剖分、节点编号等繁重的前处理过程，生成矩阵的存储量大，在实际的计算中这些矩阵往往是病态的，计算的精度和速度都很不理想。

对于探测正演中所涉及的复杂分层结构中电偶极子激发的电磁场的数值计算问题，本文将复杂分层结构看成是均匀分层结构中含有目标体，如果目标体的埋深比较深，并且，导电率与背景介质的导电率反差不大，则可以将均匀分层中的目标体看成对于均匀分层的“扰动”，将仅含均匀分层的初级场与由目标体的“扰动”产生的次级场之和看成含有目标体的不均匀分层介质中的总场。在上述地质条件下，可以忽略目标体内部场的相互作用，避免了积分方程法在方程求解方面所存在的一系列问题。在计算过程中，将充分利用在均匀分层介质电波传播方面的研究成果，结合格林函数的物理意义，对总场值进行直接计算，将该算法称为基于“扰动”的格林函数法。文中给出了该方法在水平电偶源激发，水平n层分层介质中含有目标体时，接收点场强的计算思路。结合水平半空间中含有目标体这一模型分析了该算法的有效性以及需要进一步解决的问题。

1 算法原理

考虑海底N层均匀水平分层背景介质，在最上层沿着x轴方向放置水平电偶极子发射源，接收点设在沿着x轴的一维方向上且位置可变。

当在背景介质的第i层中存在一个目标层时，如图1，可以认为整个区域的电磁场分布将在原来的电磁场分布基础上增加一个“扰动”，即

在这里称背景介质中所对应的场Ein和Hin为初级场，由目标体的“扰动”所产生的场Ese和Hse为次级场，初级场与次级场之和即为接收点处的总场值Etot和Htot.其中，初级场Ein和Hin满足Maxwell方程为

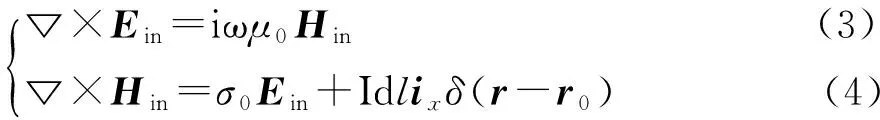
式中：σ0为水平均匀分层介质中的电导率分布；r0是激励源所在的位置。

图1 含有目标体的水平N层分层模型

当存在目标层后，在整个区域内总场分布Etot和Htot应满足

将式(1)～(4)代入(5)、(6)可得整个区域内的次级场满足

(9)

进一步表示为

(14)

3) 目标区域Ω内各个点处所对应的x、y、z三个方向偶极子在接收点处产生的场，即式(14)三阶方阵中各元素的计算。

对于1)、2)两种情况下场强的计算已根据周永祖[3]和葛德彪[4]等人的推导思路进行了具体的推导，并针对本文的算法得到了适合于编程实现的具体表达式，限于篇幅原因将另文发表。对于3)的计算可根据King[5]、潘威炎等人[6-7]给出的积分表达式直接计算。

2 算法验证

选用背景分层介质为最简单的均匀半空间模型，通过在背景介质的区域2中插入目标体Ω的方式来构造不均匀分层结构(如图2左)。这种地质模型下接收点的场强没有解析公式对其进行计算。但是考虑到当接收点离发射源比较近，对于接收点的场强的计算结果应接近于水平无限大四层模型(图2右)下相应接收点场强的计算结果。故下文将通过利用格林函数法计算出的图2左模型的接收点的电场x分量与利用直接积分法计算出的图2右模型的接收点的电场x分量作对比的方式来说明格林函数算法的有效性。

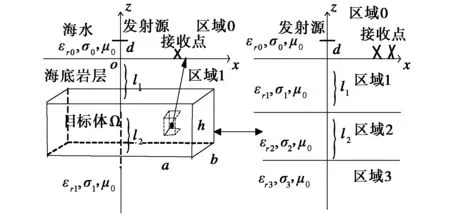
图2 均匀半空间含目标体模型 与水平无限大四层模型

对于图2模型,式(14)矩阵中的格林函数表示为

(15)

(16)

(17)

式(15)、(16)、(17)中的φ′为接收点偏离目标体中第m个剖分单元中心节点的水平相位。将φ′减小π/2可得：Gyx、Gyy、Gyz.

ei(γ1d-γ2z)λ2dλ

(18)

将式(18)中相位φ减小π/2得Gzy.

(19)

式中：J0、J1、J2分别为零阶、一阶和二阶贝塞尔函数。γj=(kj2-λ2)1/2;kj=ω(μ0(ε0εrj+iσj/ω))1/2；j=1，2;对于M、N的具体表达式见参考文献[5]。

取海水的介质参数为：εr0=80，σ0=3.3 s/m；海底岩层：εr1=10，σ1=1 s/m；目标层(四层介质中的区域2)的介质参数：εr2=10，σ2根据需要取值；海底岩层：εr3=10，σ3=1 s/m.各层中的磁导率均为真空中的磁导率μ0.水平偶极子源的工作频率f=1 Hz,距离海底岩层的高度d=10 m.

1) 目标层导电率σ2=0.1 s/m，将图2左模型中目标体的长宽均取为5 000 m，埋深l1取为600 m，采用本文所提算法对于图2左模型中接收点总电场x分量幅值的计算结果与采用直接积分法对于图2右模型中接收点总电场x分量幅值的计算结果对比如图3；将目标层(区域2)的埋深l1设为1 000 m，其他条件不变所得的结果对比见图4所示。

图3 目标体埋深600 m计算结果对比图

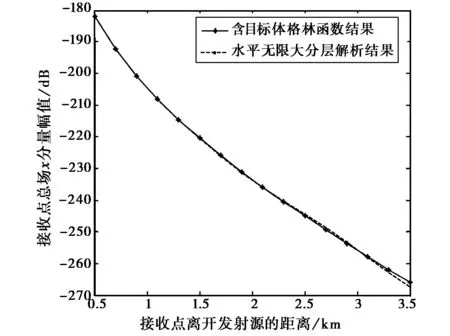
图4 目标体埋深1 000 m计算结果对比图

从图3和图4可以看出：在收发距较小的情况下，计算结果的相对误差均小于10%；当接收点接近或超过目标体的水平边缘时不能再将图2左看作图2右的近似模型，故相对误差也明显增大。另外，通过图3和图4的对比可以看出：当埋深较深时两种算法的相对误差要小的多。这主要是因为对于无限大分层介质，当目标层埋深较深时，由于目标体的存在所产生的侧面波和反射波主要是在远场区起作用，因此，当收发距在埋深的2～3倍范围内，两种模型的近似效果较好，相应的计算误差也较小，收发距小于3 000 m时，相对误差小于10%，从而对算法的有效性进行了初步验证。

2) 从算法的推导过程可以看出：总场中的初级场由背景均匀介质决定，可以认为是已知的。可反映目标体位置及介质特性的是次级场。图5、图6为目标体的长宽均取为5 000 m，埋深1 000 m，导电率取不同的值时接收点处次级电场x分量实部、虚部随发-收距的变化。通过图5、图6可以看出：在目标体所在区域附近，次级场对于总场的作用较强。

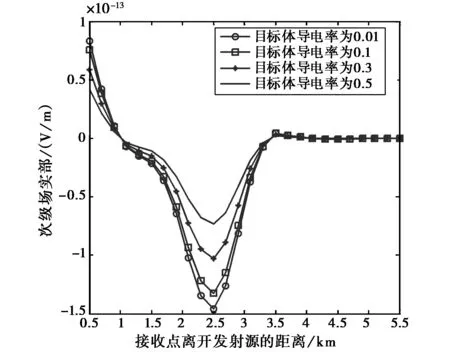
图5 次级电场x分量实部

图6 次级电场x分量虚部

图7为长宽均为5 000 m的目标体位于发射源正下方，垂直埋深1 000 m时次级电场x分量幅值(dB)在xoy面内的分布图。图8为长宽均为1 500 m的目标体，位于发射源正下方左侧500 m，垂直埋深1 000 m时次级场的水平分布图。

通过图7、图8可以看出随着目标体的大小和埋藏位置的不同，次级场的主要作用区域(图中深红色等值线的分布区域)的大小和位置相应地发生了改变，这为反演计算提供了依据。

3 结 论

针对水平分层介质中含有目标体，目标体埋深较深、导电率与背景层的导电率反差不大的地质模型，给出了基于“扰动”的格林函数算法思路，并且选取简单的分层模型对算法的有效性进行了验证。通过验证得出：在该模型下基于“扰动”的格林函数算法对接收点总场进行计算，在避免进行求解积分方程的同时，计算精度可接受。由于采用该算法时主要涉及到含有贝塞尔函数的积分计算，在提高计算速度方面需要进一步研究。

[1] 何展翔, 孙卫斌, 孔繁恕, 等. 海洋电磁法[J]. 石油地球物理, 2006, 41(4): 451-457.

HE Zhanxiang, SUN Weibin, KONG Fanshu, et al. Marine electromagnetic approach[J]. Oil Geophysical Prospecting, 2006, 41(4): 451-457. (in Chinese)

[2] Chen-To-Tai. Dyadic Green Functions in Electromagnetic Theory[M]. 2nd. New York: The IEEE Press, 1993: 55-59.

[3] 周永祖. 非均匀介质中的场与波[M]. 聂在平, 柳清伙, 译. 北京: 电子工业出版社, 1992: 48-61.

[4] 葛德彪. 电磁波理论[M]. 西安: 西安电子科技大学出版社, 1997: 38-48.

[5] KING R W P, OWENS M, WU T T. Lateral Electromagnetic Wave[M]. New York: Springer-verlag Press, 1992: 151-170.

[6] 潘威炎. 长波超长波极长波传播[M]. 成都: 电子科技大学出版社, 2004: 165-170.

[7] 李 凯. 分层介质中的电磁场和电磁波[M]. 杭州: 浙江大学出版社, 2010: 53-72.

[8] WEISS C J, CONSTABLE S. Mapping thin resistors and hydrocarbons with marine EM methods, part II: modeling and analysis in 3D[J]. Geophysics, 2006, 71(6): 321-332.

[9] HE Z X, KURT S, YU G, et al. On reservoir boundary detection with marine CSEM[J]. Applied Geophyiscs, 2008, 5(3): 181-188.

[10] 彭怀云, 陶 伟, 潘威炎, 等. 极低频垂直偶极子在地-电离层中场的数值积分算法[J]. 电波科学学报, 2012, 27(2): 333-338.

PENG Huaiyun, TAO Wei, PAN Weiyan, et al. Numerical integral method for ELF fields excited by vertical electric dipole in asymmetric earth-ionosphere cavity[J]. Chinese Journal of Radio Science, 2012, 27(2): 333-338. (in Chinese)

[11] ZHAO Luanxiao,GENG Jianhua,ZHANG Shengye,et al. 1-D controlled source electromagnetic forward modeling for marine gas hydrates studies[J]. Applied Geophysics,2008,5(2): 121-126.

[12] BADEA E A. Finite-element analysis of controlled source electromagnetic induction using Coulomb gauged potentials[J]. Geophysics, 2001, 66(3): 786-799.