二维物理小波标架去除探地雷达信号随机噪声

石显新 杨秋芬 侯彦威

（1.中煤科工集团西安研究院，陕西 西安 710077；2.西安文理学院物理系，陕西 西安 710065）

引 言

探地雷达（简称GPR）是利用高频无线电波确定介质内部物质分布规律的一种探测方法，近年来在工程与环境等浅层地球物理领域得到广泛应用［1-2］。

在探地雷达技术发展过程中，对接收信号中的噪声处理是一个重要方面［3］。在探地雷达接收信号中存在多种干扰与噪声，因探测目标反射回波信号较弱，甚至可能掩没于干扰与噪声中，直接影响了目标信号的检测与判断，这给数据的处理与解译造成了很大障碍。为获得高精度高分辨率的数据处理与解译结果，需对采集的数据进行预处理，以抑制或去除干扰与噪声，提高数据的质量。

Larsoneur和Morlet［4］首先提出用小波变换去噪的思想，从20世纪90年代开始有大量的将小波变换用于信号去噪的文章发表。朱光明等［5］把小波变换用于一维滤波。Chakraborty和David等［6］对比了短时Foureir变换、连续小波变换（CWT）及匹配追踪算法（MPD）对地震信号作时间-频率域分析的效果，指出MPD优于前两种，且给出了MPD去噪的方法。Miao和 Moon［7］及罗国安等［8］把小波变换用于消除地震记录的面波干扰。章珂等［9］把二进小波变换用于信号的分时分频去噪处理。

在地震资料数据处理中二维物理小波标架的成功应用，是基于地震炮集数据中有效信号（体波）的空间形态是双曲线形状，二维物理小波函数可以很好地与之匹配；而主要的噪声（面波）与体波在空间形态上差异很大。以二维物理小波为母小波，有效信号（体波）在小波域比较稀疏，而噪声（面波）不稀疏，这样在表示体波的有限区域重构信号，就可以衰减面波干扰。将二维物理小波标架用于去除探地雷达信号随机噪声，其原理类似，即探地雷达点目标信号的二维观测数据在空间上也呈双曲线形态，而随机噪声在空间的分布没有规律。若将含有噪声的探地雷达信号变换到二维物理小波域，由于二维物理小波函数与点目标信号能很好地匹配，小波域表示点目标信号的小波系数就比较稀疏，而表示随机噪声的小波系数不稀疏。因此，在表示点目标信号的小波系数区域重构信号，就可以衰减随机噪声。

基于以上认识，作者开展了二维物理小波标架去除探地雷达信号随机噪声的研究，并用二维物理小波标架阈值去噪对两个典型信号进行了去噪处理，证明了该方法的有效性。

1 二维物理小波标架的数学原理

二维小波标架原子具有二维小波的形式［10］。这里使用文献［11］中构造的二维物理小波，其数学表达式为

一维墨西哥帽小波表达式为

在x-t域的双曲线表达式为

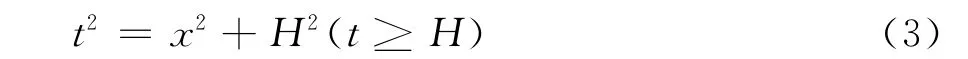
在x方向加上衰减因子e-ax2后物理小波表达式变为

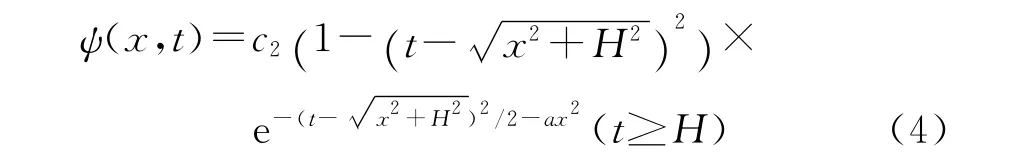
加入衰减因子的目的在于使这种新构造的物理小波满足小波的允许条件。

式（1）、（4）中的a为正实数，反映x方向的衰减；H为双曲线的顶点，可以根据要求设置。

物理小波标架的原子具有以下形式为

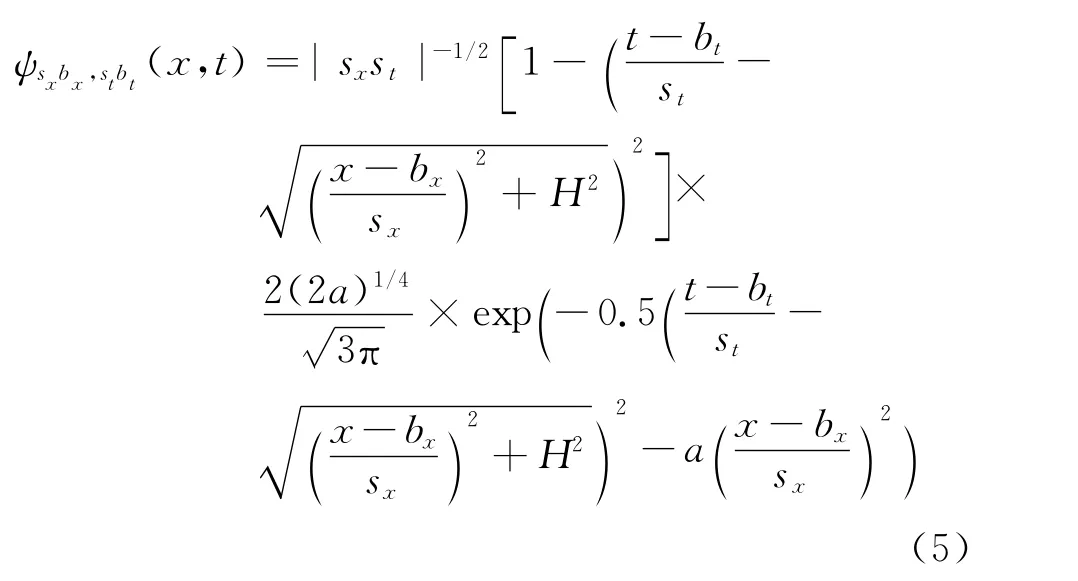
适当的选取时间和偏移两个方向的尺度因子，如

把式（6）中的（b）以式（1）代入后结果为1.证明物理小波适当选取尺度位移因子后构成的二维小波标架，可运用于分解重构二维信号。

小波的尺度因子是局部化分析中改变小波频谱中心和带宽的参量。同一维小波标架对信号的分解重构一样，尺度因子选择应使得各尺度小波频谱对有效信号频谱完全覆盖且尽量覆盖均匀，即各尺度小波的频谱峰值覆盖区域保证错开。这相当于一滤波器组对信号各频带分别滤波。小波满足正交条件时，各尺度的频带完全不重合，重构效果好，而本文中介绍的物理小波不满足正交条件，这就应仔细考察选用的每一组尺度下的小波频带覆盖范围。在具体实现过程中，按二进情况，在频域（f-k），t方向尺度st倍增，频谱在f方向的频带范围压缩为原来的一半；x方向尺度sx倍增，频谱在k方向的频带范围压缩为原来的一半。从用Matlab绘制的各个尺度的物理小波f-k频谱图可以清楚的观察其二维频谱形状、峰值、变化趋势，从而选择合适的尺度范围，更好地对信号进行局部化分析去除噪声，重构有效信号。

当尺度增大到一定程度时，物理小波二维频谱集中在f-k域中心，范围很小，具体实现算法中发现频谱峰值重复覆盖，低频信息多次叠加，表现为k低频分量对重构有效信号干扰大，在x向双曲线信号顶点位置形成一条"直杠"。

通过观察时间及空间尺度变化时二维物理小波在时间-尺度域及频率-波数域的特征，发现二维物理小波函数在频率-波数域呈扇形分布，这时二维物理小波具有最高的频率及波数分辨率。小波函数在时间方向上明显变宽，也就是说时间分辨率变低，频带变窄。小波函数在空间方向上明显变宽，即空间分辨率变低，也就是波数域展布变窄。

2 二维物理小波标架去噪的实现

2.1 物理小波标架去噪的实现

实现物理小波标架去噪的步骤如下:

1）人工合成点目标探地雷达数据。为了逐步验证效果，分别制作了理想的无噪数据及含有色噪声污染的数据。2）实现数据的物理小波标架分解，得到每一组时间-偏移尺度下的分解系数。3）通过实验选取阈值，实现小波域阈值去噪。4）从处理后的小波域系数重构有用信号，完成去噪。

2.2 信号分解和重构公式及实现方法

在进行信号分解时，需要固定两个尺度因子，计算如下的二重积分

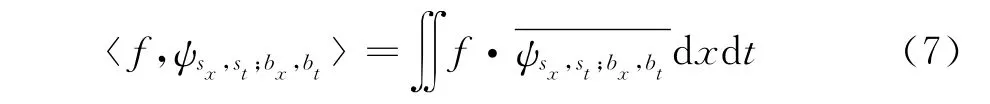
分别对信号f（x，t）和物理小波ψ（x、t）沿两个方向采样，x、t方向采样分别为M、N点，构成M×N阶的矩阵，当x、t单位都归一化后，就不必考虑两个方向采样的差异，视为采样间隔均为1，这样便可以按数字信号来实现。分解公式变为

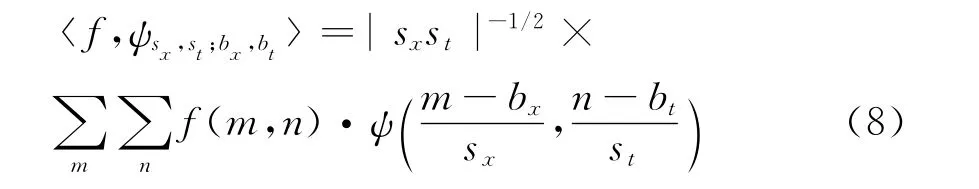
按照小波变换信息的冗余性及实际应用中的要求，选取尺度因子的一些离散值。按照常用的二进小波变换的方法，令

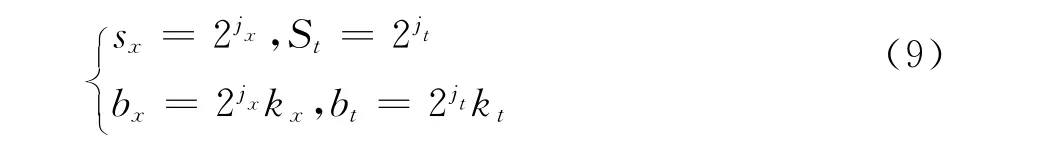
分别固定两个尺度因子，小波域系数不抽取时，式（8）相当于计算一个二维相关函数:

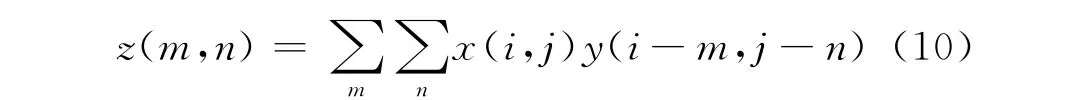
令y′=y（-m，-n），则二维相关函数计算化为二维卷积:

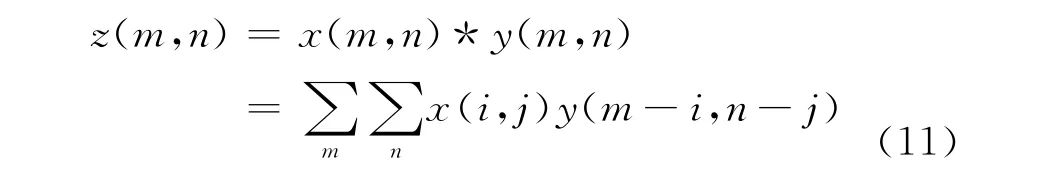
利用二维离散傅里叶变换（DFT）及逆变换（IDFT）的性质，可以通过频域计算卷积

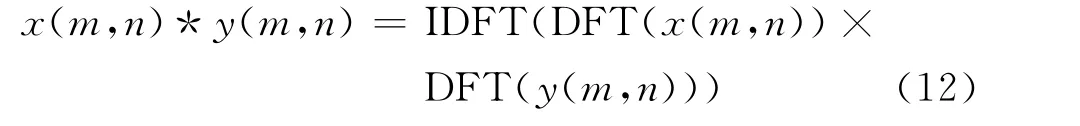
式（12）中DFT和IDFT可由二维快速傅里叶正、逆变换FFT2和IFFT2实现。

重构信号时，要满足紧标架重构公式:

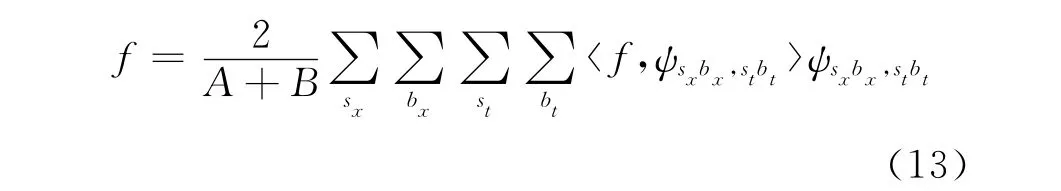
记WTsx，st（bx，bt）为一组尺度下的二维小波域系数矩阵，式（13）离散后变为

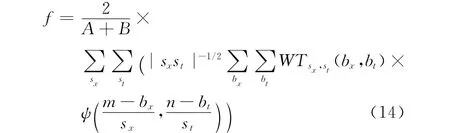
可分别对式（14）进行二维卷积，重构每一组尺度下的二维信号，再累加，最后就能得到重构信号。

2.3 信号分解重构举例

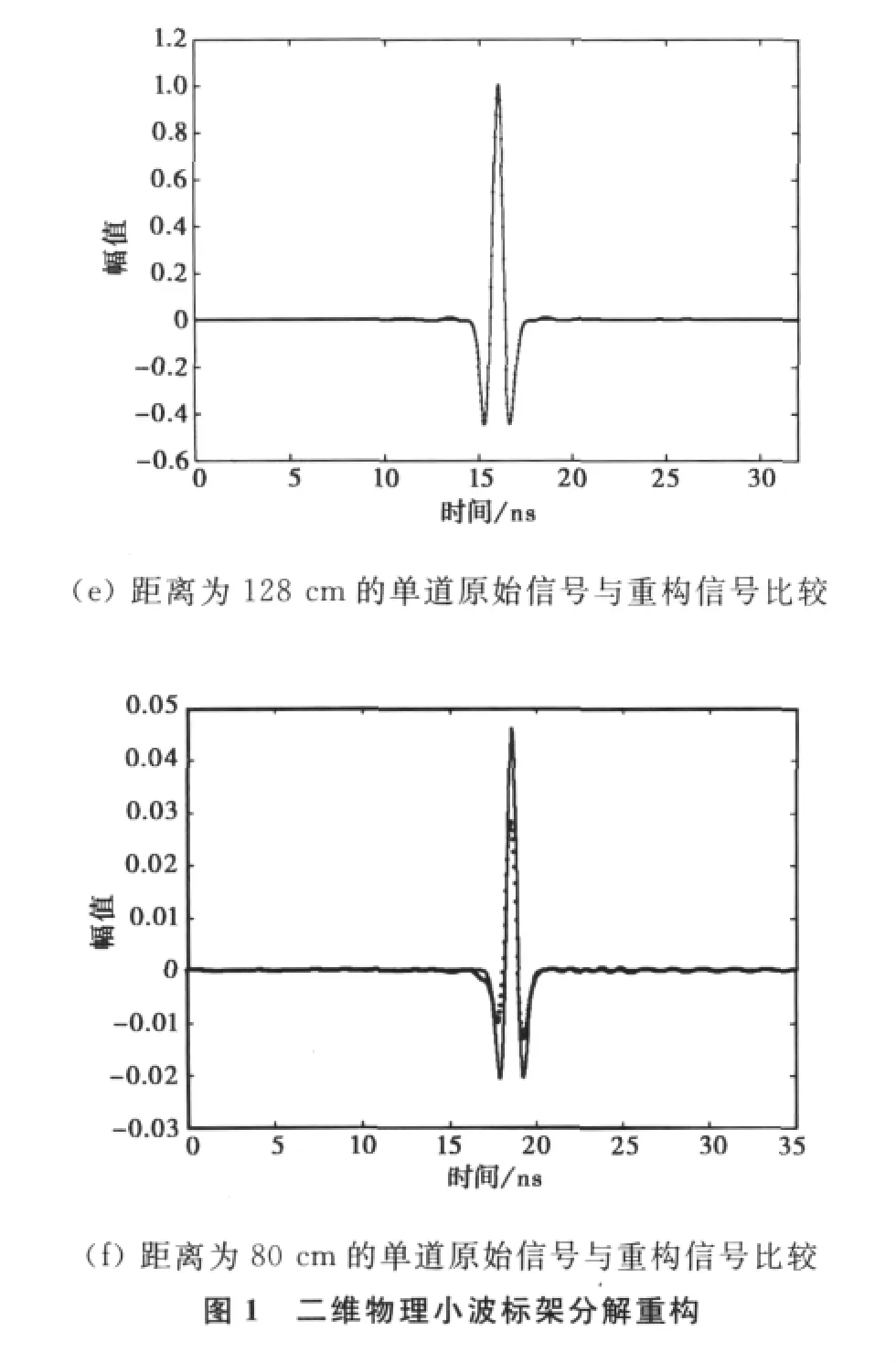
图1（a）为一探地雷达点目标模拟散射信号，其中空间方向256个采样点，采样间隔1 cm，时间方向1024个采样点，共40ns.可以看出，反射信号有较明显的双曲形态。每一道信号的反射子波为Ricker子波，其主频为800MHz.图1（b）、（c）是利用式（8）对图1（a）作小波分解后由式（14）重构的结果。比较两图，可以看出基本上重构了信号。

图1（e）与图1（f）是不同距离时的单道原始信号与重构信号的对比，细实线代表原始信号，点划线代表重构信号。信号的边界重构不完全，这与一维标架类似，因为二维物理小波不构成紧标架，信号重构存在误差。但在实际信号处理中这些误差是可以接受的。

2.4 小波域阈值去噪的实现

小波域阈值去噪方法的原理是:分别在各个尺度下选取去噪的阈值 ，然后对小波域系数按以下规则处理:

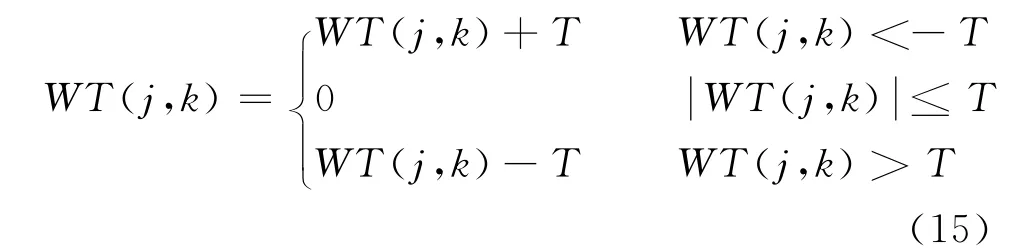
物理小波标架去噪的关键是当数据投影到物理小波标架上时，信息是冗余的，双曲线形状的有效信号的二维频谱与某个尺度的物理小波标架原子二维频谱相似，故可以映射出绝对值较大的系数。因二维频谱重合区域相关度小，使得有色噪声映射的系数较小，去噪效果较好。具体实现中，可以分别从每组尺度下小波域系数中挑选典型的道，确定该组尺度应选取的阈值，从而达到压制噪声的目的。

根据式（3）、（9）及小波标架的算法，结合小波域阈值去噪的原理，就可以实现二维物理小波域阈值去噪。

3 模型算例

图2为一探地雷达点目标模拟散射信号，其中空间方向256个采样点，采样间隔1cm，时间方向1024个采样点，共40ns.可以看出，反射信号有十分明显的双曲线形态。每一道信号的反射子波为Ricker子波，主频800MHz.需要说明的是，图2与图1（a）都是点目标散射模拟信号，但模拟时参数选择不同，图2的双曲线形态更为明显。

图2 理想模拟信号

3.1 信噪比1∶1

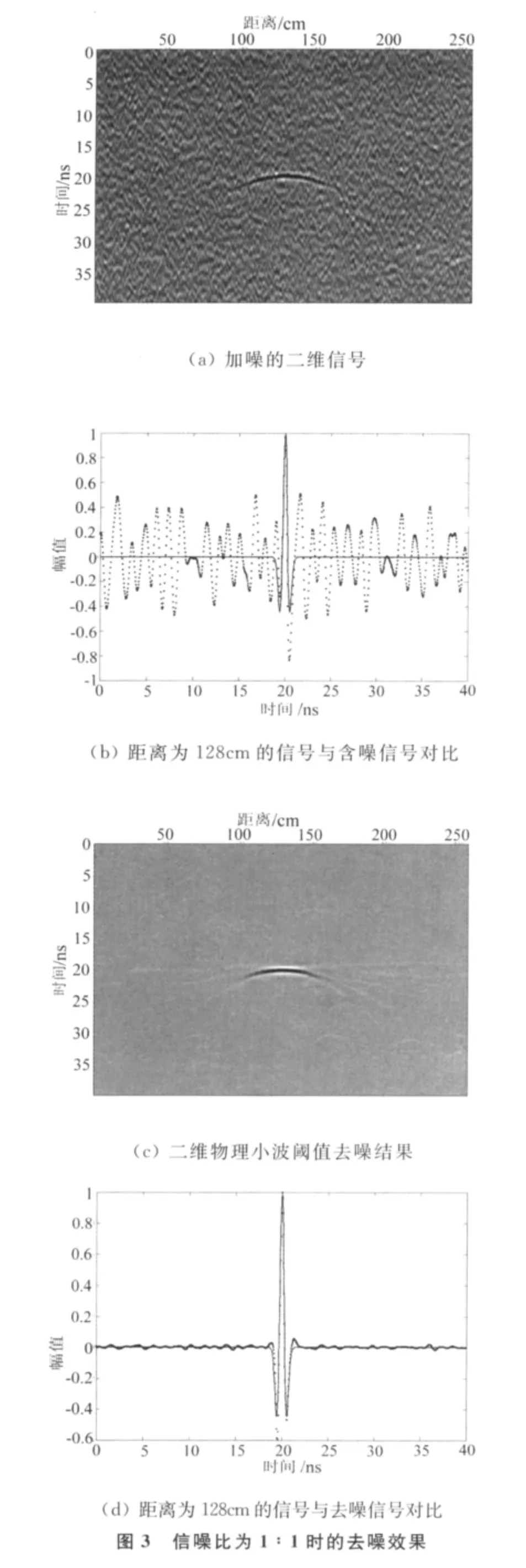
在图2的基础上加上噪声，其中信号与噪声最大幅值比为1∶1，如图3（a）所示，信号受到了较大影响，由于相关性，仍能看到信号的基本形态。为了更清楚地看到噪声对信号的影响程度，从图3（a）中抽取距离为128cm处的一维信号与原始无噪信号重叠显示，如图3（b）所示，其中点划线为含噪声信号，细实线为原始信号，可以看出，从一维信号中无法分辨有效信号的位置及形态。另外，因为所加噪声与有效信号同频带，所以传统的一维滤波不能去除噪声。图3（c）是对图3（a）阈值去噪结果，可以看出:噪声受到了很好的压制，同时信号也受到了一定的影响，但点目标的反射形态仍然比较清晰。图3（d）为从图3（c）中抽取距离为128cm处的一维信号与原始无噪信号重叠显示，其中点划线为去噪信号，细实线为原始信号，也可以看出，噪声受到了较好的压制。

3.2 信噪比1:3

与图3（a）相比，图4（a）中信号与噪声最大幅值比为1∶3，信号已完全淹没于噪声中。从图4（a）中抽取距离为128cm处的一维信号与原始无噪信号重叠显示，如图4（b）所示，其中点划线为含噪声信号，细实线为原始信号，噪声明显大于信号。图4（c）是对图4（a）阈值去噪结果，可以看出:噪声受到了较大的压制，点目标的反射形态比较清晰。图4（d）为从图4（c）中抽取距离为128cm处的一维信号与原始无噪信号重叠显示，其中点划线为去噪信号，细实线为原始信号，可以看出，信号的基本形态得到了恢复。与图4（c）相比，虽然效果要差一些，但这是在信噪比很低，一般认为是废弃资料的情况下，取得这样的处理结果，也说明了该方法的有效性。

图4 信噪比为1∶3时的去噪效果

4 结 论

综上所述，利用二维物理小波函数模拟与探地雷达点目标散射信号匹配的小波函数，对含噪声的探地雷达模拟信号进行小波域阈值去噪，在信噪比较低的情况下仍能取得较好的效果，证明了该方法的有效性。

［1］陈文超，师振盛，汪文秉，等.小波变换在去除探地雷达信号直达波的应用［J］.电波科学学报，2000，15（3）:352-357.CHEN Wenchao，SHI Zhensheng，WANG Wenbing，et al.Suppressing the direct wave noise in GPR data using the 2-D continue directional wavelets［J］.Chinese Joural of Radio Science，2000，15（3）:352-357.（in Chinese）

［2］郭 晨，刘 策，张安学.探地雷达超宽带背腔蝶形天线设计与实现［J］.电波科学学报，2010，25（2）:221-226.GUO Chen，LIU Ce，ZHANG Anxue.Design and implement of an UWB bowtie antenna with backcovity for ground penetrating radar［J］.Chinese Journal of Radio Science，2010，25（2）:221-226.（in Chinese）

［3］周辉林，田 茂，熊俊志.探地雷达回波信号的特征提取和分类［J］.电波科学学报，2006，21（4）:586-589.ZHOU Huilin，TIAN Mao，XIONG Junzhi.Feature extraction and classification of ground penetrating radar echo signals［J］.Chinese Journal of Radio Science，2006，21（4）:586-589.（in Chinese）

［4］LARSONNEUR J L，MORLET J.Wavelets and seismic interpretation［C］／／ Wavelets，Time-Frequency Methods and Phase Space，1st Int Wavelets Conf Marseille，December 14-18，1989:126-141.

［5］朱光明，高静怀，王玉贵.小波变换及其在一维滤波中的应用［J］.石油物探，1993，32（1）:1-10.ZHU Guangming，GAO Jinghuai，WANG Yugui.Wavelet transform and its application to 1-D filtering［J］.Geophysical Prospecting for Petrole，1993，32（1）:1-10.（in Chinese）

［6］CHAKRABORTY A.Application of wavelet transform to seismic data［C］／／64th SEG Meeting American.Los Angeles，October 23-28，1994:725-728.

［7］MIAO X G.Application of the wavelet transform in seismic data processing［C］／／62th SEG meeting A-merican，1994:1461-1464.

［8］罗国安，杜世通.小波变换及信号重建在压制面波中的应用［J］.石油地球物理勘探，1996，31（3）:338-349.LUO Guoan，DU Shitong.Application of wavelet transform and signal reconstruction in surface wave elimination［J］.Oil Geophysical Prospecting，1996，31（3）:338-349.（in Chinese）

［9］章 珂，刘贵忠.二进小波变换的地震信号分时分频去噪处理［J］.地球物理学报，1996，39（2）:265-270.ZHANG Ke，LIU Guizhong，ZOU Dawen，et al.Seismic data time-frequency domain denosing based on dyadic wavelet transform［J］.Chinese Journal of Geophysics，1996，39（2）:265-270.（in Chinese）

［10］ZHANG Rongfeng，ULTYCH T J.Physical wavelet frame denoising［J］.Goephysics，2003，68（1）:225-231.

［11］杨秋芬，石显新.探地雷达信号直达波的去除［J］.煤炭学报，2008，33（7）:770-774.YANG Qiufen，SHI Xianxin.Removing for the direct wave noise in ground penetrating radar［J］.Journal of China Coal Society，2008，33（7）:770-774.（in Chinese）