星载Ku波段波导缝隙天线的缝隙特性分析

王宏建 刘世华，2 郝齐焱，2 易 敏 陈 雪 刘 广

（1.中国科学院空间科学与应用研究中心微波遥感技术重点实验室，北京 100190；2.中国科学院研究生院，北京 100049）

引 言

波导缝隙阵列天线以其结构紧凑、重量轻、增益高、副瓣低、口径利用率高、口径场分布易于控制等优点，广泛应用于雷达、通信等领域。通常缝隙阵列的设计可分为三个步骤［1］:① 按天线电性能要求，确定波导尺寸、面阵元数、各缝上的电压；② 结合缝隙特性曲线，考虑各个缝间互耦，由Elliott设计方程调整缝隙长度及偏置量；③ 重复步骤②直到阵中缝处于谐振状态并满足所要求的电压分布。关于缝隙特性的描述，已有众多的学者采用不同的方法［2］研究过，近年时域有限差分（FDTD）等技术［3-4］也被用来精确描述缝隙特性。

商业电磁软件以其快速、高效率的特点，被越来越多地用于波导缝隙天线的设计中。以基于有限元法的高频电磁仿真软件Ansoft HFSS为例，齐美清等［5］采用它得到开缝波导的散射参数，提取了辐射缝隙的自导纳和有源导纳，有效地提高了缝隙天线的设计效率；金剑等［6］利用HFSS的S参数仿真结果，采用等效网络法对互耦环境下缝隙的导纳参数进行了计算；赵怀成等［7］采用数值逼近法直接计算阵列中的缝隙归一化导纳，然后用HFSS验证了设计方法的正确性；还有人用HFSS的参数扫描及优化功能设计了波导窄边缝隙阵天线［8-9］，并通过试验样机作了验证。而Elliott提出的有源导纳法为波导裂缝阵天线的辐射阵面设计提供了理论基础，该方法考虑了辐射缝隙间互耦的影响［10］和波导内部高次模的影响［11］，可用于包括电介质填充的波导等阵列天线的设计［12］。

在星载Ku波段缝隙阵列天线设计中，由于电性能要求和结构空间限制，选定半高的非标准波导。考虑到半高波导中更容易产生高次模影响的特点，以及设计的成本和效率问题，文章将HFSS与Fortran编程相结合应用于该类天线的设计。在对HFSS进行准确性验证的基础上，通过HFSS仿真分析缝隙模型，获得了辐射缝隙和耦合缝隙的特性。然后结合Elliott提出的设计方程，用Fortran编程计算了8×10波导缝隙阵列天线的缝隙参数，并用HFSS优化天线阵整体结构参数，最后加工了8×10波导缝隙阵列天线。测试结果与仿真结果基本吻合，均满足要求，良好的测试结果验证了用HFSS获取缝隙特性曲线的正确性及设计方法的有效性。

1 理论分析

1.1 非标准波导中的缝隙特性分析

采用谐振式波导缝隙阵列天线，每个缝隙的中心间距取λg／2（λg代表波导波长），为了实现高效率，分支波导终端短路，形成驻波阵。各个缝隙的理想工作状态是谐振，其长度参数均在λ0／2（λ0代表自由空间波长）左右。在实际工作前，特别针对WR90型标准波导，研究了f0=9.375GHz时的缝隙特性，将HFSS仿真结果与Stegen［13］及L.G.Josefsson［14］的实测结果进行了比较，良好的结果验证了HFSS在该类应用中的准确性。

1.1.1 宽边纵向辐射缝隙

宽边纵向辐射缝隙模型如图1所示，缝隙的电参数包括:缝隙宽度w，缝隙高度t，缝隙长度lr，缝隙中心偏离波导中心线的距离x.综合考虑到加工难度、天线工作带宽及微放电等因素，在设计初已分析并确定了缝隙宽度w和高度t的具体值。该段波导用空气填充，总长为3λg／4，距离缝隙中心λg／4处是波导的终端短路板，另一端距离缝隙中心λg／2处是激励波端口。

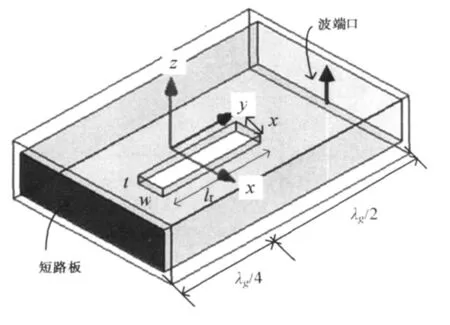
图1 宽边纵向辐射缝隙模型

图2 缝隙谐振长度与偏置的关系

在波端口处的Y参数可以等效为距端口λg／2处的缝隙中心的Y参数，根据波导缝隙的基本设计理论［2］，在谐振时纵向缝隙的导纳为实数，即Im（Y）=0.给定缝隙偏置，通过计算不同缝隙长度下的参数ActiveY（有源导纳），可分析出缝隙的谐振长度，再结合波阻抗Z0，就可计算出不同偏置下谐振时的归一化输入电导。图2是缝隙谐振长度与偏置的关系曲线，实线表示缝隙终端为矩形头时的变化关系，虚线表示缝隙终端为圆形头时的变化关系，分析结果发现二者在数值上近似为平移关系，在最后加工天线时，可根据该结果把矩形头辐射缝隙修正为圆形头缝隙。另外，与文献［3，13］中的结果相比，图2中曲线变化更陡一些，这是由于半高非标准波导的高度小，更容易激励起高次模，缝隙的谐振长度对其偏置变化更加敏感。缝隙谐振长度与偏置的关系可表示为［15］

图3是缝隙的归一化谐振电导与偏置的关系，将HFSS仿真结果与Stevenson经典公式［2］的计算结果进行比较，在偏置较小时，二者吻合较好，随着偏置的增大，二者逐渐偏离，因为Stevenson的公式在缝隙偏置为0时的情况下结果准确，偏置越大，误差就会越大［15］。缝隙归一化谐振电导与偏置的关系［15］表示为

在缝隙阵列中，由于辐射缝隙之间的互耦存在，如果使用单个缝隙谐振长度时的值，缝隙的有源阻抗并不是纯实数，这就涉及到缝隙长度在非谐振时的导纳。Stegen［13］在对波导宽边纵向缝隙的研究中发现，以缝隙电导和电纳与谐振电导之比为纵坐标，缝隙长度与谐振长度之比为横坐标，在缝隙不同偏置条件下得到的归一化曲线形状十分相似。为了获得半高非标准波导中缝隙的Stegen曲线，在不同偏置下，结合图2结果，对0.9lr≤l≤1.1lr范围内的缝隙长度进行计算，得到其有源导纳并归一化处理，结果如图4所示，左右纵轴分别是归一化电导和归一化电纳，这里归一化对象是缝隙的谐振电导，而图3的归一化对象是波导的波阻抗。图中拟合曲线由不同偏置下的结果取平均得到。该曲线可用函数［15］h和变量y 表示为

图3 缝隙归一化谐振电导与偏置的关系

式中:横坐标y=l／lr，表示缝隙长度和谐振缝隙长度之比；实部h1（y）=G（x，y）／Gr（x，y=1）；虚部h2（y）=B（x，y）／Gr（x，y=1）.

图4 缝隙归一化导纳与归一化长度的关系

1.1.2 中心倾斜耦合缝隙

宽边中心倾斜耦合缝隙模型如图5所示，包括两个长度均为λg的正交矩形波导，中间由耦合缝隙相连接，该模型将波导壁厚度近邻为零，只取波导内腔结构，有益于节省计算时间。耦合缝隙的电参数包括:缝隙宽度w，缝隙高度t，缝隙长度lr，缝隙长度方向中心线偏离波导中心线的角度θ.用HFSS分析时，两根波导共四个端口均设定为激励端口，以实现终端阻抗匹配。

图5 宽边中心倾斜耦合缝隙模型

S.R.Rengarajan定义耦合缝隙的谐振条件［16-17］为缝隙处前向散射波与入射TE10波反相，该条件等同于［3］:在频率和倾角一定时，以缝隙长度为变量，谐振时耦合波导向分支波导耦合的能量最大。在图5模型中，可以通过传输参数S31和S41［3］来判断耦合能量的多少。在45°≤θ≤90°范围内的传输参数与0°≤θ≤45°内的传输参数幅度相同，相位相反［18］，因此对0°到45°内的缝隙特性作分析即可。图6、图7分别是谐振长度和传输参数S31、S41、S11与倾斜角的关系。

图6 谐振长度随倾斜角的变化曲线

从图6可见，耦合缝隙谐振长度随倾斜角的变化很小，由于是半高非标准波导，与文献［13］中的标准波导相比，该曲线相对陡一些。图7中，随着倾斜角的增大，从端口1耦合到端口3、4的能量逐渐增多，在θ=45°时最大，实际耦合波导中，多个耦合缝隙以λg／2为间距排列，传输参数还会受缝隙间的互耦影响。

图7 传输参数随倾斜角的变化曲线

1.2 波导缝隙阵列设计

Elliott提出的平面缝隙阵列设计方程［8-10］为

式中:Yna为单个缝隙的有源导纳；Vns为缝隙电压；Vn为模式电压；gmn为第m 个和第n个缝隙间的互耦电导计算公式［9］。该设计方法考虑了外部缝隙间的互耦影响。在应用中，第一设计方程写为

第二个设计方程，考虑了波导内部高次模的影响，特别有益于非标准波导中的缝隙阵设计。分母中第一项是自谐振分量，第二项为外耦合分量，要满足各缝隙的有源导纳谐振，即为纯实数，应该满足

还有输入导纳匹配方程，由于采用了波导中心耦合馈电，归一化有源导纳之和为2，即

根据Elliott设计方程（4）～（8）和缝隙特性曲线（图2～4、6、7），通过Fortran编程，设计了波导馈电的8×10平面缝隙阵列。该阵列天线包括3部分:辐射阵面（由若干条分支波导组成）、与分支波导交叉放置的耦合波导、为耦合波导馈电的馈电网络。该阵列天线的辐射阵面分成四个区，用四条耦合波导耦合馈电，通过1～4等幅同相波导功分网络对耦合波导馈电。天线实物如图8所示。

图8 8×10天线实物图

2 仿真及实际测试

用HFSS仿真了8×10阵列天线的电性能。方向图如图9所示，E面和H面的副瓣电平分别是-24.2dB和-29.2dB；主波束有良好的对称性，3 dB波束宽度为10.9°.驻波如图10所示，中心频点处的驻波为1.04，由于设计中采用了频带展宽措施，中心频率附近的驻波曲线变化平坦，1.3以下带宽为420MHz，具有较宽的频带特性。

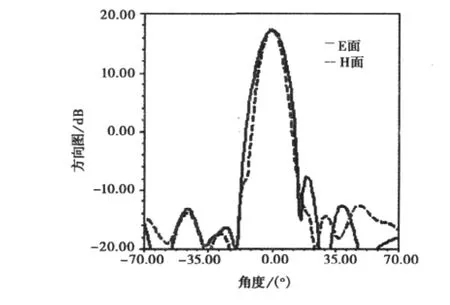
图9 8×10阵列天线方向图仿真结果

在中科院空间科学与应用研究中心的天线近场测试系统中完成了电性能测试。方向图如图11所示，E面和H面副瓣电平分别是-29dB和-27.5 dB，与仿真结果相比，E面实测副瓣电平较好，H面实测副瓣电平提升了1.2dB；主波束对称性较好，3 dB波束宽度为10°.驻波如图12所示，中心频点处的驻波为1.1，驻波在1.3以下的带宽为340MHz，与仿真结果相比，中心频率处的驻波高了0.06，1.3以下的驻波带宽比仿真结果少了80MHz.

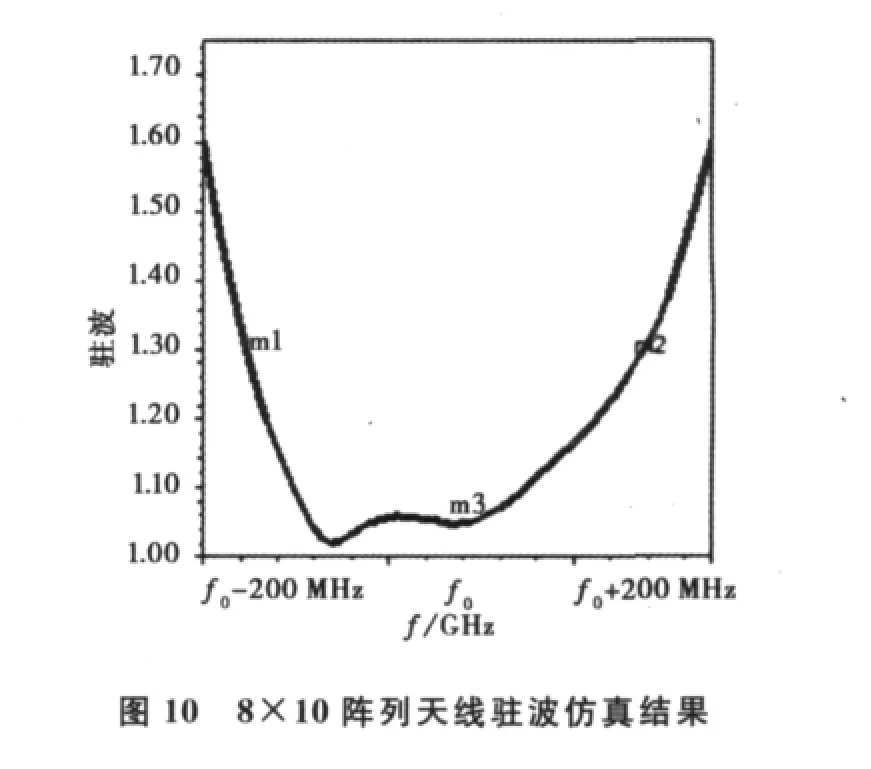
副瓣电平、驻波、波束宽度等的实测结果与仿真结果有偏差，主要是加工误差和测试误差的影响所致。谐振阵列工作在中心频率时，理论上缝隙的有源导纳是实数，天线的口径场相位面为同相。当工作频率变化时，产生以下效应:缝隙的有源导纳特性产生变化；驻波峰值位置偏离缝隙中心；缝隙间距偏离λg／2；缝隙终端所接的λg／4长的短路板，在工作频率变化时产生一定的电纳；缝隙间的互耦发生变化。而加工误差会引起中心频率的偏移，受以上诸因素影响，天线的匹配条件变坏，口径场的幅度、相位分布变坏，天线的副瓣电平抬高、增益下降，也会提高天线的输入驻波比。

整体上实测结果与仿真结果基本一致，均满足设计指标要求。

3 结 论

结合天线实际需求将HFSS与Fortran编程相结合用于星载Ku波段波导缝隙阵。通过HFSS给出了半高非标准波导中的宽边辐射缝隙和耦合缝隙的特性曲线，结合Elliott提出的平面缝隙阵设计方程，考虑了辐射缝隙间互耦因素及波导内部高次模影响，用Fortran编程计算了8×10波导缝隙阵列天线的缝隙参数。天线近场测试结果表明:天线副瓣电平、驻波、主波束宽度等和仿真结果基本一致，均满足设计指标。与工程使用的实验法比较，这种方法克服了传统方法中为了减少试验件加工工作量带来的误差、节约了设计成本、提高了工作效率，同时还考虑了非标准波导易产生高次模影响的特点。良好的测试结果验证了用HFSS获取缝隙特性曲线的正确性及设计方法的有效性，可用于后期大型阵列的设计。

［1］王宏建，高本庆，刘瑞祥，等.遗传算法在波导裂缝阵列天线设计中的应用［J］.电子学报，2002，30（3）:309-312.WANG Hongjian，GAO Benqing，LIU Ruixiang，et al.The application of genetic algorithms（gas）on the design of the waveguide slotted array［J］.Acta Electronica Sinica，2002，30（3）:309-312.（in Chinese）

［2］林昌禄，聂在平.天线工程手册［M］.北京:电子工业出版社，2002:273-298.

［3］WU Ren，GAO Benqing.Full wave analysis of broad wall slot's characteristics in rectangular waveguides［J］.IEEE Transactions on Antennas and Propagation，2004，52（9）:2436-2444.

［4］丁晓磊，王 建，林昌禄.耦合纵缝馈电的短路波导宽边纵缝阵的分析与设计［J］.电波科学学报，2001，17（4）:422-426.DING Xiaolei，WANG Jian，LIN Changlu.The analysis and synthesis of a longitudinal slot-fed array in a broad wall of a shorted waveguide［J］.Chinese Journal of Radio Science，2001，17（4）:422-426.（in Chinese）

［5］齐美清，汪 伟，金谋平.基于HFSS的波导裂缝有源导纳的计算方法［J］.雷达科学与技术，2006，4（2）:121-124.QI Meiqing，WANG Wei，JIN Mouping.Computation method for active admittance of waveguide slot based on HFSS［J］.Radar Science and Technology，2006，4（2）:121-124.（in Chinese）

［6］金 剑，万笑梅，汪 伟，等.波导平板裂缝天线阵的设计［J］.雷达科学与技术，2007，5（3）:232-235.JIN Jian，WAN Xiaomei，WANG Wei，et al.Design of plannar waveguide slotted antenna arrays［J］.Radar Science and Technology，2007，5（3）:232-235.（in Chinese）

［7］赵怀成，吴 文，汤一铭，等.小型波导缝隙天线阵的改进设计方法研究［J］.电波科学学报，2007，22（6）:1025-1028.ZHAO Huai cheng，WU Wen，TANG Yi ming，et al.Improvement of design method for small rectangular waveguide slot arrays［J］.Chinese Journal of Radio Science，2007，22（6）:1025-1028.

［8］武 伟，路志勇.波导窄边缝隙阵列天线的分析与设计［J］.无线电工程，2009，39（1）:42-44.WU Wei，LU Zhiyong.Analysis and design of edge slot waveguide array antennas［J］.Radio Engineering of China，2009，39（1）:42-44.（in Chinese）

［9］李知新，任 朗.矩形波导窄边缝隙分析方法述评［J］.电波科学学报，1999，14（2）:235-241.LI Zhixin，REN Lang.Review of analysis method of the inclined slots on the narrow wall of a rectangular waveguide［J］.Chinese Journal of Radio Science，1999，14（2）:235-241.（in Chinese）

［10］ELLIOTT R S，KURTZ L A.The design of small slot arrays［J］.IEEE Transactions on Antennas and Propagation，1978，26（2）:214-219.

［11］ELLIOTT R S，O'LOUGHLIN W R.The design of slot arrays including internal mutual coupling［J］.IEEE Transactions on Antennas and Propagation，1986，34（9）:1149-1154.

［12］Elliott R S.An improved design procedure for small slot arrays of shunt slots［J］.IEEE Transactions on Antennas and Propagation，1983，31（1）:48-53.

［13］JASIK H.Antenna Engineering Handbook［M］.2nd ed.New York:McGraw-Hill，1989.

［14］JOSEFSSON L G.Analysis of longitudinal slots in rectangular waveguides［J］.IEEE Transactions on Antennas and Propagation，1987，35（12）:1351-1357.

［15］ELLIOTT R S.Antenna Theory and Design［M］.Englewood Cliffs，NJ:Prentice-Hall，1981:408-411.

［16］RENGARAJAN S R.Characteristics of a longitudinal／transverse coupling slot in crossed rectangular waveguides［J］.IEEE Microwave Theory and Techniques Society，1989，37（8）:1171-1177.

［17］RENGARAJAN S R.Compound coupling slots for arbitrary excitation of waveguide-fed planar slot arrays［J］.IEEE Microwave Theory and Techniques Society，1990，38（2）:276-280.

［18］RENGARAJAN S R.Analysis of a centered-inclined waveguide slot coupler［J］.IEEE Microwave Theory and Techniques Society，1989，37（5）:884-889.