能 量 拍 脉 动 与 波 粒 二 象 性

□田瑞生

( 中北大学理学院，山西 太原 030051)

相对论理论与量子理论并称为近代物理的两大支柱，在此基础上物理学发展迅速，并取得了辉煌的成就；但是两个理论所对应微观物理图象的不协调也是物理学界一直有争论的问题。

一、自由粒子能量的拍脉动

爱因斯坦在解释光电效应时引入了光子的概念，并给出了光子的能量E=hν。对于质量为m0的实物粒子，相对论理论给出其静止时的能量E0=m0c2。本文认为所谓能量则不应该是静止的，而应该是活跃的。如果把能量理解为单位时间内物质的活跃度，那么实物粒子的能量就可以类比于光子能量的形式给出。德布罗意曾把实物粒子的能量表示成如下形式1)：

E0=m0c2=hf (1)

本文认为光子能量中出现的频率是光的波动频率，如果认为能量有脉动，则脉动频率应该是波频的两倍。对于质量为m0的粒子，其能量脉动频率应满足如下关系：

其中h为普朗克常数，f0为粒子能量的脉动频率。当粒子运动时，其能量为E=mc2，相应的脉动频率f满足：

粒子运动时的脉动频率要高于粒子静止时的脉动频率(运动时间延缓)。如果具体考虑粒子运动时能量的脉动，由于运动时快脉动的主体是一个慢脉动，因此会产生拍脉动现象。相应的拍脉动频率fp满足：

Ek为粒子的动能。当粒子以速度v在空间运动时，其拍脉动峰值的空间间距为：

二、德布罗意波长与薛定谔方程

当粒子在空间运动时，其能量会形成拍脉动，时空形态如同波传播。对(5)式取经典近似，可得到脉动波的空间波长为：

P为粒子的动量，λ便是粒子德布罗意波长。由此本文认为所谓波粒二象性应该理解为：其粒子性是指粒子的不弥散；其波动性是指能量的时空行为呈现拍脉动特性。

引入一个波函数：

ψ(x,t)=ei(px-Ekt)/h(7)

其中P为粒子的动量，Ek为粒子的动能。此函数的[Reψ(x,t)]2能完好地描述自由粒子能量的拍脉动，因此就将此函数对应于一个自由粒子。

对于非自由粒子，如果其能量的拍脉动被一个实函数的平方描述，则对于此函数可进行如下展开2)：

此处E为粒子的经典能量。对(8)式作如下运算：

势场V的变化通过改变粒子的动能而影响粒子能量的拍脉动，相应地会改变波函数的相速度，但不会改变德布罗意波长的对应关系，也就是说将(11)给出的关系应用于波的描述将不会改变能量脉动波的描述原则，因此联立考虑(9)、(10)、(11)式便可得到薛定谔方程：

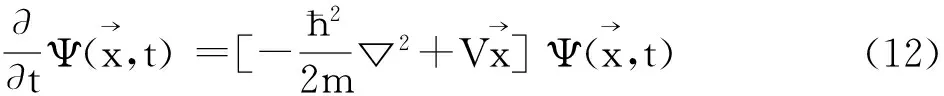
三、波函数与微观图象

量子理论给出的波函数是以概率波的图象描述粒子质量的时空分布；本文给出的波函数是以能量脉动波的图象描述粒子能量的时空分布。由于质量与能量具有确切的关系，因此两种图象给出的波函数是同一个波函数。对于归一化问题，概率波要求对质量归一；能量脉动波要求对能量归一，因此在归一化问题上也是一致的。

当粒子处于定态时，要求波函数给出的分布不随时间变，由此便可得到微观系统的量子化。这样对波函数的理解应当扩展：它不仅是对能量脉动的描述，同时反过来会制约其描述对象。

本文脉动波的图象承认粒子的轨道概念，但是因为有能量脉动，因此其轨道绝不是经典意义下的轨道，而是能量拍脉动的轨道。

粒子的时空特性被波函数描述，行进中遇到双缝时，波函数经双缝后其行进方向将呈现干涉性概率状分布，因此有双缝干涉。

粒子遇到势垒时，由于粒子能量拍脉动，因此是否穿过势垒将呈现概率特性。当势垒高于粒子动能而穿过便是隧道效应；当势垒低于粒子动能而将粒子挡回便是粒子能量脉动的表现。

对于量子力学的不确定关系，如果把不确定关系理解成测不准关系，则与本文给出的微观图象不矛盾。

四、高速粒子

当粒子高速运动时，总能量的脉动频率与静止能量的脉动频率差异大，拍现象消失。此时能量的脉动仍然是快脉动与慢脉动的叠加，可看作是运动能量的脉动与静止能量的脉动的组合性叠加，相应的波函数应满足K-G方程。如果考虑相对论时空效应以及粒子自旋对能量脉动的影响，波函数应满足狄喇克方程。

五、问题

本文观点成立的前提是微观粒子能量的脉动，当然也涵盖质量的脉动。微观测量给出的不确定性结果我们总是把它理解为概率波的原因。如果设计一个实验能排除概率波的原因，比如让电子通过一个狭小的电场(或磁场)形态可调的区域而测到了与概率波不确定性给出的结果不相同的结果，则本文观点成立。

六、结语

量子理论的成就辉煌，但其波粒二象性的物理图象是只可意会却难以言表。如果本文观点成立，则可给出可以言表的波粒二象性的物理图象。如果我们没有概率波的观念，当我们见到一维谐振子的波函数时，相信更多的人会认为那是能量在振动。

参考文献：

[1]Olenick R P，Apostol T M，Goodstein D L. Beyond the Mechsanical Uviyverse[M].London: Cambridge University Press. 1986.

[2]曾谨言.量子力学[M].北京：科学出版社,1982.