高频地波雷达稀疏频率波形优化设计

胡 恒 贺亚鹏 庄珊娜 朱晓华

(南京理工大学电子工程与光电技术学院 南京 210094)

1 引言

工作于高频段(3～30 MHz)的高频地波雷达(High Frequency Surface Wave Radar, HFSWR)利用垂直极化电磁波沿海面传播损耗小的特点，可探测视距外的舰船及低空突防的飞机、导弹等目标，且作用距离可达300～400 km，能有效覆盖常规微波雷达和天波超视距雷达的监视和引导“盲区”，在军事和民用领域得到了广泛应用[1−3]。然而来自广播电台、民用电台及近海工作的无线通讯系统的强功率同频窄带干扰，严重影响了HFSWR系统的目标探测性能。如何根据外界频谱环境，实时高效地抑制窄带干扰已成为HFSWR系统亟待解决的重要课题[4,5]。

自20世纪90年代以来，针对窄带干扰在雷达系统中的抑制问题，国内外研究人员提出了一系列的处理方法。一种比较直接的方法是采用零陷滤波器[6]，即接收滤波器在干扰所在频带内形成零陷，降低干扰对信号处理系统的影响，但该方法抑制干扰的同时也造成了目标回波能量的损失，且会引起匹配滤波器(Matched Filter, MF)失配问题，导致弱小目标无法检测。针对该问题，文献[7,8]创造性地选取不连续的雷达工作频段合成大带宽来满足高分辨力及抗干扰要求，解决了零陷滤波器能量损失及MF失配问题。依据这一思路，文献[9]提出了基于稀疏频率的最优干扰抑制发射和接收波形设计方法，通过优化设计频域稀疏的发射波形，可充分利用不连续的频谱而不被其他干扰所影响；然而最优干扰抑制稀疏频率波形具有旁瓣高的缺陷，虽然通过加窗能够在一定程度上缓解高旁瓣带来的多目标分辨问题，但该方法会引起失配信噪比损失及主瓣展宽，造成邻近目标分辨力下降，影响HFSWR系统检测性能。文献[10,11]在设计稀疏频率波形时则综合考虑了功率谱和自相关函数性能，解决了由于MF失配造成的信噪比损失及主瓣展宽问题，然而其波形设计目标函数仅对功率谱阻带进行了约束，未考虑通带性能，而实际雷达工作环境中不存在完全没有干扰的频带，因此其设计的波形不能与干扰环境充分匹配，限制了信干噪比(Signal to Interference and Noise Ratio, SINR)的进一步提高。

本文基于稀疏频率波形设计的思想，提出了一种新的波形优化设计目标函数，该函数不仅能够灵活地根据外界环境对HFSWR发射波形的通带和阻带性能进行约束，而且在优化发射波形的功率谱密度(Power Spectrum Density, PSD)的同时对积分旁瓣电平(Integrated Sidelobe Level, ISL)也进行约束，并能够根据实际应用要求灵活均衡二者优化权重。然后提出了一种循环相位共轭梯度求解方法，以较快的收敛速度得到最优相位调制波形。优化波形能够有效抑制同频窄带干扰且旁瓣较低，同时避免了失配处理造成的信噪比损失及主瓣展宽问题，具有较强的战场环境适应能力，仿真结果验证了其有效性。

2 目标函数建立

设HFSWR基带发射波形经离散化采样后表示为

其中N为序列长度，T表示转置，则发射波形的频谱为

其中Ts为采样间隔。在存在窄带干扰的情况下，为抑制外界干扰，提高接收信号的SINR，获得更大的信息容量，希望在干扰频带内发射波形的能量尽可能小，同时在非干扰频带内能量可均匀地分布或集中在某些频带内，即根据不同频带干扰功率的大小分配不同的信号发射功率[12]。本文通过对频带加权实现信号发射功率的优化分配。假设发射波形在频带[fL,fH]内分布，其功率谱具有Ns个阻带，其中第k个阻带的频带范围为 [fs1,k,fs2,k]，针对不同的阻带干扰严重程度的不同，设计波形时对每个阻带分别加权，权重为ws,k；同时功率谱具有Np个通带，其中第k个通带的频率范围为，同样地，对不同的通带也可分别加权，权重为wp,k，由此定义发射波功率谱约束的目标函数为

其中H表示共轭转置，矩阵R和C的第m行第n列元素分别为

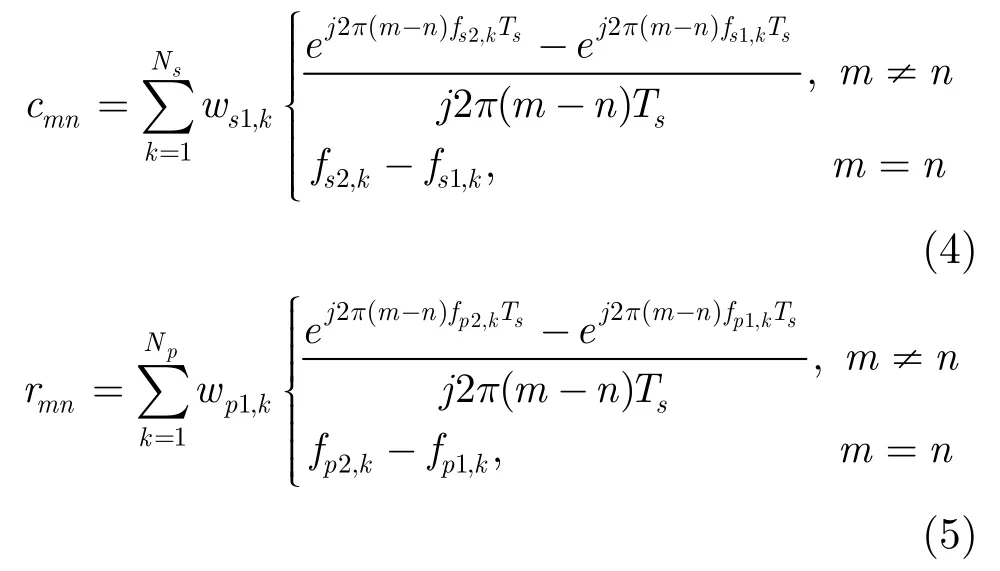
仅对式(3)进行优化得到的发射波形具有优异的干扰抑制性能，但旁瓣较高，在多目标场景中会导致大目标旁瓣掩盖小目标的主瓣，严重影响HFSWR的检测性能。在实际雷达系统设计中，抑制干扰的同时还希望发射波形自相关函数能够有足够低的旁瓣。目前优化旁瓣的准则主要有两种：峰值旁瓣电平(Peak Sidelobe Level, PSL)和ISL。以PSL为准则优化波形的旁瓣电平将会随着波形长度的增加而增大，而ISL优化准则通过降低整体旁瓣电平，减小峰值积分旁瓣电平比(Peak Integrated Sidelobe level Ratio, PISR)，较为稳定[13]。因此，本文采用ISL来衡量发射波形的旁瓣性能。优化波形s的ISL定义为

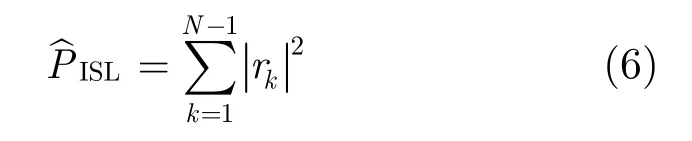
其中rk为发射波形的自相关函数，即

注意到PISL是s的四次函数，在迭代过程中会严重影响优化算法的收敛速度，根据文献[14]中的讨论，ISL的极小化问题可等效为式(8)二次函数的极小化问题：

4）目前高校多采用放录像的形式让学生进行相应的实验学习，学生只能初步了解实验内容。这种实验方式应用在控制工程基础教学中，对培养本科生应用能力和工程实践能力是极为不利的，与国家要求的本科素质培养也有一定的差距。

为了在抑制干扰的同时优化发射波形的旁瓣，即使得PPSD和PISL均取得最小。该问题为典型的多目标优化问题，解决该问题有多种解法，本文采用经典的加权系数法进行求解。构造联合优化PPSD和PISL性能的目标函数为

其中l为PPSD和PISL的折中加权因子，反映了其重要程度。当l取0或1时，目标函数P退化为对PPSD或PISL的独立优化求解问题。将式(3)和式(8)代入式(9)，得

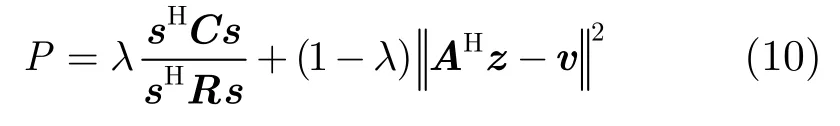
3 波形联合目标函数优化求解

式(10)所示的波形优化目标函数P是典型的多变量非线性函数。目前，求解该类目标函数的方法主要有交替牛顿迭代法、循环共轭梯度法、模拟退火法(SA)，粒子群优化法(PSO)等。其中PSO早期收敛速度较快，但到了寻优的后期，其收敛速度迅速减慢，且容易收敛到局部极小。SA通过模拟物理力学系统在降低系统内能时状态变迁这一物理过程实现对复杂多变量目标函数的优化求解，收敛结果与初始值选取无关，较好地解决了寻优时陷入局部解的问题，但收敛速度较慢。交替牛顿迭代法计算过程中需要存储和计算Hesse矩阵并求逆，算法复杂度较高。循环共轭梯度法仅需利用一阶导数信息，不需要矩阵存储，且具有较快的收敛速度和二次终止性等优点，在实际应用中得到了广泛应用。

为充分利用发射机的发射功率，避免放大器非线性对发射波形的影响及昂贵放大器的使用，实际应用中发射波形多采用恒模信号(Constant Modulus Sequences, CMS)[11,14,15]，因此选取 CMS的作为优化目标波形并提出一种快速的循环相位共轭梯度法优化求解目标函数。算法通过对目标函数P中s和v两个未知变量进行交替迭代优化，并在计算s最优值时引入了相位共轭梯度算法，达到快速收敛的目的。

根据上述分析，当s固定时，容易得到，v与同向时P取得最小值，即

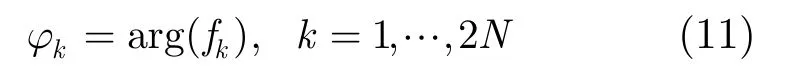
其中

当v固定时，使得P取最小值的s无解析解，需要采用优化数值方法求解，又由于使用CMS作为优化目标波形，因此采用收敛速度较快的相位共轭梯度法对其求解。

相位共轭梯度优化算法最核心的部分是求解目标函数P的梯度，但由于P的前半部分为分数形式，直接求其梯度较为复杂，因此通过求取其Taylor级数的方法间接求解梯度，令

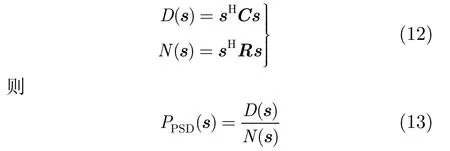
定义相位扰动矩阵为

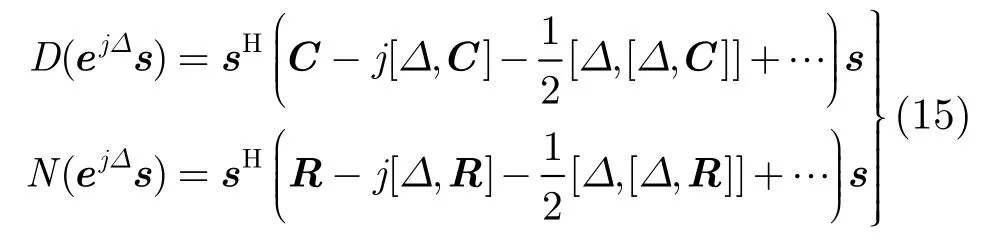
其中[·,·]为李代数乘积，定义为[A,B] =AB−BA，将D(ejDs)根据倒数函数的级数展开，得

由式(15)和式(16)，得到PPSD(s)关于扰动D的一阶微分为

其中Im表示取向量的虚部，Diag(A)表示矩阵A的对角元所形成的列向量。

则目标函数P的梯度可表示为

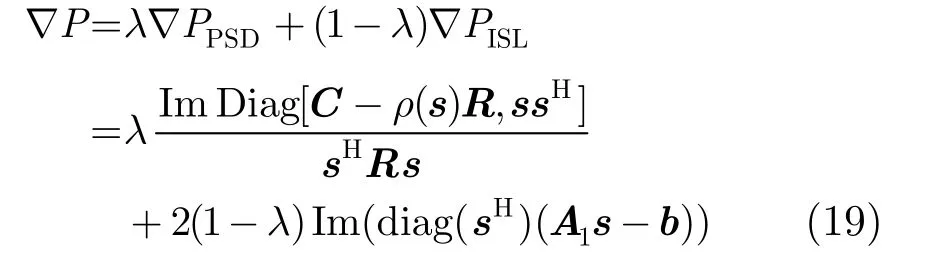
根据式(11)和式(19)，则采用循环相位共轭梯度算法优化求解基于积分旁瓣约束的HFSWR稀疏频率波形步骤如下：

步骤 1 设i=0，任意选取s的初始值s0，根据HFSWR实际应用环境适当选取l，设置迭代终止阈值e。

步骤 2 根据式(11)求解v0，式(19)求解搜索方向

步骤 7i=i+ 1，循环迭代步骤3至步骤5，直到优化波形满足终止条件。

4 仿真结果及分析

为验证本文算法有效性，假设HFSWR工作在4.11～4.82 MHz波段，根据文献[16]测试结果，该频带内有6个可用频带，分别为(单位：MHz)4.11～4.14,4.26～4.27, 4.29～4.31, 4.37～4.39, 4.46～4.48,4.51～4.82。设采样频率fs= 7 10 kHz，波形时宽T=400 μs，因此波形的采样点数。下文分别从旁瓣抑制能力，不同l对最优波形设计的影响，算法收敛速度和优化波形在存在干扰环境下实际处理效果4个方面对本文提出的HFSWR波形优化算法进行数值仿真，以验证其有效性和优越性。为方便进行比较，实验1到实验3的阻带权重ws,k和通带权重wp,k均取为1，实验4的阻带权重ws,k设为1，通带权重wp,k取为带内干扰功率的倒数，干扰功率分别为[0.2,0.8,0.1,0.9,0.4,0.7]。

实验 1旁瓣抑制能力。根据上述假设条件，采用本文算法和文献[9]中提出算法优化波形的PSD和自相关函数(AutoCorrelation Function, ACF)性能如图1所示。经过数值计算得到，两种算法优化波形的的PISR分别为1.34 dB和-1.87 dB，通带平均功率比阻带平均功率分别高出 22.7 dB和 23.2 dB。可看出在得到近似的 PSD性能时，本文提出算法具有更好的旁瓣抑制能力，提高了HFSWR的检测性能。

实验 2不同l对最优波形设计的影响。为验证选取不同l值对HFSWR优化波形的影响，图2分别将l=0.5和l=0.9优化波形的 PSD和 ACF性能进行对比。其中l=0.5时PISR为4.79 dB，优于l=0.9时的1.34 dB，但通带平均功率比阻带平均功率只高出 12.3 dB，小于l=0.9时的 22.7 dB，这是由于l取值越大，对PPSD的权重越大，优化波形具有更优的PSD，即优化结果的PSD性能越好；反之，l取值越小，对PISL的权重越大，优化波形具有更优的ISL，即优化结果的ISL性能越好。通过实验，这一结论得到了验证。调整l的取值，可以灵活地改变设计波形的PSD和ACF性能，但一种性能的提高是以其他性能的下降为代价的，发射波形ISL的降低会影响波形的PSD性能，使其不能与环境完全匹配，带来一定的信噪比损失。在实际应用中，应根据实际情况配置l的大小，以满足具体环境和任务要求。

实验 3算法收敛速度对比。为验证本文提出算法在优化HFSWR发射波形收敛速度快的特点，将本文算法，文献[9]中算法及文献[10]中采用的PSO算法在计算发射波形过程中式(10)的收敛情况绘于图3中。其中PSO算法参数选取同文献[10]：群体规模为100，惯性权重为1，加速常数为2。从图3中可以看出，本文算法在20次迭代后就可收敛至最优结果，文献[9]中算法在50次迭代后逼近最优结果，而PSO算法在迭代早期收敛速度很快，但后期收敛速度迅速减慢，容易收敛到局部最优。

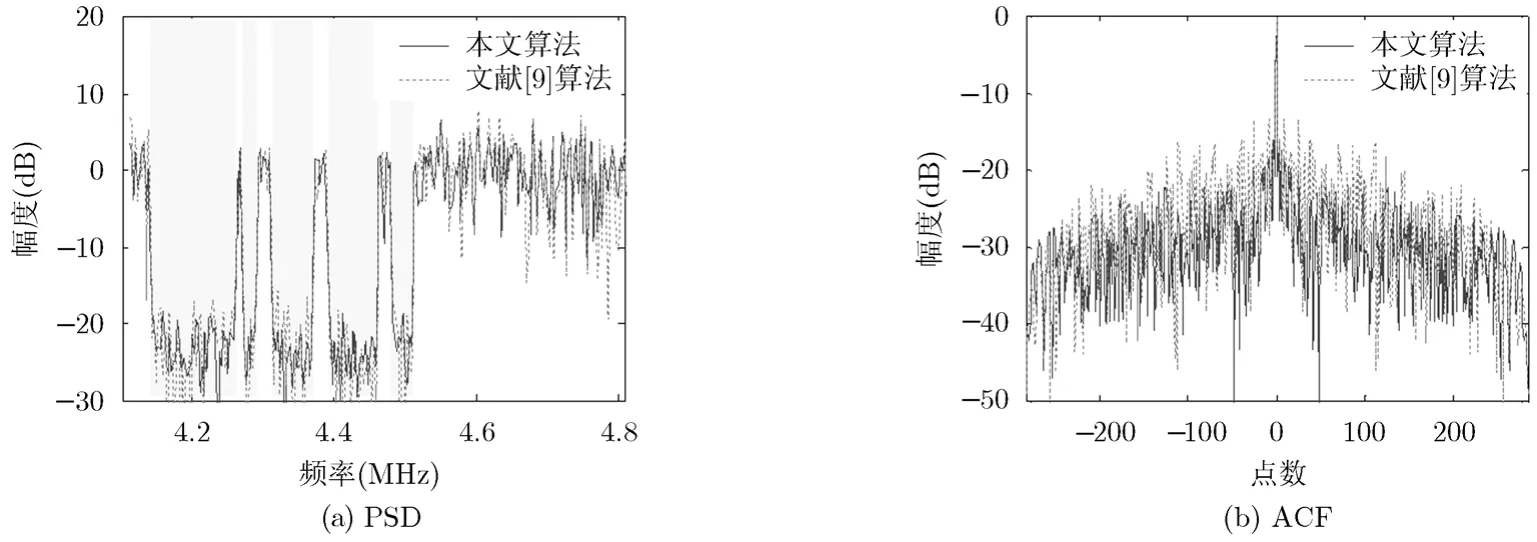
图1 l=0.9时PSD和ACF性能

图2 l=0.5和l=0.9时PSD和ACF性能

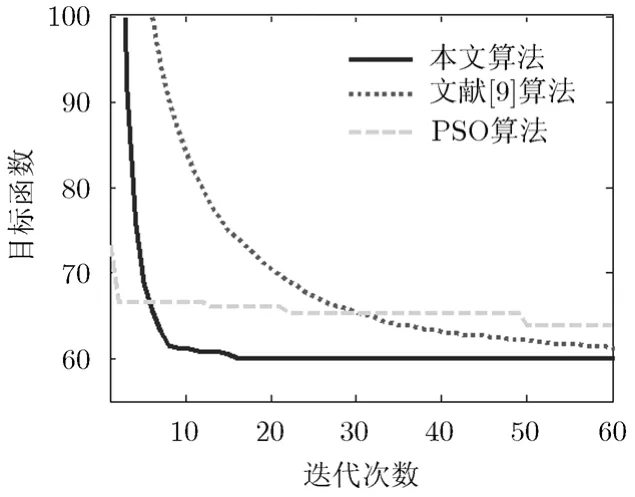
图3 不同算法目标函数随迭代次数的变化

实验 4干扰环境下优化波形多目标MF输出对比。为验证本文设计波形对干扰抑制的实际效果，将窄带干扰引入回波，对比线性调频信号(LFM)，随机相位编码信号(RPC)，文献[9]，文献[10]，文献[11]算法优化波形和本文算法优化波形 MF输出结果。假设在第[10,30,70]个距离门内存在3个目标，RCS分别为[1,4,1.5]，回波的SINR为-20 dB，各信号脉冲压缩输出结果如图4所示，图中虚线位置处为目标真实所在位置。可以看出，LFM和RPC由于没有针对窄带干扰进行抑制，仅能分辨出RCS大的目标，RCS较小的目标完全被干扰淹没，无法检测。文献[9]算法优化波形虽能在一定程度上抑制窄带干扰，但其旁瓣较高，无法检测出大目标附近的小目标。文献[10]和文献[11]算法优化波形虽综合考虑了功率谱和自相关函数性能，但由于只考虑对阻带加权而未对环境中通带进行匹配，影响了 SINR的进一步提高，且文献[10]中的PSO算法易收敛到局部最优，严重影响优化效果。而本文提出算法能够针对外界干扰，对各个通带和阻带分别加权，并能够均衡优化PSD和ACF性能，在抑制干扰的基础上还能很好地控制发射波形的 ISL，脉冲压缩后仍然能够较好地检测目标。

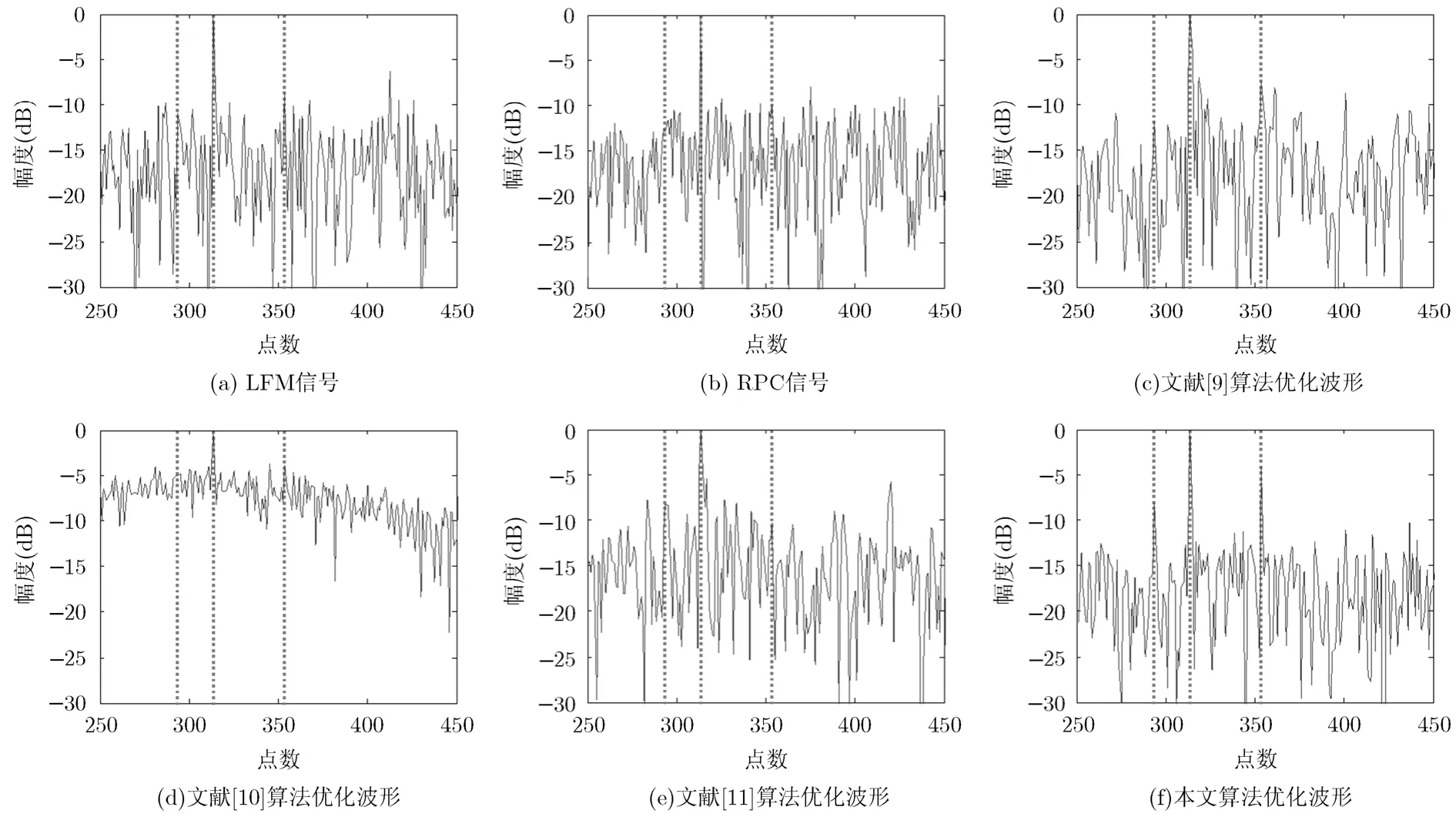
图4 存在干扰时不同信号脉冲压缩输出结果

5 结论

利用频域稀疏波形抑制窄带干扰以提高日益复杂的雷达战场适用能力是一种新思路，且发射波形的自相关函数对雷达检测性能也至关重要。本文提出的波形优化设计算法能够在 PSD性能优势损失较小的前提下明显改善波形的ACF性能，并能够根据实际战场环境灵活优化平衡二者关系。随后提出的循环相位共轭梯度算法具有收敛速度快，运算量较小的特点，仅需很少的迭代次数即可得到最优恒模相位编码波形，适合实际工程应用。与传统雷达采用的线性调频，随机相位编码信号相比，优化波形具有更优良的多目标检测性能。

[1] Grosdidier S, Baussard A, and Khenchaf A. HFSW radar model: simulation and measurement [J].IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(9): 3539-3549.

[2] Gupta A and Fickenscher T. Correlation based novel detection scheme for HF surface wave radar [C]. Microwave Conference, Darmstadt, Germany, March 14-16, 2011: 1-4.

[3] Maresca S, Greco M, Gini F,et al.. The HF surface wave radar WERA Part II: spectral analysis of recorded data [C].2010 IEEE International Radar Conference, Washington, DC,USA, May 10-14, 2010: 969-974.

[4] Guo X, Sun H B, and Yeo T S. Interference cancellation for high-frequency surface wave radar [J].IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(7): 1879-1891.

[5] Wang W and Wyatt L R. Radio frequency interference cancellation for sea-state remote sensing by high-frequency radar[J].IET Radar,Sonar&Navigation, 2011, 5(4):405-415.

[6] Song T L, Musicki D, and Sol D K. Target tracking with target state dependent detection [J].IEEE Transactions on Signal Processing, 2011, 59(3): 1063-1074.

[7] Green S D and Kingsley S P. Improving the range/time sidelobes of large bandwidth discontinuous spectra HF radar waveforms[C]. Seventh International Conference on HF Radio Systems and Techniques, Nottingham, UK, July 7-10, 1997:246-250.

[8] Kutuzov V M. Synthesis of non-regular multitone signals and algorithms of their processing[C]. International Conference on Signal Processing, Beijing, China, October 14-18, 1996:813-816.

[9] Lindenfeld M J. Sparse frequency transmit-and-receive waveform design[J].IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3): 851-861.

[10] Wang G H and Lu Y L. Sparse frequency transmit waveform design with soft power constraint by using PSO algorithm [C].2008 IEEE International Radar Conference, Rome, Italy,May 26-30, 2008: 1-4.

[11] Wang G H and Lu Y L. Designing single/multiple sparse frequency waveforms with sidelobe constraint [J].IET Radar,Sonar&Navigation, 2011, 5(1): 32-38.

[12] Zhang W S and Yang L Q. Communications-inspired sensing:a case study on waveform design [J].IEEE Transactions on Signal Processing, 2010, 58(2): 792-803.

[13] Deng H. Polyphase code design for orthogonal netted radar systems[J].IEEE Transactions on Signal Processing, 2004,52(11): 3126-3135.

[14] Stoica P, He H, and Li J. New algorithms for designing unimodular sequences with good correlation properties[J].IEEE Transactions on Signal Processing, 2009, 57(4):1415-1425.

[15] Pillai S U, Li K Y, Zheng R C,et al.. Design of unimodular sequences using generalized receivers[C]. 2010 IEEE International Radar Conference, Washington DC, USA, May 10-14, 2010: 729-734.

[16] Leong H W and Dawe B. Channel availability for east coast high frequency surface wave radar systems[R]. Defence Research Establishment Ottawa, November 2001.