一种基于高维频率拟合技术的恒虚警穿墙雷达目标定位算法
丁一鹏 吴世有 王 伟 方广有
①(中国科学院电子学研究所 北京 100190)
②(中国科学院研究生院 北京 100049)
1 引言
通过微波信号检测并追踪隐藏在墙、门等不透明障碍物后的人体目标是近年发展起来的一项新兴技术,在军事和民用领域都存在着广泛的应用前景[1,2]。其中,连续波穿墙雷达凭借其低廉的价格、简单的结构以及优秀的静态杂波抑制等诸多优势一直受到人们的广泛关注[3]。然而相关研究发现,当检测的不同目标间具有足够接近,甚至重叠的多普勒频率,以至不同目标无法从频域得到准确识别时,连续波穿墙雷达的检测性能将出现大幅的降低,即发生频率模糊现象[4,5]。因此,如何在频率模糊区域内准确识别、定位目标一直是连续波穿墙雷达的研究热点。此外,由于穿墙探测环境往往具有复杂多变的特点,在不同检测条件下,甚至相同条件不同检测时段内,雷达回波中所包含的杂波分量可能存在较大差异。为了保证雷达在不同环境下的检测概率,传统定位算法通常会选取一个较低的固定噪声门限,以保证有用的目标调制信号不受损失。因此,在某些低信噪比时刻,处理信号中的残留噪声分量将导致虚假目标的产生。这不仅影响了系统的检测精度,还可能对最终定位结果的可读性和可靠性造成较大影响。
针对以上问题,本文提出了一种基于高维频率拟合技术的恒虚警目标定位算法。该算法首先根据恒虚警检测技术实时调节系统的噪声阈值,抑制虚假目标的产生,然后利用2维拟合处理实现不同目标分量的初步识别和参数估计,最后结合检测的实际需求,通过自适应频率拟合算法对分离的各分量进行高维度的参数修正,并给出目标准确的定位结果。实验结果证明该算法能有效去除检测过程中的虚假目标,在不增加硬件复杂度的前提下,提高系统对不同探测环境的适应能力,并能在频率模糊区域内准确识别和定位多个目标,为连续波穿墙雷达的高精度定位提供可能。
2 经典连续波穿墙雷达定位算法
2.1 基于短时傅里叶分析的定位算法
基于短时傅里叶分析的传统定位算法通过目标间相异的多普勒频率识别不同目标,并利用其相应的相位信息完成对目标的定位[6]。其主要计算为
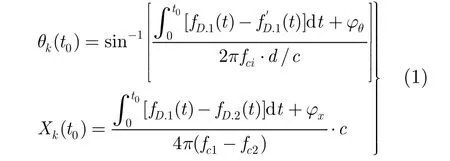
研究发现,在通常情况下,基于短时傅里叶分析的定位算法具有计算量小和理论直观的优势,然而当检测的不同目标间具有足够接近甚至重叠的多普勒频率时,该算法的性能将大幅降低。这种现象被称为频率模糊效应,并成为连续波雷达的主要缺陷之一[6,7]。
为了克服频率模糊问题,文献[8]提出了一套基于多普勒和阵列处理的联合算法。该算法通过引入阵列加权,将雷达的回波信号投影到“频率-波达方位-距离”3维平面,然后从多个维度联合识别不同目标并完成各目标的定位,具有较高的检测精度和抗混淆能力。然而,该算法检测性能的提升是以牺牲雷达的硬件指标为代价的。为了达到令人满意的检测效果,该算法采用阵列接收,其检测性能的提升与使用接收单元和载波频率的个数成正比。这不仅增加了雷达的尺寸、重量及成本,还可能带来诸如信道串扰,高功耗等一系列问题,实际应用中存在着较大的局限性[9]。
2.2 基于2维频率拟合技术的定位算法
相比于传统定位算法,基于多普勒和阵列处理的联合算法通过引入目标波达方位和距离信息,作为联合识别不同目标的标准,在检测性能上取得了较好的效果。但是,为了获取新的信息,该算法同时也对系统的硬件提出了更高的要求。因此,如何在保持雷达基础结构不变的基础上,有效提高雷达的检测精度和抗混淆能力成为一个迫切的问题。此外,从式(1)中可以看到,连续波穿墙雷达的检测性能很大程度上取决于雷达对目标多普勒频率的估测精度。而传统定位算法,乃至基于多普勒和阵列处理的联合算法,在对目标频率的估测问题上都是基于短时傅里叶变换的,并没有本质区别。而短时傅里叶变换,由于存在自身所固有的时间和频率分辨率的折中矛盾,是一种低精度的时频变换方法。因此,为提高目标多普勒频率的估计精度以及雷达在频率模糊区域内的抗混淆能力,文献[10]提出了一种基于2维频率拟合技术的定位算法,通过将目标频率拟合为一阶线性模型,从调制斜率和初始频率两个维度联合识别不同目标,以实现雷达在频率模糊区域内的准确定位。
3 基于高维拟合技术的恒虚警算法
基于2维拟合技术的定位算法在连续波穿墙雷达的目标识别问题上取得了令人满意的检测效果,但同时也存在着一定的不足。首先,该算法并未涉及对虚假目标的处理。在检测过程中,产生的虚假目标可能会对算法的最终定位结果产生较大影响。其次,基于2维拟合技术的定位算法采用一阶时间函数来模拟时窗范围内目标频率的变化。当目标的多普勒频率存在明显的非线性变化时,该模型可能会产生较大的拟合误差。最后,当回波不同分量间存在明显的幅度差异时,强分量的泄漏能量可能会对弱分量的相关检测产生一定的干扰,从而产生误差。因此,为了进一步提高雷达的检测性能,有必要针对上述问题对算法进行改进。
3.1 雷达恒虚警预处理
根据前面的分析,雷达检测过程中的虚假目标通常是由残留在处理信号中的噪声分量所引起的。由于实际探测环境复杂多变,固定的噪声阈值往往很难在不同的环境下同时兼顾系统的虚警和检测概率。因此,本文提出了一种雷达恒虚警处理技术,有效抑制了虚假目标的产生,其具体分析如下:
首先对雷达接收的回波信号进行Hilbert变化,将其转变为相应的复信号。然后根据经典的二值假定理论[11],若回波信号中包含有用的目标调制分量,则将回波状态记为H1,反之记为H0。
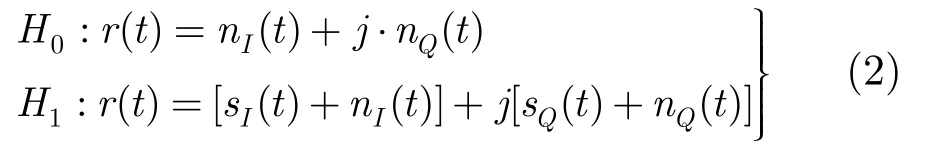
其中sI(t),sQ(t),nI(t)和nQ(t)分别为目标调制信号和复噪声信号的实部和虚部分量。在此,假设噪声服从高斯分布。则在H0状态下,回波信号的包络函数V(t)=|r(t)|服从瑞利分布,反之,V(t)服从莱斯分布,其概率密度[12]可分别表示为
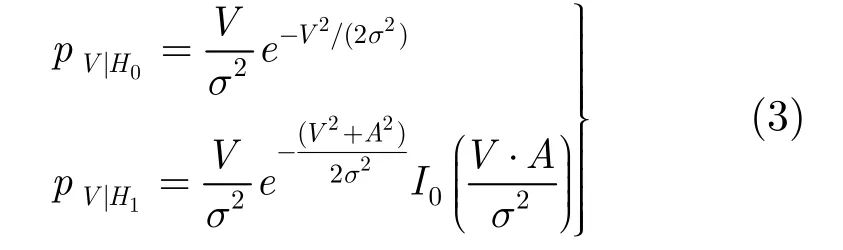
其中s为条件变量,I0(·)为0阶贝塞尔函数。
对r(t)进行短时傅里叶变换,并假设目标多普勒频率的变化区间为−fs~fs,其中fs为目标所能达到的最大频移。则在此区间外建立过渡频带f1<|f|<f2,其中相关参数满足fs<f1<f2。则显然过渡频带内的回波状态近似服从H0,条件变量s可由此估算为

其中E[V|H0]表示过渡频带内包络信号的均值。假设系统的噪声阈值为t1,则检测虚警概率为

若雷达的采样间隔为Δt,检测要求的平均虚警间隔为Tfa,则阈值t1可进一步表示为

3.2 基于高维拟合技术的自适应修正算法
为了进一步提升雷达的检测精度,本节在2维拟合算法基础上提出了一种基于高维拟合技术的自适应修正算法。该算法以2维拟合处理的结果为基础,为了抑制回波信号中强分量的泄漏能量对弱分量检测的干扰,算法在进行分量分离时,每次仅提取相应2维平面内的最强分量,并在估计弱分量的相关参数前,从处理信号中滤除了之前提取的强分量,从而保证了估计参数的准确性。
假设某一时窗范围内的回波信号经过前期的 2维拟合处理,已经被分解为M个独立分量。
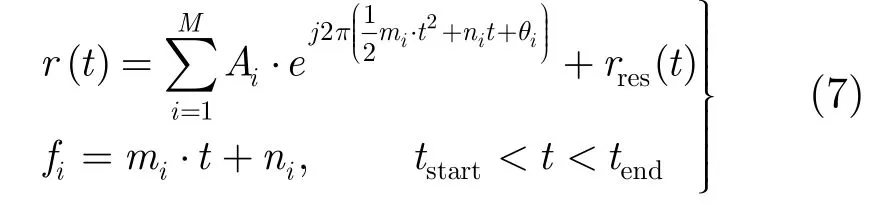
其中Ai,fi分别为第i个分量的幅度和频率,而mi,ni,分别为该分量所对应的调制斜率、初始频率和初始相位。rres(t)为拟合处理的残余回波分量。
计算残余回波的信号能量E,若E超出系统的预设阈值,则认为目标频率的拟合结果存在较大误差,需要进行高维的修正,否则即认为拟合精度达到了检测要求,并返回相应的估测值。
假设某一目标频率的2维拟合结果如图1(a)中的线L所示,未达到要求的检测精度。根据Weierstrass数值分析定理[13],任意高阶差分连续的函数曲线在足够短的时间范围内都可以统一用一段中心对称的凸曲线来进行任意精度范围内的逼近。因此,在图1(a)中用一段任意的对称曲线P来模拟该分量在时窗范围的频率变化轨迹。从图中可以看到,由于目标的频率轨迹存在较大的非线性变化,一阶线性模型无法准确描述其变化趋势,因此在时窗范围内,特别是在时窗函数的端点和中心位置,出现了较大的拟合误差。为减小误差,在3维拟合过程中,采用最简单的中心对称凸曲线——圆弧曲线来对目标的实际频率进行逼近。其拟合结果如图1(a)中的实线圆弧所示。
建立线L的中垂线L1,可表示为

其中t0为时窗的中心时刻点。以线L1上的某点为圆心,圆心到L端点的距离为半径,建立信号的3维拟合模型,其圆心坐标(t1,f1)及半径r可表示为
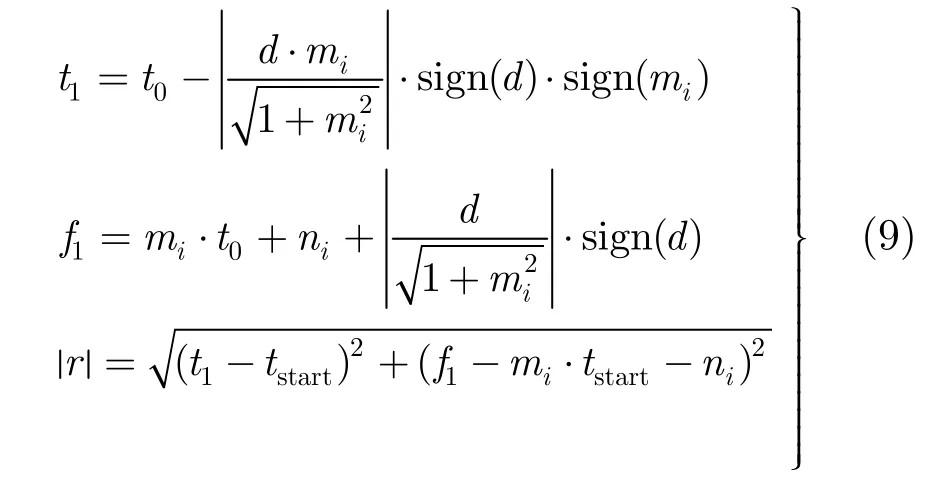
其中sign(·)为通用的符号算子,d为圆心到L中点的距离。则目标频率的3维拟合结果可表示为

调节参数d并按得到的拟合结果解调回波信号,直至其在频域达到最大收敛,如式(11)所示。
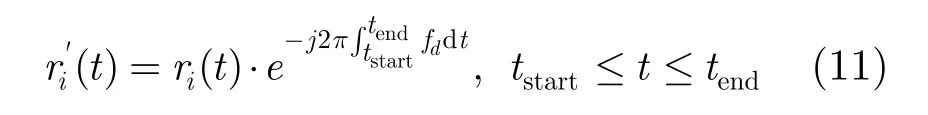
至此,目标频率的3维拟合结果如图1(a)中的实线圆弧所示,与其真实频率轨迹P间保持最接近恒定的距离D。最后,引入修正系数k,将信号的频谱峰值搬移至零点的位置。则式(10)可相应改写为

图1 高维频率拟合示意图

如图1(a)中的虚线圆弧所示。
同理,计算拟合所产生的残余能量,若依然大于系统阈值,则继续进行4维拟合处理。4维拟合采用更为复杂的椭圆模型,其基本思想与3维拟合相类似,如图1(b)示。参考图1(a)中的定义,图1(b)中的曲线P和L分别代表了目标频率的实际值及其3维拟合的结果。在 4维拟合处理中,在保持椭圆中心位置和长轴半径与3维模型的圆心和半径一致的基础上,通过改变椭圆短轴的长度r′,使其逼近目标实际的频率轨迹。因此,目标频率的4维拟合结果可相应表示为
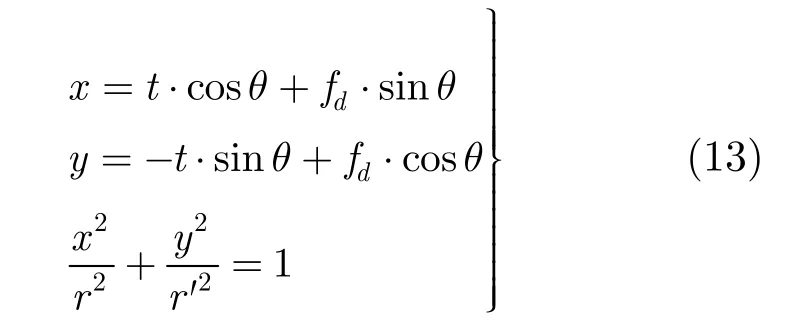
参考式(11)重新解调目标分量,并调整参数r′使解调后的信号在频域达到最大收敛,则目标频率的 4维拟合结果如图1(b)中的实线椭圆所示。引入修正系数k,调节拟合模型如图1(b)中的虚线椭圆所示,则目标多普勒频率的4维拟合结果可表示为
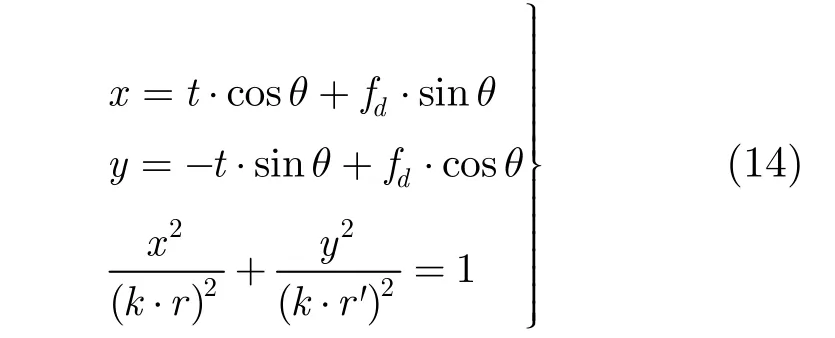
将估计得到的目标多普勒频率代入式(1)中,则可实现目标最终的精确定位。
4 实验与分析
为了验证本文提出的基于高维拟合技术的恒虚警目标定位算法的有效性和优越性,本节将通过实测数据,对比几种算法的相应检测结果,并进行分析。在此,为保证雷达双频发射的基础结构不发生改变,在对多普勒和阵列处理联合算法进行分析时,仅采用该算法对目标方位角的识别处理,而沿用短时傅里叶变换对目标距离的估测结果。
雷达样机所使用的载波频率分别为2.4 GHz和2.41 GHz,共包括1个发射和4个独立的接收单元,其天线阵列呈等间距的线性排列。间距约为6.5 cm。在处理过程中,除基于多普勒和阵列处理的联合算法使用全部4个接收单元外,其余算法均只使用最靠近发射机的2个接收单元,以保证系统的简洁性。在定位过程中,以发射机的位置为原点,平行墙体方向为x轴,建立坐标系,并选择0.5 s的汉明窗为分析时窗。
假设检测区域内存在两个运动目标,其中目标1以 2 m/s的速度水平从位置(-5,10)移动到(5,10)点,而目标2以0.4 m/s2的加速度沿雷达径向从位置(0,10),由静止状态均匀加速至(0,5)点。整个运动过程共持续5 s。不同算法的相关参数估计和定位结果分别如图2-图3所示。从图2中的参数估计结果中可以看到,基于多普勒和阵列处理的联合算法、2维拟合算法及高维拟合算法都能通过多维变量的联合识别,有效避免检测过程中的频率模糊效应。其中,基于多普勒和阵列处理的联合算法在目标方位角的检测上具有较高的精度。这是因为联合算法采用了4个接收单元的回波信号,与其它算法相比拥有接近2倍的信息量。然而,该算法检测性能的提升是以牺牲雷达的硬件成本为代价的,在实际应用中存在一定的局限性。此外,由于雷达只使用了两个载波频率,该算法在对目标距离的估测结果上出现了明显的误差。2维拟合算法无论在目标方位角还是距离的检测上,都具有较高的精度,能较准确地反映目标的运动轨迹。但在少数低信噪比时刻点,仍存在较明显的的误差。而高维拟合算法通过对 2维拟合结果的修正,进一步降低了检测误差,相比于其它算法,具有最好的参数估计精度。从图3的定位结果可以看到,基于短时傅里叶分析的传统算法,其检测精度是所有算法中最差的。这主要是由短时傅里叶变换所固有的时间和频率分辨率的折中矛盾所引起的。利用传统算法检测目标,观测者往往只能对目标位置进行一个粗略的观测,而很难得到某一时刻目标的精确坐标。而高维拟合算法的目标定位结果与其真实位置基本一致。此外,由于雷达接收的原始回波信噪比较低,因此在其对应的检测结果中出现了大量的虚假目标,严重影响了操作者对真实目标的识别。而在经过本文介绍的恒虚警算法处理后,虚假目标基本全部被滤除,增强了雷达定位结果的可靠性。
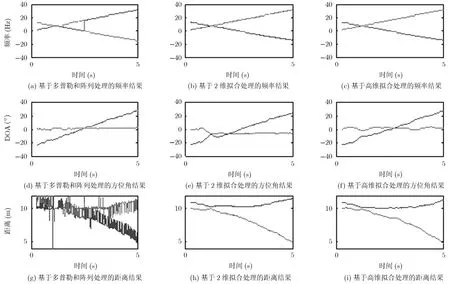
图2 参数估计性能比较
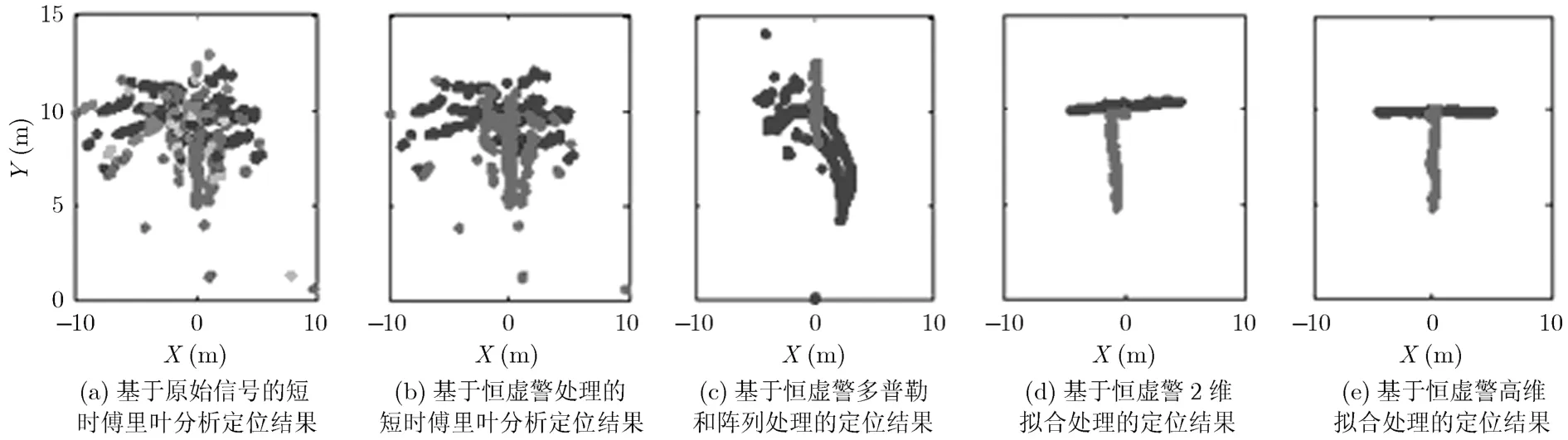
图3 定位性能比较
5 结束语
本文提出了一种基于高维频率拟合技术的恒虚警穿墙雷达定位算法。该算法以2维频率拟合处理的检测结果为基础,通过引入恒虚警和高维频率拟合技术,改善了困扰连续波穿墙雷达定位的高虚警和“频率模糊”问题,进一步提高了系统在不同检测环境下的识别适应能力。此外,该算法能在不额外增加系统硬件复杂度的前提下,根据检测的实际环境自适应地选择拟合维度,在保证要求的检测精度基础上,尽量减少了处理所需的时间,以适应雷达实时检测的需求。实验结果证明,采用本文提出的新算法,能有效提高穿墙雷达的检测精度和分辨能力,为连续波穿墙雷达的高精度定位提供可能。
[1] Li Y L, Zhang W J, and Li F. A novel auto-focusing approach for real-time through-wall imaging under unknown wall characteristics[J].IEEE Transactions on Geosciences and Remote Sensing, 2010, 48(1): 423-431.
[2] Wang Y Z, Yang Y Q, and Fathy A E. A reconfigurable UWB system for real-time through wall imaging applications[C].IEEE Radio and Wireless Symposium (RWS), New Orleans,LA, 2010, 3: 633-636.
[3] D’Urso M, Gianota F, and Lalli R,et al.. Differential approach for through-the- wall life signs detection[C]. 2010 IEEE Radar Conference, Washington, DC, 2010: 1079-1082.
[4] Amin M G, Zemany P, and Setlur P,et al.. Moving target localization for indoor imaging using dual freqeuncy CW radars[C]. IEEE Sensor Array and Multi-channel Processing,Waltham, MA, 2006: 367-371.
[5] Debes C, Riedier J, and Zoubir A M,et al.. Adaptive target detection with application to through-the-wall radar imaging[J].IEEE Transactions on Signal Processing, 2010,58(11): 5572-5583.
[6] Zhang Y, Amin M, and Ahmad F. A novel approach for multiple moving target localization using dual-frequency radars and time-frequency distributions[C]. Asilomar Conference. Signal, System and Computers, Pacific Grove,CA, 2007: 1817-1821.
[7] Ram S S, Christianson C, and Youngwook K,et al..Simulation and analysis of human micro-dopplers in throughwall environment[J].IEEE Transactions on Geosciences and Remote Sensing, 2010, 48(4): 679-699.
[8] Ram S S, Li Y, and Lin A,et al.. Human tracking using Doppler processing and spatial beamforming[C]. IEEE Radar Conference, Boston, MA, 2007: 546-551.
[9] Yu X G, Li C Z, and Lin J S. Two-dimensional non-contact vital sign detection using Doppler radar array approach[C].2011 IEEE Microwave Symposium Digest (MTT), Baltimore,MD, 2011: 1-4.
[10] Ding Y P and Fang G Y. New target detection algorithm for continuous wave through wall radar [J].Chinese Journal of Radio Science, 2010, 25(3): 590-596.
[11] 李道本. 信号的统计检测与估计理论[M]. 北京: 科学出版社,2005: 38-45.Li D B. The Statistical Theory of Signal Detection and Estimation [M]. Beijing: Press of Science, 2005: 38-45.
[12] Anderson M G. Design of multiple frequency continuous wave radar hardware and micro-Doppler based detection and classification algorithm[D]. Philosophy Department, The University of Texas, 2008.
[13] Rudin W. Principles of Mathematical Analysis [M]. 3rd Ed,New York: McGrwa-Hill, 1976: 169-230.

