基于ε-不敏感准则和结构风险的鲁棒径向基函数神经网络学习

桑庆兵 邓赵红 王士同 吴小俊

①(江南大学物联网工程学院 无锡 214122)

②(江南大学数字媒体学院 无锡 214122)

1 引言

在目前的建模方法中，径向基函数神经网络(Radius-Basis-Function Neural-Network, RBF-NN)建模是有效的方法之一[1−3]。经典的RBF-NN模型训练主要是基于最小平方误差准则的。该类训练算法存在的一个明显不足是：对于小样本数据集或存在噪声的数据集，训练容易过拟合，所得RBF-NN泛化能力较差[1,3]。因而，针对此问题探讨鲁棒的RBFNN训练新算法是一个很有意义的工作。

最经典的一类RBF-NN训练学习算法是基于梯度下降学习策略的。该类算法的缺点是由于学习步长选择的不合理或者由于基于经验风险陷入局部极值或过拟合而使受训网络的泛化性降低[1,3]。关于RBF-NN训练学习的最新重要研究进展是极速学习训练方法[4−10]，文献[4,11]指出输入层权值和隐层阈值任意选取的包含N个隐结点的单隐层前馈网络(SLFN)能够以任意小的误差逼近N个不同的观测值。基于以上理论，文献[4]针对单隐层神经网络提出了极速学习机(Extreme Learning Machine, ELM)算法，并进一步提出了各种改进的极速学习算法。ELM算法与常规的梯度下降学习算法相比，简单快速，在获得小的训练误差的同时，能获得较好的泛化能力。但是，针对小样本数据集和噪声，ELM算法依然鲁棒性较差，容易导致过拟合问题。

针对经典学习方法对小样本数据集和噪声数据容易过拟合而使得受训RBF-NN泛化能力较差的问题，本文通过引入e-不敏感学习度量[2,12−16]和结构风险项[2,13,15]来构造新的目标函数，并把提出的新目标函数求解转化为经典的二次规划问题。本文提出的方法由于引入了不敏感学习度量和结构风险项，能有效地克服经典训练算法针对小数据集容易过拟合和对噪音敏感之缺陷，显示出了较好的鲁棒性。在模拟和真实数据集上的试验亦证实了上述优点。

2 径向基神经网络

经典的径向基神经网络模型如图1所示[4]。径向基网络能完成非线性映射f:Rd→R1，其数学表达式为

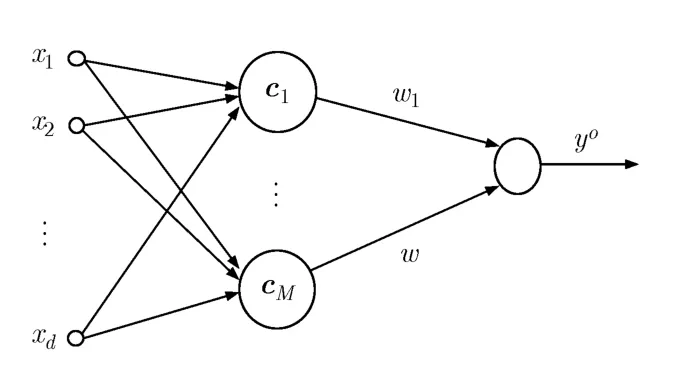
图1 RBF神经网络模型结构

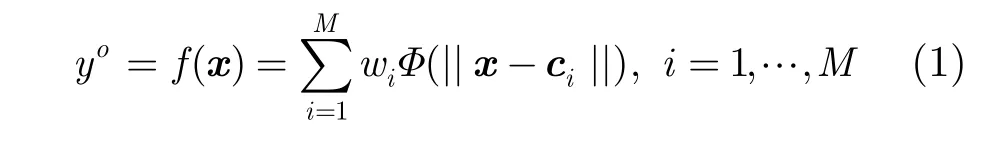
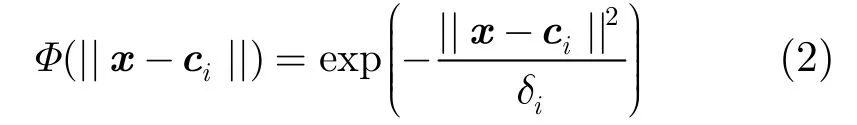
其中di为宽度值。

上述的径向基神经网络模型中，要学习的参数有3种，即隐层中心点，隐层径向基函数宽度值di，隐层和输出层的连接权值wi。对于径向基神经网络的各参数，最经典的一类训练学习算法是基于梯度下降学习策略的。但该类算法由于基于经验风险易于陷入局部极值或过拟合从而使受训网络泛化能力降低，而且此类算法由于是迭代算法，常具有很高的时间复杂度。另一类近年来较受关注的算法是极速学习机(ELM)算法。ELM算法与梯度下降学习算法相比，简单快速，在获得小的训练误差的同时，能获得较好的泛化能力。但是，针对小样本数据集和噪声，ELM依然鲁棒性较差，容易导致过拟合问题。针对此挑战，在后面一节，本研究将探讨一种鲁棒的基于不敏感准则和结构风险的径向基函数神经网络参数学习方法。

3 基于ε-不敏感准则和结构风险的径向基神经网络训练

3.1 径向基神经网络和线性模型

对于径向基神经网络的隐层中心点参数ci=和宽度参数di，一种常用的估计方法是聚类法。例如，利用模糊C均值(FCM)聚类技术，可利用下式来估计。

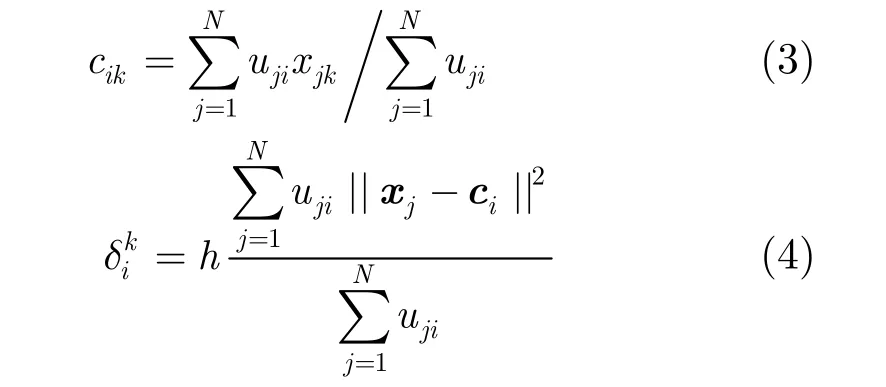
这里ujk表示 FCM 聚类方法得到的样本xj=对于第i类的模糊隶属度[1,3]；参数h是一个可调的缩放参数。

对于径向基函数神经网络，一旦隐层参数被估计，那么令

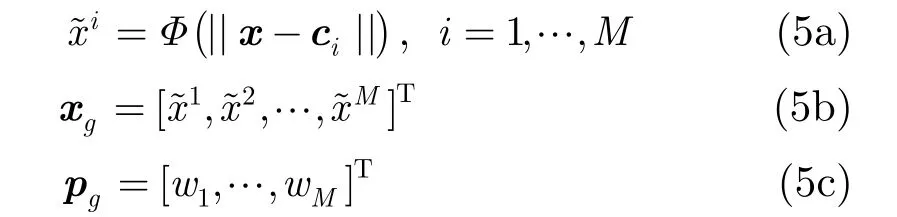
此时式(1)所示的径向基网络映射函数可表示为

由式(6)可知，当径向基网络的隐层节点被估计后，网络的输出可表示为一个线性模型的输出，此时网络参数的学习转化为线性模型之参数学习问题。基于此线性模型，本文通过引入e-不敏感误差准则和结构风险来构建新的径向基网络学习算法。

3.2 ε-不敏感误差准则

径向基神经网络训练时，常采用式(7)所示的最小平方差误差准则[1,3]：

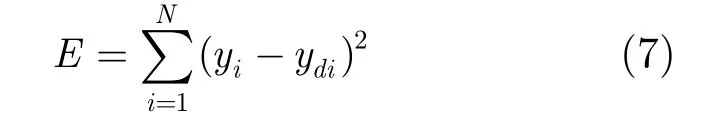
一般情况下，利用此准则能取得较好的效果。基于最小平方差误差准则的经典RBF-NN训练算法有基于梯度学习的方法[1,3]和极速学习方法[4−10]。但当数据样本较少且噪音较大时，此准则学习得到的网络对噪音较敏感，容易过拟合。基于此不足，本文引入了不敏感误差度量来设计新的径向基网络训练准则函数来增强网络的鲁棒性。

给定标量g和向量, 相应的e-不敏感损失分别具有式(8)，式(9)所示的形式[12−16]：

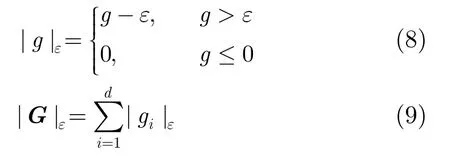
对于式(6)所示的线性模型，其对应的e-不敏感损失误差准则可定义如下：

3.3 基于ε-不敏感误差准则和结构风险的径向基网络训练

利用式(11)，式(10)所示的准则函数可等价地表示为

进一步地，参照支撑向量机等核方法[2]，引入结构风险正则化项，式(12)可改进为

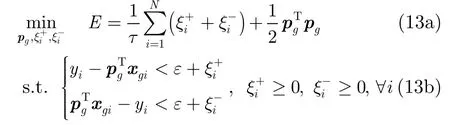
结构风险思想的引入，可进一步使得新算法像许多核方法一样，在小样本训练集环境下，所受训得到的网络具有较好的泛化能力，有效地避免过拟合问题。这里t＞0用来平衡经验误差项和表示结构风险的正则化项的影响。

在式(13)中有两个参数需要给定，即t,e需要给定。如何确定其最优值，目前还没有理论的解析公式可用。实际应用中，一个简单有效的策略是利用交叉验证法在某个参数集中来确定最优值。特别地，这里对不敏感参数e给出如下说明：该参数类似于支撑向量回归(SVR)方法中的不敏感参数e。SVR中该参数的理论研究表明[17,18]：该参数的最优值和数据中的噪声的方差呈现近似正比的关系，即噪声越大，该参数通常需采用较大的值来获得好的训练效果。在试验部分4.2节，我们对此结论给出了相关的实验验证。

特别地，对于式(13)，利用拉格朗日优化可得到其对偶问题(证明略)：

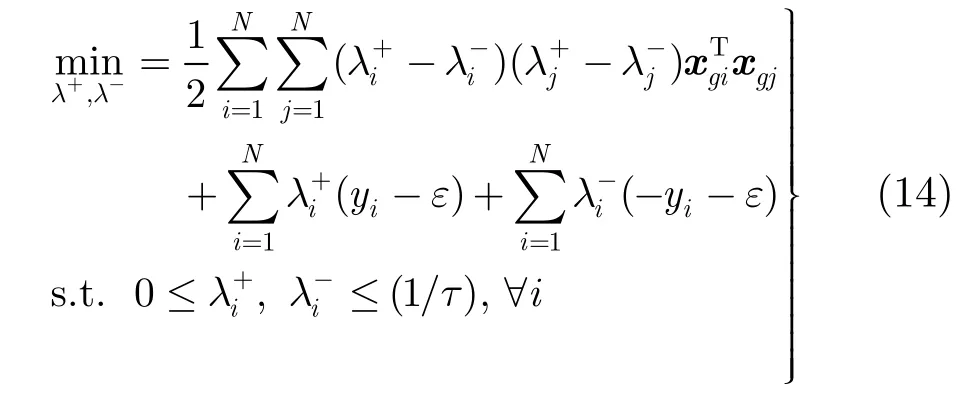
根据对偶理论，利用式(14)得到的最优解λ−∗,λ+∗，可得到式(13)对应的最优解为

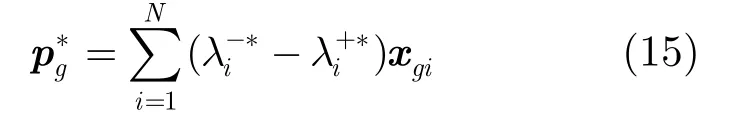
根据上面推导和分析可以看出：通过引入e-不敏感误差准则和结构风险项，RBF网络训练可以视为一个二次规划优化问题。因而已有的各种二次规划算法可以直接用来对RBF-NN 进行训练。

基于如上分析，容易给出基于e-不敏感准则和结构风险的RBF-NN训练新算法，如表1所示。

表1 基于ε-不敏感准则和结构风险的RBF神经网络训练算法

4 试验研究

本节对提出的新RBF-NN训练算法(表示为e-RBF)进行了试验测试。为了有效地评估算法性能，本文提出的算法和经典的基于平方误差准则的梯度学习算法(表示为LS-RBF)和极速学习算法(ELM)进行了比较。试验安排如下：(1)4.1节利用模拟数据集对算法性能进行了测试。(2)4.2节利用真实的煤气炉建模数据集对算法性能进行了测试。试验中，利用训练集采用了5倍交叉验证策略在集合中分别确定参数t,e的合适取值。

为有效评估该算法性能，采用了如下性能指标：

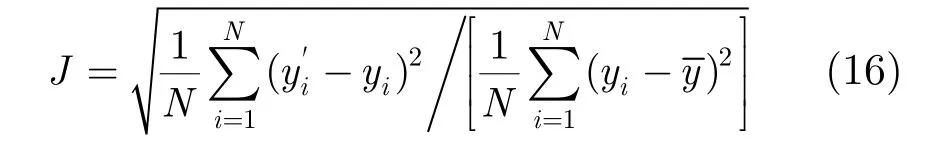
这里N是测试样本集的尺度；yi是第i个测试样本的采样输出，是第i个样本对应的神经网络输出，并且。J越小，表示建模(泛化)性能越好。

为了充分测试各算法对于噪声数据的鲁棒性，试验中对训练数据集加入了不同程度的高斯白噪声来进行鲁棒性测试。

4.1 模拟模数据集

本试验所用的数据集采样于如下的sinc函数[1]：

N( 0,s)表示均值为0，标准差为s的白噪声。利用式(17)产生包含200个数据的训练集，同时产生一个包含1000个数据且不含噪声的测试集。利用训练集来进行训练，然后利用测试集进行测试。上述过程重复10次，得到的平均测试结果来评价算法的性能。

图2和表2示出了噪音环境下3种算法在sinc数据集上的试验结果。从图 2和表 2，我们可得出如下的观察结果：

(1)当噪声较小时，几种不同方法展现出了可比较的泛化性能。

(2)随着噪声程度的增加，几种不同方法的泛化能力都逐步下降。

(3)在几种方法中，提出的基于e-不敏感准则和结构风险的新训练算法随着噪声的增加，泛化能力减弱的程度最小。特别是当噪声程度较大时，其泛化能力明显优于其它两种方法。

根据如上观察结果可知，针对该模拟数据提出的新算法在噪声环境下展现出了更好的适应能力。

4.2 Box-Jenkins(B-J)煤气炉真实数据集

本试验研究了 Box-Jenkins(B-J)煤气炉建模问题[19,20]。煤气炉控制输入u(k)表示气体进入熔炉的量，输出y(k)表示煤气炉中CO2的输出量，数据样本每隔9 s采样一次，共得到296组输入输出样本对。根据文献[1]中的方法，试验中选择u(k− 3)和y(k−1)作为输入变量，y(k)作为输出量重新构造数据集，得到290个有效数据对。把数据集随机分为训练集和测试集两部分，其中训练集和测试集尺寸分别为 145。对训练数据集加不同程度的噪声并利用训练集来进行训练，然后利用测试集进行测试。上述过程重复10次，得到的平均试验结果如图3和表3所示。正如同前一试验得到的观察结果，从图3和表3同样可以看出类似的实验效果：(1)采用不同数目的隐节点，提出的新训练算法在噪声较小时，展现了与经典的方法可比较的性能；(2)但当噪声加大时，提出的新算法展现了更好的鲁棒性，泛化性能明显优于其它两种经典算法。因而，在煤气炉真实数据集的试验结果表明，本文提出的基于e-不敏感准则和结构风险的RBF-NN训练算法，较之于经典的训练算法在噪声环境下展现出了更有希望的性能。

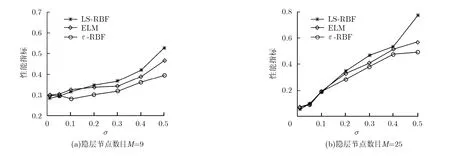
图2 采用不同数目隐节点时3种方法在sinc数据集上得到的的平均性能比较

表2 采用不同数目隐节点时3种方法在sinc数据集上得到的的平均性能比较

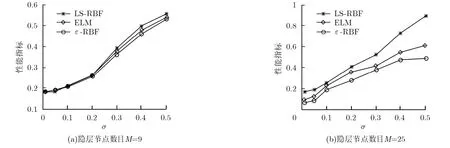
图3 采用不同数目隐节点时3种方法在煤气炉建模数据集上得到的的平均性能比较

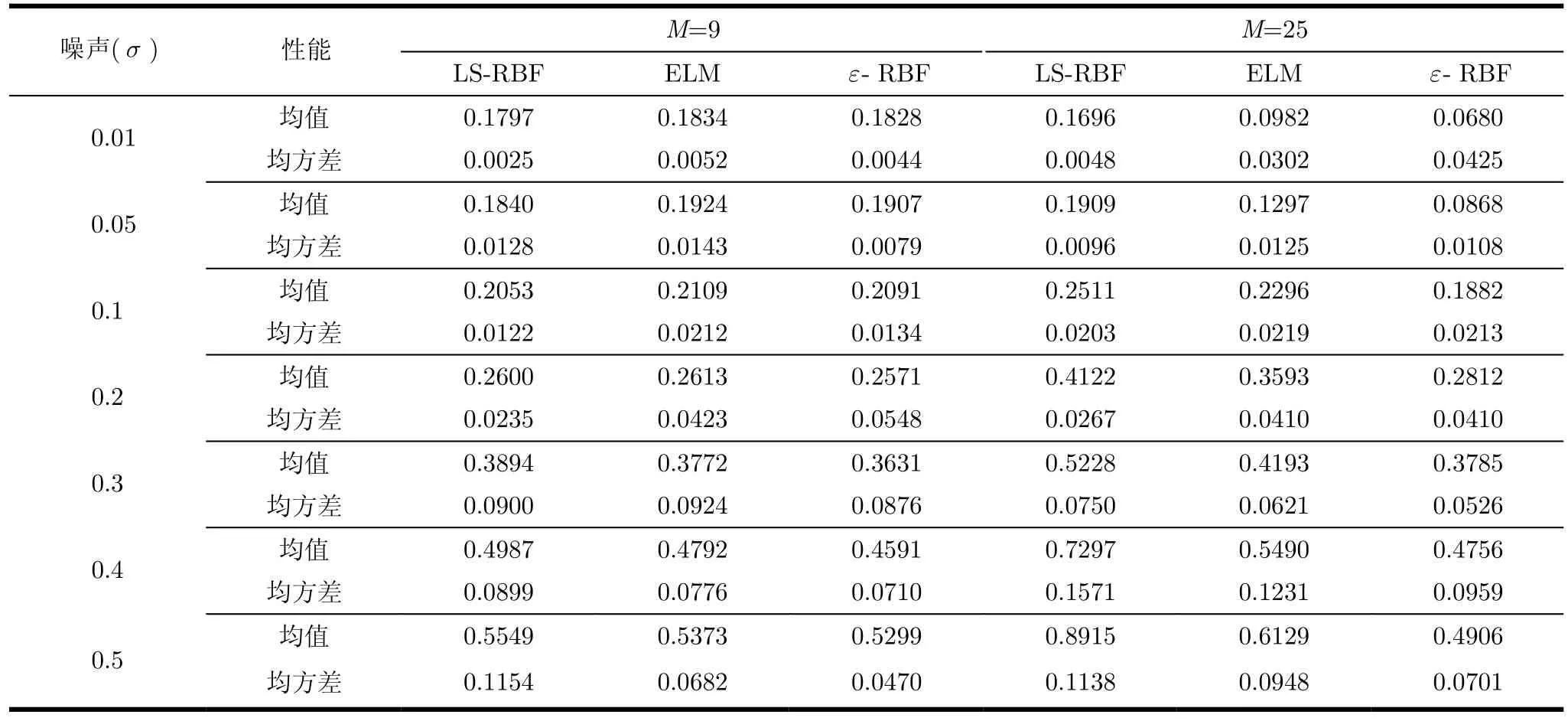
表3 采用不同数目隐节点时3种方法在煤气炉建模数据集上得到的的平均性能比较

4.3 不敏感参数ε的选择与噪音方差之间存在的比例关系

正如3.3节所述，文献[17,18]表明不敏感参数e的合适取值和噪声有一定的正比关系。这里我们利用实验进行简单验证。表4给出了实验中得到的最优不敏感参数e和噪声标准差s之间的关系。从表中我们容易看出，随着噪声的增加，最优的e取值也逐渐增加，即它们之间呈现近似的正比关系。值得指出的是，这里我们仅给出了简单的实验验证结果，如何从理论上证明上述结论是一个较复杂的工作，这需要借鉴文献[19,20]的相关研究思路来进行严格的数学分析，未来的工作中我们将对此作深入探讨。

表4 最优的不敏感参数ε和噪声之间σ的关系

5 结束语

本文通过引入e-不敏感准则和结构风险，把RBF-NN训练转化为线性回归问题，进而转化为经典的二次规划优化问题，提出了一种新的径向基神经网络建模方法。通过模拟和真实数据集进行仿真试验，提出的算法较之于传统的基于最小平方误差准则的算法对噪声数据集显示出了更鲁棒的性能。进一步地，基于计算智能研究方面的最新进展，提出适宜于大规模数据集的基于e-不敏感准则和结构风险的径向基神经网络快速训练算法值得探讨，未来的工作中，我们将对此进行深入研究。

[1] Jang J S R, Sun C T, and Mizutani E. Neuro-Fuzzy and Soft-Computing. Upper Saddle River, NJ, Prentice-Hall, 1997:125-134.

[2] Vapnik V. Statistical Learning Theory. New York: Wiley,1998: 256-396.

[3] 王士同, 等. 神经模糊系统及其应用. 北京: 北京航空航天大学出版社, 1998: 198-224.Wang S T,et al.. Neural Fuzzy System and Its Application.Beijing: Beijing University of Aeronautics and Astronautics,1998: 198-224.

[4] Huang G B, Zhu Q Y, and Siew C K. Extreme Learning Machine: Theory and Applications.Neurocomputing, 2006,70(1-3): 489-501.

[5] Cao J W, Lin Z P, and Huang G B. Composite function wavelet neural networks with differential evolution and extreme learning machine.Neural Processing Letters, 2011,33(3): 251-265.

[6] Huang G B and Wang D H. Advances in extreme learning machines (ELM2010).Neurocomputing, 2011, 74(16): 2411-2412.

[7] Lan Y, Soh Y C, and Huang G B. Two-stage extreme learning machine for regression.Neurocomputing, 2010, 73(16-18):3028-3038.

[8] Lan Y, Soh Y C, and Huang G B. Constructive hidden nodes selection of extreme learning machine for regression.Neurocomputing, 2010, 73(16-18): 3191-3199.

[9] Cao J W, Lin Z P, and Huang G B. Composite function wavelet neural networks with extreme learning machine.Neurocomputing, 2010, 73(7-9): 1405-1416.

[10] Huang Guang-bin, Ding Xiao-jian, and Zhou Hong-ming.Optimization method based extreme learning machine for classification.Neurocomputing, 2011, 74(1-3): 155-163.

[11] Huang G B. Learning capability and storage capacity of two-hidden-layer feed-forward networks.IEEE Transactions on Neural Networks, 2003, 14(2): 274-281.

[12] Leski J. Towards a robust fuzzy clustering.Fuzzy Sets and Systems, 2003, 12(2): 215-233.

[13] Leski J. TSK-fuzzy modeling based one-insensitive learning.IEEE Transactions on Fuzzy Systems, 2005, 13(2):181-193.

[14] 邓赵红, 王士同. 鲁棒的模糊聚类神经网络. 软件学报, 2005,16(8): 1415-1422.Deng Z H and Wang S T. Robust fuzzy clustering neural networks.Journal of Software, 2005, 16(8): 1415-1422.

[15] Deng Z H, Choi K S, Chung F L,et al.. Scalable TSK fuzzy modeling for very large datasets using minimal-enclosing-ball approximation.IEEE Transactions on Fuzzy Systems, 2010,18(2): 210-226.

[16] Deng Z H, Choi K S, Chung F L,et al.. Enhanced soft subspace clustering integrating within-cluster and betweencluster information.Pattern Recognition, 2010, 43(3):767-781.

[17] Kwok J T and Tsang I W. Linear dependency between epsilon and the input noise in epsilon-support vector regression.IEEE Transactions on Neural Networks, 2003,14(3): 544-553.

[18] Wang S T, Zhu J G, Chung F L,et al.. Theoretically optimal parameter choices for support vector regression machines with noisy input.Soft Computing, 2005, 9(10): 732-741.

[19] Box G E P and Jenkins G. M. Time Series Analysis,Forecasting and Control. 2nd Ed, San Francisco, CA, Holden Day, 1976: 355-390.

[20] Chung F L, Deng Z H, and Wang S T. From minimum enclosing ball to fast fuzzy inference system training on large datasets.IEEE Transactions on Fuzzy Systems, 2009, 17(1):173-184.