斜井段钻柱混沌运动的数学模型与参数

刘杏培，王晓阳

(兰州交通大学数理与软件工程学院，甘肃兰州 730070)

斜井段钻柱混沌运动的数学模型与参数

刘杏培，王晓阳

(兰州交通大学数理与软件工程学院，甘肃兰州 730070)

基于现代动力系统理论，对斜井段钻柱的复杂动力学行为进行研究．通过考虑由于弯曲变形而产生的附加轴向力，得到描述井孔约束下斜井段钻柱在周期性钻压作用下的非线性参数激励系统，利用Melnikov-Holmes方法得到钻柱发生混沌运动的判据，并结合具体工程实例分析了倾斜井钻柱混沌运动的参数激励阈值，所得结论在钻井工程中具有较强的可操作性．

钻柱；斜井；混沌运动；数学模型；参数

当今社会经济飞速发展，对石油产品的需要与日俱增．钻柱的工作状态是否稳定直接关系着定向井钻井作业的成败．弄清钻柱的失效原因，对延长钻柱的工作寿命、缩短钻井周期、降低钻井成本具有重要意义．近年来，钻柱动力学分析是研究热点，受到有关学者的广泛关注[1]．针对钻柱失效问题，2004年，李子丰建立了力激励法和位移激励法的数学模型[2]，2007年，张治勇建立了动力学模型和方程[3]．本文应用现代动力系统理论，对斜井段钻柱在波动钻压下的非线性振动进行理论研究，推导出钻柱发生混沌运动的判据，并对参数激励阈值进行了分析，以期为合理调整钻井作业参数给出理论依据．

1 控制方程的建立

图1 钻柱微元受力图

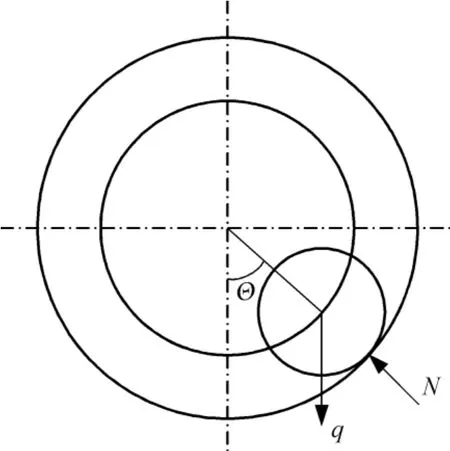
图2 钻柱的侧向屈曲

2 控制方程的求解

根据Melnikov方法，钻柱进入混沌运动的判据可表示为：为激励阻尼比，与阻尼比有关，可根据现场具体情况测出．

3 工程实例

由本文所推导的结论，将以上数据带入（4）式，得系统进入混沌运动的阈值为：

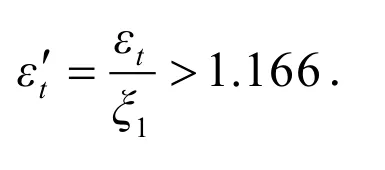
图3 钻压-激励阻尼比变化示意图

4 结 论

（1）本文基于现代动力系统理论，对分析模型进行了比较合理的简化，推导出的一系列常数适用于斜直井段钻柱.

（2）钻柱的混沌运动多数要依靠钻井经验和实际情况作初步的判断，本文提供的方法明确针对此问题，所得结论在钻井工程中具有较强的可操作性．

（3）由图3可知，随着稳定部分钻压数值的增加，激励阻尼比迅速减小，而实际工程中特定工况下的激励阻尼比是确定的，因而产生混沌的可能性迅速增加，充分显示了预知临界钻压的重要性.

[1] 胡以宝. 钻柱动力学研究及监控技术新进展[J]. 石油钻探技术, 2006, 34(6): 7-10.

[2] 李子丰. 钻柱纵向和扭转振动分析[J]. 工程力学, 2004, 21(6): 203-210.

[3] 张治勇. 钻柱失效的动力学分析[J]. 西部探矿工程, 2007, 2: 78-79.

[4] 焦永树. 石油钻井工程中钻柱的静力动力分岔研究与混沌运动分析[D]. 天津: 天津大学机械工程学院, 1998: 12-30.

[5] 刘锋. 无量纲化的方法[J]. 安顺学院学报, 2008, 10(3): 78-80.

[6] 李荣华. 微分方程数值解法[M]. 北京: 高等教育出版社, 2005: 15-32.

Mathematical Model and Parameters of Drill String’s Chaotic Motion in Slant Hole Interval

LIU Xingpei, WANG Xiaoyang
(School of Mathematics, Physics and Software Engineering, Lanzhou Jiaotong University, Lanzhou, China 730070)

Based on theory of modern dynamic system, complicated dynamic behaviors of drill string were studied. Considering the extra axial force aroused by the lateral deformation, a non-linear parametrically excited system was established to describe the action of drill string (leashed by the wellbore in slant hole) under periodical weight-on bit. Then making use of Melnikov-Holmes method, the threshold value of the parameter excitation that can trigger chaotic motion of the drill string was obtained. In addition, relevant conclusions of parametric excitation threshold were obtained by analyzing the chaotic motion of slant drill string in engineering practice. The achieved conclusions have more practicable operability in drilling project.

Drill String; Slant Hole; Chaotic Motion; Mathematical Model; Parameter

O322

A

1674-3563(2012)06-0032-04

10.3875/j.issn.1674-3563.2012.06.006 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2011-05-19

刘杏培(1982- )，女，河北衡水人，硕士研究生，研究方向：非线性振动理论及应用