基于虚拟样机技术的货车车架疲劳寿命预估

北京航空航天大学交通科学与工程学院 王得长 李 强

北京福田戴姆勒汽车有限公司 王 凌

1.前言

疲劳失效是引起机械机构失效的主要原因之一，其危险性表现在结构到达疲劳寿命时无明显征兆（显著变形）就会突然断裂。

因此，为了保证产品可靠的工作，合理的制定使用寿命至关重要[1]。传统的分析方法采用对汽车零部件进行大量的台架试验和整车耐久性试验，不仅成本高、周期长，而且只能在样车制造出以后进行，对设计更改带来一定的难度[2]。

与基于试验的传统方法相比较，有限元疲劳仿真可以在设计阶段得到零部件表面的疲劳寿命分布情况，到疲劳寿命危险点，进而对产品进行优化，可以缩短产品的研发周期，降低成本。车架作为汽车零件的重要组成部分，其功用是承担连接汽车的各零部件，并承受来自车内外的各种载荷。其抗疲劳性能直接影响车辆的安全性和可靠性，要求其具有足够的强度和适当的刚度且质量小。

本文以某中型双轴载货汽车为研究对象，综合利用ADAMS和Hypermesn软件，分别建立其多体动力学模型和有限元模型，在虚拟环境中得到车架的疲劳寿命，为车辆的轻量化设计提供理论依据。

2.整车多体动力学模型的建立及载荷谱获取

本文以北京汽车集团有限公司生产的某中型载货汽车为研究对象，该车满载试验质量为9360kg，长、宽、高依次为6740mm、2128mm和2300mm，轴距为3800mm。为了获得车架在不同路况下受到的动载荷，在ADAMS中建立整车多体动力学模型如图1所示，其包括由车身、驾驶室、货物及其它附件刚性连接到车架上的簧载质量部分，车轮系，前后悬架，路面等。该模型共有11个自由度，分别为四个车轮的垂向运动，四个钢板弹簧的俯仰运动，车身的垂向、侧倾、俯仰运动。前后钢板弹簧刚度由公司提供，依次为372kN/m和748kN/m，前后减震器阻尼根据悬架的相对阻尼为0.3算得，依次为6.8kN·s/m和11kN·s/m。考虑到轮胎的阻尼极小，将其简化为线性弹簧元件[3]，轮胎的刚度由其尺寸计算得到，前轮为单胎，刚度为1860kN/m，后轮为双胎，总刚度为3400kN/m。

将整车模型在各级道路上进行仿真，在各级道路行驶里程所占比例按照我国相应道路所占总里程的比例确定[4]，对应车速按公司经调研后给出的推荐值。总里程取1km，则各等级道路的仿真里程和车速如表1所示。

将整车模型按表1所示的速度和时间进行仿真，得到汽车在不同等级道路上行驶时悬架对车架的动载输入。将采集到的数据点进行合并，得到整个仿真路况的载荷谱，其中前悬架左侧钢板弹簧和后悬架右侧钢板弹簧与车架相连处载荷历程分别如图2、图3所示。

3.有限元模型的建立及静强度分析

3.1 建立有限元模型

在Hyperwork平台中建立车架有限元模型，如图4、图5所示，根据车架纵梁和横梁的特点，对板件选取平均尺寸为10mm的壳单元进行网格划分，对于铸件用四面体单元模拟，驾驶室、发动机等部件均用集中质量来描述，并用RBE3单元将其连接到车架上，对于螺栓联接，用刚性单元处理，车厢及货物以均布载荷的方式作用在纵梁的上表面，模型共包括90530个节点，83297个单元。

为了模拟汽车在不同道路上行驶时不同路面对车架的冲击，动载系数的范围一般取1.8-2.5，现取最大值为2.5[5]。根据汽车厂家提供的参数，算得汽车的簧载质量为8500kg（其中前轴3453kg，后轴5047kg），于有G=8500×9.8=83300N。因此车架受到的最大冲击载荷Fmax=2.5×83300=208250N。车架材料选用的是16Mn钢，其常规力学性能：

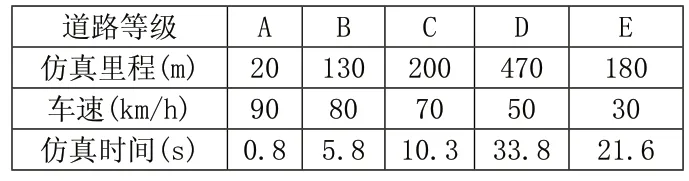
表1 各等级道路行驶仿真里程和车速

表2 16Mn钢试样50%存活率下的疲劳寿命

图1 整车多体动力学模型

图2 前悬左侧钢板弹簧安装位置动载

图3 后悬右侧钢板弹簧安装位置动载

图4 车架有限元模型

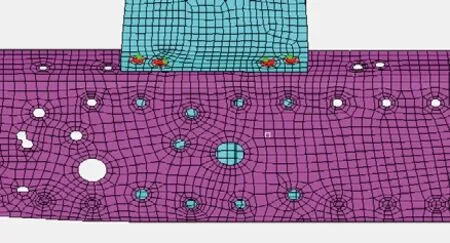
图5 局部放大图

表中：σ为应力，N50为50%存活率下的疲劳寿命。屈服强度为345MPa，泊松比为0.3，弹性模量为20600MPa。

3.2 静强度分析

图6 最大动载下应力分布图

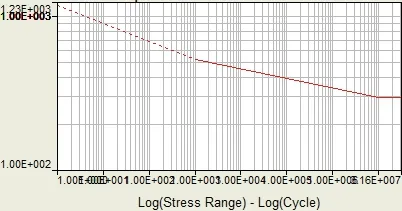
图7 双对数坐标下16Mn钢的S-N曲线

图8 车架疲劳寿命云图

图9 疲劳寿命最小区域寿命云图

将车架受到的最大冲击载荷按比例作用在车架与悬架相连处，并将这些位置的6个自由度约束。对上述有限元模型进行计算，模型的总体应力分布云图如图6所示。由图6可知：整个车架的总体应力较小，只是在部分区域存在应力较集中现象，大应力区域主要集中在第三根横梁与纵梁相连处以及后悬架支架与纵梁相连的螺纹孔处，约为260MPa，小于材料的屈服极限345MPa，说明该车架的静强度指标符合设计要求。

4.车架疲劳寿命仿真

该车架材料采用16Mn钢，在《机械工程材料性能数据手册》[6]中可得到16Mn钢50%存活率下的疲劳寿命，如表2所示。

另外，16Mn钢试样存活率为50%的疲劳极限是327MPa。Hypermesh中采用中，幂指数方程描述S-N曲线：

式（1）中：SRI是S-N曲线y轴的插值，b是斜率[7]。由表1可得：SRI=792.5MPa，b=－0.06097。利用这两个参数，考虑车架零部件疲劳缺口系数、尺寸系数、表面质量系数，对车架材料的S-N曲线进行修正[8]。在Hypermesh软件中进行自定义生成16Mn的S-N曲线如图7所示。

采用Goodman图对平均应力的影响进行修正[9]。求得的车架疲劳寿命云图如图8所示。结果显示，疲劳寿命最小区域位于后悬架支架与纵梁相连的螺纹孔及其附近的工艺孔处，如图9所示。危险点的疲劳寿命是约为70万km，超过了国家经济贸易委员会、国家发展计划委员会、公安部、国家环境保护总局1998年修改后的中型载货汽车报废标准——行驶40万km里程，可以对该货车进行轻量化设计。

5.结论

建立了汽车的多体动力学模型，并根据中国的路况进行多体动力学仿真，获取了车架受到的来自悬架的载荷历程；建立了车架的有限元模型，并基于该模型进行车架的静强度分析，综合有限元模型和车架受到的载荷历程进行车架的疲劳寿命预估，有限元仿真结果表明，车架的静强度符合设计要求，疲劳寿命最小区域位于后悬架支架与纵梁相连的螺纹孔及其附近的工艺孔处，疲劳寿命最小处的疲劳寿命达到中型货车报废标准，并且存在一定的富裕情况，可以为该货车进行轻量化设计。

[1]熊峻江.疲劳断裂可靠性[M].北京:国防工业出版社,2008.

[2]孙凌玉.利用计算机仿真技术预测车身零件疲劳寿命[J].汽车工程,2001,23(6):389-392.

[3]余志生.汽车理论[M].北京:机械工业出版社,2009.

[4]中华人民共和国国家统计局.中国统计年鉴[M].北京:中国统计出版社,2010.

[5]耿作恒等.汽车车架焊接支座的疲劳分析[J].电焊机,2010,40(5):145-149.

[6]《机械工程材料性能数据手册》编委会.机械工程材料性能数据手册[M].北京:机械工业出版社,1995:101-102.

[7]王国军.疲劳分析实例指导教程[M].北京:机械工业出版社,2009.

[8]RAHMAN M.M.,ARIFFIN A.Effects of surface finish and treatment on the fatigue behavior of vibrating cylinder block using frequency response approach[J].Journal of Zhejiang University SCIENCE A,2006,7(3):352-360

[9]刘鸿文.材料力学[M].北京:高等教育出版社,2011.