广义逆矩阵｛2｝-逆充分必要性的一些新结论

范庆民

（太原理工大学 数学学院，太原030024）

近几十年来，由于广义逆矩阵在统计学、测量学、经济学以及计算数学、控制论和系统分析、优化理论等众多领域中有着广泛的重要应用，从而促使广义逆矩阵的理论、计算方法和应用的研究迅速发展［1－4］。笔者基于相关的广义逆矩阵理论，得到满足一定条件的｛2｝-逆充分必要性的一些新结论。

1 术语与符号

设，Cn为复n 维向量空间，Cm×n为复m×n阶矩阵的集合，Cm×nr＝｛A∈Cm×n，rank A＝r｝。R（A）＝｛y∈Cm：y＝Ax，x∈Cn｝为A 的值域，N（A）＝｛x∈Cn：Ax＝0｝为A的零空间。AH表示A 的共轭转置矩阵。S⊥表示子空间S的正交补。

对Cn中任意两个子空间L和M，若Cn＝L⊕M，则称Cn的子空间L和M 为互补的。这时，任意x∈Cn都可惟一分解为

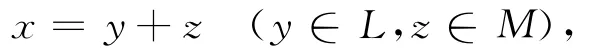
称y为x沿着M到L的投影。

用PL，M表示将任意x∈Cn变为沿着M 到L的投影的变换，即PL，Mx＝y。易知此变换为线性的，也是幂等的，称变换PL，M为沿着M 到L的投影算子，称沿着L⊥到L的投影算子PL，L⊥为正交投影算子，记为PL。

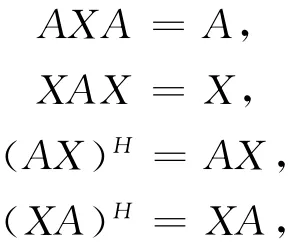
定义1.1［5］设A∈Cm×n，如果X∈Cn×m满足则称X 为A 的 Moore-Penrose广义逆，记为A＋。称定义1中的四个方程为Moore-Penrose方程。由于这四个方程都各有一定的解释，并且在很多领域的实际应用中也各有方便之处［6－8］，所以出于不同目的，常要考虑满足部分方程的X。

定义1.2［5］设A∈Cm×n，用A｛i，j，…，l｝表示所有满足 Moore-Penrose第i，j，…，l个方程的矩阵X∈Cn×m的集合。矩阵 X∈A｛i，j，…，l｝记作 X＝A（i，j，…，l），称为 A 的｛i，j，…，l｝－逆。

2 已有的相关结论

定理2.1［9］设A∈Cm×n，则

1）（A（1））H∈AH｛1｝；

2）rank A（1）≥rank A；

3）若P和Q 为非奇异矩阵，则Q－1A（1）P－1∈（PAQ）｛1｝；

4）AA（1）和A（1）A 是幂等矩阵，且有

rank AA（1）＝rank A ＝rank A（1）A；

5）（A＋）＋＝A；

6）（AH）＋＝（A＋）H；

7）设P∈Cn×n为幂等矩阵，则Px＝x，当且仅当x∈R（P）。

定理2.2［9］如果A（1）∈A｛1｝，则

R（AA（1））＝R（A），

N（A（1）A）＝ N（A），

R（（A（1）A）H）＝R（AH）.

定理2.3［10］对任一幂等矩阵P∈Cn×n，R（P）与N（P）为互补子空间，则

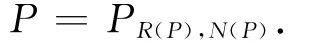
反之，如果L与M 为互补子空间，则存在着惟一的幂等矩阵PL，M，使得R（PL，M）＝L，N（PL，M）＝M.

定理2.4［10］设Cn＝L⊕M，A∈Cn×n，则

1）PL，MA＝A，当且仅当R（A）⊂L；

2）APL，M＝A，当且仅当N（A）⊃M.

定理2.5［11］对任意给定的矩阵A，A＋是满足X∈A｛1，2｝和R（X）＝R（AH），N（X）＝N（AH）的惟一矩阵。

定理2.6［11］设 A∈Crm×n，R（A）＝L，N（A）＝M，L⊕S＝Cm，且M⊕T＝Cn，则AT（1，S，2）＝PT，MA（1）PL，S是A的惟一具有值域T和零空间S的｛1，2｝-逆。

定理2.7［11］设A∈Crm×n，U∈Cn×p，V∈Cq×m，X＝U（VAU）（1）V，则

1）X∈A｛2｝且，R（X）＝R（U），当且仅当

rank（VAU）＝rank U；

2）X∈A｛2｝且，N（X）＝N（V），当且仅当

rank（VAU）＝rank V；

rank（VAU）＝rank U ＝rank V＝r.

3 满足一定条件的｛2｝-逆的充分必要性结论

定理3.1 设A∈Crm×n，T为Cn的s（≤r）维子空间，再设S为Cm的m－s维子空间，那么A有满足R（X）＝T和N（X）＝S的｛2｝-逆，当且仅当

这时，X是惟一的。

证明 充分性。设U∈Cn×ss的列为T 的一组基，VH∈Cm×ss的列为S⊥的一组基。则AU的列生成AT。因为从（1）可推知dimAT＝s，故

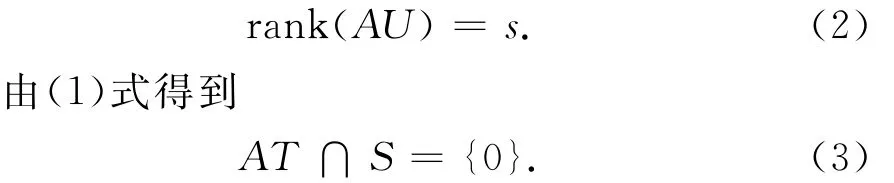
而且，s×s矩阵VAU非奇异，这是因为VAUy＝0，所以AUy⊥S⊥，即AUy∈S.

由（3）式有 AUy＝0；

又由（2）式有 y＝0.

因此由定理2.7得

X ＝U（VAU）－1V.

它为A的一个有值域T和零空间S的｛2｝-逆。

必要性。因为A∈X｛1｝，由定理2.1的4）知AX是幂等的。而且由定理2.2

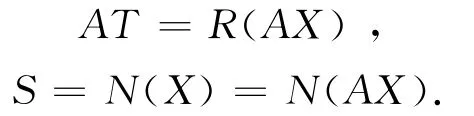
于是（1）式可从定理2.3推出。

唯一性。设X1，X2为A的具有值域T和零空间S 的｛2｝-逆，由定理2.1的4）和定理2.2，X1A为具有值域T的投影算子，而AX2为具有零空间S的投影算子，于是由定理2.4有

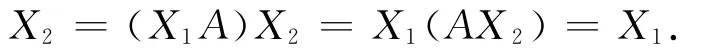
推论3.1 设A∈Crm×n，S和T 分别为Cm和Cn的子空间，使得

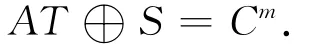
令AT（2，S）表示A的惟一具有值域T和零空间S的｛2｝-逆，则

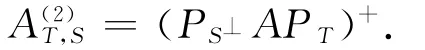
推论3.2 设A∈Crm×n，T为Cn的r维子空间，且S为Cm的m－r维子空间，于是下述三种论述是等价的。

1）AT⊕S＝Cm；

2）R（A）⊕S＝Cm，N（A）⊕T＝Cn；

3）存在着一个X∈A｛1，2｝，使得R（X）＝T，N（X）＝S.

定理3.2 设 A∈Cm×n，X∈Cn×m，则 X∈A｛2｝，当且仅当X 为形如X＝（EAF）＋的矩阵。其中E与F为适当的Hermite幂等阵。

证明 充分性。由定理2.5有R（（EAF）＋）⊂R（F），N（（EAF）＋）⊃ N（E）.因此，由定理2.4

X ＝ （EAF）＋＝F（EAF）＋＝ （EAF）＋E，于是

XAX ＝ （EAF）＋EAF（EAF）＋＝ （EAF）＋＝X.

必要性 由定理2.5和定理2.6有

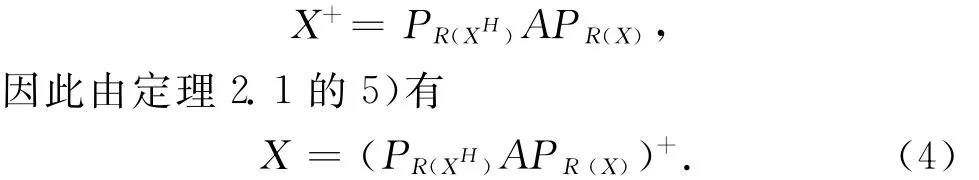
等式（4）可叙述为，如果X∈A｛2｝，则X为通过将A的列投影到R（XH），其行投影到R（X）上所得到 Moore-Penrose逆。

定理3.3 设P为Hermite幂等矩阵，则X∈P｛2，3，4｝，当且仅当X 为 Hermite幂等矩阵，且R（X）⊂R（P）。

证明 充分性。因R（X）⊂R（P），由定理2.1的7）有PX＝X，取其共轭转置就有XP＝X。由于X是Hermite矩阵，所以PX与XP均为Hermite矩阵。又因为X是幂等的，所以XPX＝X2＝X。于是，X∈P｛2，3，4｝。

必要性 设 X∈P｛2，3，4｝，则 X＝XPX＝PXHX，因此R（X）⊂R（P）。又由定理2.1的7）有，PX＝X，因为X∈P｛2，3｝，故PX 为 Hermite幂等矩阵。因此X是Hermite幂等的。

［1］ 陈永林.矩阵的扰动与广义逆［J］.应用数学学报，1986，9（2）：319-327.

［2］ Kalaba R E，Rasakhoo N.Algorithm for generalized inverse［J］.J Optimization Theory and Applications，1986，48：427-435.

［3］ 王玉文，李志伟.Banach空间中 Moore-Penrose广义逆与不适定边值问题［J］.系统科学与数学，1995，15（2）：175-185.

［4］ 倪仁兴.Moore-Penrose广义逆和最佳逼近算子的表达式［J］.工程数学学报，2005，22（1）：175-178.

［5］ Horn R A，Johnson C R.Matrix Analysis［M］.Landon：Cambridge University Press，1985.

［6］ 张显，曹重光.关于域上矩阵广义逆的加法映射［J］.数学学报，2004，47（5）：1013-1018.

［7］ 范庆民.矩阵广义逆在动态解藕模糊控制系统中的应用研究［J］.太原理工大学学报，2007，38（2）：180-182.

［8］ Heinig G.Generalized inverses of Hankel and Toeplitz mosaic matrices［J］.Linear Algebra Appl，1995，216：43-59.

［9］ Nashed M Z.Generalized Inverses and Applications［M］.New York：Academic Press，1996.

［10］ Rajendra，Bhatia.Matrix Theory［M］.New York：Springer-Verlag，INC，1997.

［11］ 程云鹏，张凯院，徐仲.矩阵论［M］.西安：西北工业大学出版社，2000.