基于Gauss伪谱法的高超声速飞行器多约束三维再入轨迹优化
姚寅伟 李华滨
北京航天自动控制研究所,北京 100854
高超声速再入飞行器利用气动力在大气层边缘长距离滑翔,全程机动飞行。再入飞行过程中受到如气动、热流等严格的过程约束;同时,再入初始状态根据任务的不同会有较大变化,而且飞行过程中会根据信息链更改滑翔结束点的使用状态。因此,针对此类飞行器需要在飞行过程中进行在线轨迹规划。这就要求优化算法既要满足一定的计算精度,又要满足快速性的要求。
近几年发展起来的伪谱法(Pseudospectral Method),以其求解精度高和收敛速度快的特点,在复杂的最优控制问题中得以广泛的应用。根据离散点的选取方式不同,常见的伪谱方法有Legendre伪谱法、Gauss伪谱法。其中,通过Gauss伪谱法转化的NLP(Nonlinear Programming Problem非线性规划问题)求解的KKT(Karush-Kuhn-Tucker最优化条件)条件和连续最优控制问题的一阶必要条件相同,这一点优于Legendre伪谱法[1]。影响伪谱法计算精度和收敛速度的主要因素有: 1)参数初值; 2)离散节点的数量。因为伪谱法能够以较少的节点数量获得较精确的解[2],所以影响伪谱方法的主要因素就是参数初值。采用随机算法求解NLP,如遗传算法,粒子群算法等,这类方法不依赖参数初值的选取,但是计算时间长,无法满足快速性的要求。文献[3]提出一种从可行解到最优解的串行优化策略,以较少的Gauss节点进行优化得到的可行解作为初值[3],然后采用具有超一次收敛性的SQP方法求解NLP,但初始节点的选取仍然要人为选取,不具有在线自主规划的能力。
在现有的快速轨迹规划方法中,文献[4]中所述方法能够快速计算一条满足各种过程约束和状态约束的三维再入轨迹,但其横向轨迹设计部分仅通过一次改变倾侧角的符号进行控制,不太适用于大范围横向机动情况。
因此,本文在现有研究成果的基础上,采用拟平衡滑翔条件结合横向误差走廊的方法计算满足各种约束的三维再入轨迹,作为高斯伪谱法的初值,弥补了算法对初值的敏感性。然后采用“Gauss伪谱+SQP”的优化方法,进一步求解满足各种约束、同时使性能指标最小的再入轨迹,最后对通过数值积分的结果和优化的插值计算结果进行比较,分析了此方法的有效性。
1 再入轨迹优化问题
1.1 无动力再入运动模型
最优控制问题的数学描述一般要求给定自变量的初始值和终端值,对于轨迹优化来说,初始时刻是已知的,但终端时刻无法确定,因此引入反值能量e代替时间作为自变量,其表达式为:
e=1/r-V2/2
(1)
它随时间单调变化,符合作为自变量的要求,而且只要已知再入初始和终端的状态,运动方程就可在固定自变量区间[e0,ef]内进行积分计算,满足轨迹优化算法的要求。e对无量纲时间τ求导得:
(2)
再入飞行过程中,假设地球模型为均质圆球,考虑地球旋转,侧滑角为0,采用式(1)所述的能量e代替时间作自变量,可得再入飞行器无量纲三自由度运动方程:
θ·
(3)

(4)

(5)
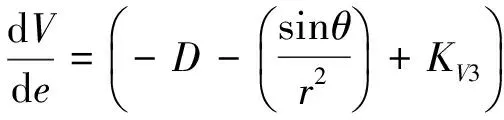
(6)
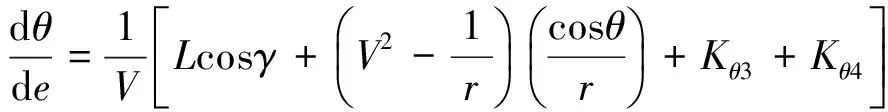
(7)

(8)
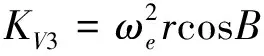
Kθ3= 2ωeVcosBsinA

KA3= 2ωeV(tanθcosAcosB-sinB)


L=RmρV2SrefCL/2m
D=RmρV2SrefCD/2m
(9)
ρ为大气密度;Sref,m分别为飞行器参考面积和质量;CL,CD是与α相关的升力系数和阻力系数。
1.2 再入轨迹约束条件
(1)飞行过程约束
根据飞行器结构和外形的特点,飞行过程中需要满足:热流约束、动压约束、过载约束、给定攻角下的平衡滑翔条件,即:
≤
(10)

(11)
n=Lcosα+Dsinα≤nmax
(12)

(13)
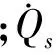
(2)终端约束
再入滑翔段的终端状态同时也是末段制导的初始状态,根据末段制导的要求,滑翔段终端状态需要满足一定约束,即位置约束(包括地心距rf、经度λf、纬度Bf)和速度约束(包括速度大小Vf,弹道倾角θf,航向角Af),其表达式为:
r(e)f=rf,λ(e)f=λf,B(e)f=Bf
(14)
|V(e)f-Vf|≤ΔV,|θ(e)f-θf|≤Δθ
|A(e)f-Af|≤ΔA
(15)
“Δ”表示各终端状态允许的误差范围,根据飞行任务的不同,部分状态约束条件可忽略(如:弹道倾角、航向角等)。
(3)控制量约束
飞行过程中,为防止控制量过大,需要对其限幅,即:
|γ(e)|≤γmax
|α(e)|≤αmax
(16)
1.3 轨迹优化性能指标
选取飞行过程总的气动加热为优化指标,目标函数表达式为对驻点热流密度的积分,即:
(17)
2 高斯伪谱轨迹优化方法
2.1 基本原理
高斯伪谱法将状态变量和控制变量在一系列高斯点上离散,并以这些离散点为节点构造拉格朗日插值多项式来逼近状态和控制变量。通过对全局插值多项式求导来近似状态变量的导数,从而将微分方程约束转换为一组代数约束。性能指标中的积分项由高斯积分计算。终端状态也由初始状态和右函数的积分获得。经上述变换,可将最优控制问题转化为具有一系列代数约束的参数优化问题,即非线性规划问题(NLP)。
2.2 连续最优控制问题的离散
(1)区间变换
高斯伪谱法是在[-1,1]区间内通过Lagrange多项式拟合状态量和控制量,因此需要对原积分区间[e0,ef]进行区间变换,用自变量τ代替e:

(18)
变换后,得到新的区间τ∈[τ0,τf]=[-1,1]。轨迹优化问题可描述为Lagrange型的最优控制问题:
1)根据方程(17)得到目标函数:
τ
(19)
2)根据方程(3)~(8),得到状态方程:
τ(τ),U(τ),τ)
(20)
3)根据方程(14)和(15),得到边界条件
g(X(τf),τf)=0
(21)
4)根据方程(10)~(13)飞行过程约束
h[X(τ),U(τ),τ]≤0
(22)
(2)状态变量和控制变量的近似
高斯伪谱法对轨迹进行离散处理,选取N个Legendre正交多项式PN(τ)的零点(Legendre-Gauss点)τk(k=1,2,…,N)和起始点τ0=-1,终端点τf=1作为节点,构成Lagrange插值多项式,并以此为基函数构造状态变量和控制变量的近似表达式,即:
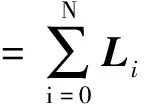
(23)

(24)
其中Lagrange插值基函数:
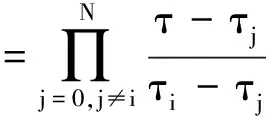
(25)

(26)
x(τ)是节点τ=τi(i=0,1,…,N)处的状态量,u(τ)是节点τ=τk(k=1,2,…,N)处的控制量。由式(23)~(26)可以得到,在节点处,实际状态量(控制量)与近似状态量(控制量)相等,即X(τi)=x(τi),U(τk)=u(τk)。
末端节点因为要满足微分方程约束,因此不能用上述插值多项式近似表达,按下式计算:
ωkF(x(τk),u(τk),τk)
(27)
其中,ωk为高斯权重,计算公式为[6]:

(28)
(3)微分方程约束的转化
对式(23)进行求导:
τk)≈(τ)x(τi)
(29)
其中微分矩阵D∈RN×(N+1)可以离线确定,即:
τk)
(30)
利用式(29)代替离散点处微分方程的左边式,从而将微分方程约束转换成代数约束:

(31)
其中k=1,2,…,N。
(4)性能指标函数的近似
将Lagrange型性能指标函数中的积分项用Gauss积分近似,得:
τk)
(32)
经过上述变换,基于高斯伪谱法的最优控制问题可以描述为:已知初始点的状态x0,求离散点上的状态变量xi和控制变量ui(i=1,2,…,N),使性能指标(32)最小,并且满足微分方程约束(31)和终端状态约束(27),以及原最优控制问题的边界条件
g(xf,τf)=0
(33)
和飞行过程约束
h[xk,uk,τk]≤0(k=1,2,…,N)
(34)
从而将原最优控制问题转化为一个一般的非线性规划问题(NLP),即:
s.t.gj(x)≥0,j=1,2,…,p
hj(x)≥0,j=1,2,…,l
(35)
其中,x为设计变量,包括6个状态变量和倾侧角、攻角2个控制变量,p为边界条件个数,l为过程约束个数。
2.3 高斯伪谱法求解NLP问题的方法
目前,求解NLP的方法中,SQP算法是公认的最有效的算法之一。它具有整体收敛性和局部超一次收敛性[7]。因此,本文采用SQP算法对上述NLP进行求解。
3 初值轨迹计算方法
在实际应用过程中,Gauss伪谱法对待优化参数初值较敏感,初值的好坏直接影响算法的收敛速度和计算精度,即初值越接近最优解,算法收敛越快。而接近最优解的必要条件是满足各种约束,因此,本文不考虑性能指标,只考虑满足飞行过程约束和终端状态,快速计算一条三维再入轨迹,在其上选择一系列离散点作为Gauss伪谱法待优化参数的初值。
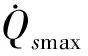
3.1 初始下降段
初始下降段在高度-速度(r-V)剖面内不满足平衡滑翔约束。因此要轨迹快速平滑地过渡到平衡滑翔状态,即:
δ
(36)

(37)

3.2 拟平衡滑翔段
(1)纵向轨迹计算方法
由于初始下降段结束后,飞行器达到平衡滑翔状态,因此采用基于拟平衡滑翔条件的方法计算滑翔段纵向再入轨迹。
忽略地球旋转的条件下,不考虑横向运动,剩余航程对能量微分的表达式为:
θ·
(38)
将式(38)与式(6)相除,满足平衡滑翔条件(13)时,θ≈0,可近似得到:
(39)
假设平衡滑翔起点和终点对应的剩余航程分别为stogo0和stogo1,将倾侧角的大小设计为速度的分段线性函数:
(40)
其中,V0和V1分别表示滑翔段初始点和终点的速度;γ0和γ1分别表示滑翔段初始点和终点的倾侧角;Vmid=0.75V1表示中间速度,γmid表示Vmid所对应的倾侧角的大小,为待优化变量。将式(39)在区间[stogo0,stogo1]内积分得到的末速度随倾侧角γmid单调变化[3],因此通过割线法搜索满足剩余航程要求的γmid。因为γ1是根据平衡滑翔条件和滑翔段终点的地心距和速度求出,所以当滑翔终点速度满足终端约束后,滑翔终点地心距亦满足约束。
(2)横向轨迹计算方法
纵向轨迹计算得到了倾侧角的大小,横向控制则通过改变倾侧角的符号来完成。对于航程远,横向机动大的再入飞行器,单次或者两次反号可能无法实现轨迹的精确控制,因此,本文采用航向角误差走廊控制倾侧角符号的变化,即航向角误差超出设定值就改变倾侧角符号。
4 数值仿真实例
数值仿真程序包括初值轨迹生成和高斯伪谱优化,均在C++环境下编写,计算机CPU为Inter(R)Core(TM)2 Duo 3.0GHz。
4.1 轨迹初值对Gauss伪谱法收敛速度的影响
表1为高斯伪谱法的滑翔飞行段终端状态允许偏差,也是算法收敛的退出条件。表2给出了对应不同轨迹初值时,Gauss伪谱法在满足表1的收敛条件下的迭代次数。

表1 终端状态允许偏差

表2 Gauss伪谱法在不同轨迹初值下收敛的迭代次数
从表2中可以看出在横向状态(经度、纬度、航向角)偏差基本相等的情况下,初值轨迹的纵向状态(高度、速度)偏差越小,算法迭代次数越少。其中初值轨迹4是采用本文第3部分所述的方法计算得到,相对于其他3个终端状态偏差较大的轨迹初值而言,从收敛速度上有明显优势。
4.2 Gauss伪谱优化再入轨迹数值仿真
1)初始状态:
[h0,λ0,B0,V0,θ0,A0]=[55km,30°,5°,5000m/s,-1°,90°]
2)终端状态:
[hf,λf,Bf,Vf,θf,Af]=[32km,55.24°,4.53°,2000m/s,0°,92.14°]
以再入全程总吸热量最小作为性能指标,如式(17)所示。Gauss节点数N=30。初值轨迹采用表2中的4号轨迹。终端状态收敛条件同表1。
图1~图4给出了数值仿真的结果,图例中Initial表示初值轨迹;GP表示节点,是Gauss伪谱法的设计变量;GPM表示通过Gauss伪谱法优化出的节点插值得到结果;ODE表示将插值得到的控制量代入原运动方程积分得到的结果。图1表示高度曲线,初值轨迹,即表1中的4号轨迹,接近最终优化后的轨迹,因此,算法迭代次数较少,整个优化程序在第4部分所述计算机环境下运行时间小于10s,说明该初值算法与Gauss伪谱法相结合的方法在优化快速性上具有一定优势,可行有效。图2表示经纬度曲线,即地轨迹。由图1和图2可以看出优化后的结果和积分得到的结果基本一致,说明高斯伪谱法对实际运动模型的近似具有较高的精度。图3和图4分别表示控制量倾侧角和攻角。表3列出了优化算法对于飞行过程的满足情况,可以看到:所有约束均小于允许值。而且只要算法收敛,即说明算法满足表1所示的终端状态约束,因此,Gauss伪谱法优化得到的结果满足所有约束。
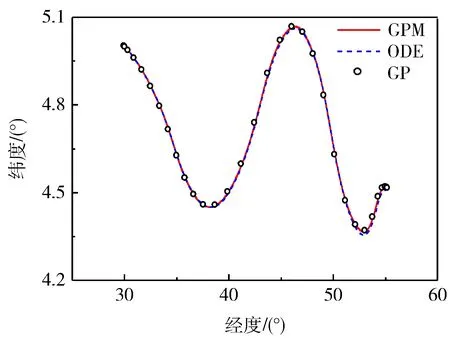
图2 经度-纬度曲线

图3 能量-倾侧角曲线
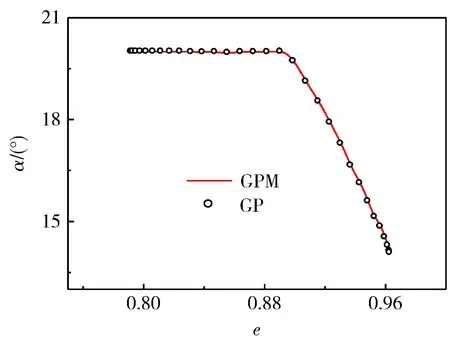
图4 能量-攻角曲线

表3 过程约束
5 结论
研究了临近空间高超声速飞行器的三维再入轨迹的快速优化方法。采用以能量作为自变量的运动方程,结合“初值轨迹生成+高斯伪谱法+SQP求解NLP”的优化方法,相对于一般不含初值生成的直接法,能以较少的迭代次数收敛,提高了算法的计算速度。通过对优化得到的结果和数值积分得到的结果进行比较分析,验证了算法的实际可飞性。本文提出的方法可作为快速轨迹优化方法的理论储备,同时可以作为下一步制导问题的基础。
参 考 文 献
[1] David Benson.A Gauss Pseudospectral Transcraption for Optimal Control [D].Doctor Dissertation of Massachusetts Institute of Technology, 2005: 109-111.
[2] Huntington G T.Advancement and Analysis of a Gauss Pseudospectral Transcription [D].Cambridge, MA: Massachusetts Institute of Technology, 2007.
[3] 雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D].长沙:国防科学技术大学,2008:49-50, 58-60.
[4] Zuojun Shen, Ping Lu.On-board Generation of Three-dimensional Constrained Entry Trajectories [J].AIAA Guidance, Navigation, and Control Conference and Exhibit.Monterey, California, 2002-4455.
[5] 胡正东.天基对地打击武器轨道规划与制导技术研究[D].长沙:国防科学技术大学博士论文,2009,120-123.
[6] 宗群,田栢苓,窦立谦.基于Gauss伪谱法的临近空间飞行器上升段轨迹优化[J].宇航学报,2010,31(7):1776-1780.(Zong Qun, Tian Bai-ling, Dou Li-qian.Ascent Phase Trajectory Optimization for Near Space Vehicle Based on Gauss Pseudospectral Methods[J].Journal of Astronautics, 2010,31(7):1776-1780 (in Chinese).)
[7] Philip E G.An SQP Algorithm for Large Scale Constrained Optimization [J].SIAM Review, 2005, 47(1):99-131.

