Blow-up流形的Gromov-Witten不变量的一个为零定理*

戚晓霞

(中山大学数学与计算科学学院,广东 广州510275)

1 Gromov-Witten不变量及其退化公式

1.1 GW-不变量

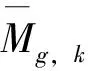
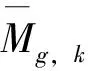
c1(A)+(n-3)(1-g)+k

(1)

其中c1是X的第一陈类。

给定α1,…,αk∈H*(X),定义GW-不变量为

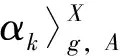
其中{αi}应满足维数条件：∑degαi=2c1(A)+2(n-3)(1-g)+2k,否则定义不变量为0。

1.2 相对GW-不变量

设D⊂X为X中一个光滑除子,即一个余维-2的辛子流形,且D是J-全纯的，即J(TD)⊂TD。给定A∈H2(X)满足A·D≥0，则相对J-全纯曲线的模空间为

u*[Σ]=A,Σμi=A·D,

u-1(D)=Σμiyi,μ=(μ1,…,μr)}

c1(A)+(n-3)(1-g)+k+r-A·D

(2)

给定α1,…,αk∈H*(X),β1,…,βr∈H*(D),定义相对GW-不变量为

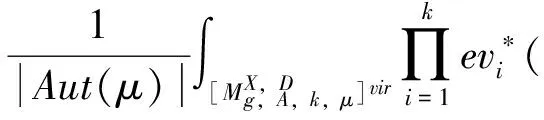
1.3 辛切割及退化公式

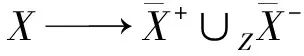
使得π|XH-1(0)=id，并且π|H-1(0)是商映射H-1(0)→Z。考虑

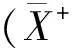
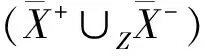
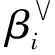
命题1[11-12]

(3)

命题2[11]

dimCM++dimCM-=dimCM+(n-1)l(μ)

(4)

2 主要结果及其证明

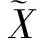
其中n≥3，r>0，p!=PD∘P*∘PD。

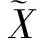
⊕O)，≅

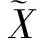
(5)

其中μ=(μ1,…,μl(μ))是E·(p!(A)+re)的一个划分，{βj}是H*(E)的任一组自对偶基底。这里E+应该被看作是P1-丛PE(O(-1)⊕O)的无穷截面，而E+≅E-≅E。

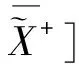
(p!(A)+re)+=aL+be,a≥0,b≥0

∑μi=H·(p!(A)+re)+=a

(6)

因为E+·(p!(A)+re)+=-r，于是

-r=E·(p!(A)+re)+=a-b

(7)

因此由(6)-(7)式得,b=∑μi+r，所以(p!(A)+re)+=∑μiL+(∑μi+r)e。

(1-g+)+k+l(μ)-∑μi=

[(n+1)H-(n-1)E]·[∑μiL+(∑μi+r)e]+

(n-3)(1-g+)+k+l(μ)-∑μi=

n∑μi+(n-1)r+(n-3)(1-g+)+k+l(μ)

不妨假设

∑

如果00，那么

另一方面,由维数关系(4)得

(n-2)l(μ)-n∑μi=

n(l(μ)-∑μi)-2l(μ)<

由GW-不变量的定义，(5)式右边每一项的第二个不变量都为零，因此(5)式为零。 □

注1 我们同时证明了n=2的情况，即当W(α)满足0

注2 定理1是对文[10](Proposition3.1)的推广,我们这里证明了对任意辛流形以及g≥0的结果,并且当g=0时，扩展了W(α)的取值范围。

参考文献：

[1]RUAN Y.Topological sigma model and Donaldson-type invariants in Gromov theory[J].Duke Math J,1996,83 (2): 461-500.

[2]RUAN Y,TIAN G.A mathematical theory of quantum cohomology[J].J Diff Geom,1995,42(2):259-367.

[3]BEHREND K.Gromov-Witten invariants in algebraic geometry[J].Invent Math，1997,127 (3): 601-617.

[4]FUKAYA K,ONO K.Arnold conjecture and Gromov-Witten invariant[J].Topology,1999,38 (5): 933-1048.

[5]LI J,TIAN G.Virtual moduli cycles and Gromov-Witten invariants of algebraic varieties[J].J Amer Math Soc,1998,11 (1): 119-174.

[6]LI J,TIAN G.Virtual moduli cycles and Gromov-Witten invariants of general symplectic manifolds [G].Topics in Symplectic 4-manifolds (Irvine,CA,1996),First Int Press Lect Ser,I,Int Press,Cambridge,MA,1998: 47-84.

[7]RUAN Y.Virtual neighborhoods and pseudo-holomorphic curves[J].Tr J Mathematics,1999,23: 161-231.

[8]LERMAN E.Symplectic cuts[J].Math Res Lett,1995,2: 247-258.

[9]HU J.Gromov-Witten invariants of blowups along points and curves[J].Math Z,2000,233: 709-739.

[10]GATHMANN A.Gromov-Witten invariants of blow-ups[J].J Alg Geom,2001,10: 399-432.arXiv:math/9804043v2

[11]LI A,RUAN Y.Symplectic surgery and Gromov-Witten invariants of Calabi 3-folds[J].Invent Math,2001,145 (1): 151-218.

[12]HU J,LI T,RUAN Y.Birational cobordism invariance of uniruled symplectic manifolds[J].Invent math,2008,172: 231-275.