基于体数据变形的自适应移动立方体算法的研究*
谢祚海,赵 颖,樊晓平,2,周 筠
(1.中南大学信息科学与工程学院,湖南 长沙 410075;2.湖南财政经济学院网络化系统研究所,湖南 长沙 410205)
近些年来,体数据可视化技术在医疗诊断、地质学和逆向工程等领域的应用日益增多,新的理论成果和实践操作不断产生,体数据可视化技术的实用性和针对性逐渐增强[1]。移动立方体(Marching Cubes)算法由Lorensen和Cline[2]提出,它通过对体数据中的体素抽取逼近等值面的三角面片,能够较好较快的对二维图像进行三维重建,因此在许多领域得到了广泛应用。当体数据的采样密度比较大、体素大小相对显示尺度很小时,这种简单构造三角片的方式足以满足实际使用中的精度要求,但是在处理采样密度较低的体数据时,重建的效果很难满足所需精确度的要求。目前国内外学者针对这一问题已有较多研究工作。Weber等[3]采用了对体数据中的网格进行多次迭代划分,从而使得数据场采样密度变大的方法;Ying 等[4]对体数据采用八叉树细分法,但是该方法会在部分区域产生空隙;Paiva等[5]提出的自适应网格法则是使用代数函数对抽取出的三角网格进行调整。这些研究主要是通过增加网格模型的顶点,也就是采样点的数量来提高三维数据场采样密度,从而确保三维重建所要求的精确度,但是采样点数量的增多也就意味着算法在三维重建时需要更多的内存更大的计算量。为了能够在不增加采样点数量的前提下,提高三维重建的精确度,可以采取预先对体数据变形的方式,而体数据的变形主要通过对体素顶点进行位移操作来实现。在此基础上,Congote等[6]提出了以迭代位移的方式对体数据进行变形,提高绘制图像精确度的方法;但是该方法在算法稳健性以及保证重建过程的实时性和交互性方面存在着缺陷。本文提出了一种基于体数据变形的自适应移动立方体算法,在处理采样稀疏的体数据时,首先分割体数据,去除与算法无关的体素;然后以自适应地改变三维数据场中感兴趣区域内体素顶点位置的方法对体数据进行变形,使得体素内包含的三角面片更加逼近等值面。在体素顶点位移的过程中,为了确保了拓扑结构不发生改变,使用了位移约束条件。并且利用GPU计算框架CUDA对算法进行了效率优化[7],从而确保重建过程具备较好的实时性和交互性。
1 移动立方体算法及待改进点
规则的体数据是三维空间中某一个区域中的采样,且采样点在x,y,z三个方向的分布是均匀的。因此体数据可以用三维数字矩阵来表示,即v(i,j,k)。移动立方体算法处理的基本单元是立方体或体素(Voxel),它是逻辑上的立方体,由相邻层上对应的四个采样点组成八个顶点。移动立方体算法的本质是从一个三维的数据场中抽取出一个等值面,所以也被称为等值面提取(Isosurface Extraction)算法。在三维体数据中被等值面包围的部分及为感兴趣区域(ROI)。等值面是空间的具有某个相同值的点的集合,它可表示为
{(x,y,z)|f(x,y,z)=T} ,T为常数
(1)
移动立方体算法的基本思想是:逐个遍历数据场中的所有体素,判断体素的八个顶点与所要求的等值面的内外关系,在与等值面相交的体素中,采用线性插值法计算出等值面与体素的交点。然后,根据体素顶点和等值面之间的内外关系,再将等值面与体素的交点按照一定方式连接成三角面片,作为等值面在该体素内的一个逼近表示[2]。
尽管移动立方体算法本身能够很好地实现三维重建功能,但还是存在着不足。在构造等值面时,它是用三角形面片拟合逼近等值面的方式来实现的,但等值面是一个三次曲面,等值面与体素面的交线是一条双曲线[2],如果体素很小,这种近似是可以忽略的,但由于体数据的采样密度是任意的,构造的体素大小也是有多种可能,在采样密度比较低、体素不够小的情况下,抽取出的三角面片与等值面存在差异[8],从而达不到重建所要求的逼近精度要求,影响重建效果。
2 基于体数据变形的自适应移动立方体算法
对于采样密度稀疏的体数据,本文提出先对体数据进行分割,提取出感兴趣区域内的体素,再通过对体数据进行变形的方式来提高重建的精确度,同时保证体数据的拓扑结构不变。
2.1 体数据分割
本算法需要对体数据中感兴趣区域内体素的顶点进行位移,从而使得体素包含的三角面片精确度更高。在这一过程中,位于感兴趣区域外的体素与算法无关,因此,对体数据进行分割可以避免不必要的计算,很好地提高算法的效率。
尽管传统的移动立方体算法大多采用阈值分割法对待重建的体数据进行处理[9],但它仍然存在着许多缺点,比如说分割的不是很准确、图像内部信息的丢失等等。所以,本文采用了交互式区域生长法,为了搜索感兴趣区域内的体素,在选取种子点后,使用区域增长的方法来搜索体数据[10-11]。采用区域增长的策略主要涉及到种子点选取和其它元素加入种子点集合的策略。种子体素选取就是根据指定阈值选取一个或一些体素,然后从这个或这些体素出发,寻找感兴趣区域内所有体素。先找到具有要抽取等值面的器官或者物体轮廓的片层,对该片层进行边沿提取,这些边沿点和这些边沿点所在层次的上一层的点形成的体素为候选种子体素。阈值计算的方法为:设选择的边沿点为p1,p2,…,pn,各点的灰度值分别为f(p1),f(p2),…,f(pn),那么等值面的阈值为
(2)
对于所选择的候选种子体素先根据计算出的阈值进行判断,那些不含有等值面的体素从我们所选择体素中剔除,剩余的体素为种子体素。
种子点集合增长的方法为:对一个位于感兴趣区域内的体素,它的一个或多个面上有一条等值边,则在与这一个或多个面上相邻的体素也是位于感兴趣区域内,将其加入感兴趣区域内体素的集合;反之,它的六个面均未与等值面相交,则它的所有相邻体素也是位于感兴趣区域内。本文中体数据分割的步骤为:
1) 选取种子点,计算阈值,形成种子体素,加入感兴趣区域内体素队列;
2) 按层次顺序从感兴趣区域内体素队列中取出体素,计算出其与等值面相交信息;
3) 根据体素等值面的信息找到没有入队的相邻的体素入队,转2);
4) 当遍历完所有体素后,体数据分割结束。
2.2 体数据变形
本文引入了体数据变形的方式对稀疏的体数据进行三维重建前的预处理,以防止出现三角面片与真实等值面之间存在过大差异,提高拟合逼近后的等值面的精确度。在体数据变形后必须满足:1)体素内的三角面片更加逼近等值面;2)保证体数据原来包含的拓扑结构不变。
假定一个稀疏体数据集为Q,等值面阀值为T,则重建的等值面为
S={v|f(v)=T}
(3)
其中f(p)为采样函数,v为采样点。因采样密度比较稀疏,从Q中拟合出的隐式等值面S与真实等值面S0之间必定存在较大差异,也就是S与S0之间的豪斯托夫距离过大,而这也在很大程度上影响了三维重建效果。取变形函数:
ω:Q→Q′
(4)
在通过变形函数的转换后,得到新的体数据集Q′,而Q′中的等值面为:
S′={v′|f′(v′)=T}
(5)
其中
(6)
从上述公式可以看出,函数ω是体数据变形的重点所在,也是本文的研究重点。函数ω必须使得从Q′中拟合的等值面S′与真实等值面S0之间差异减小,同时Q′能够满足前面所说的两个条件。
本文中采用了改变体数据中感兴趣区域内体素的顶点位置来实现体数据变形,其中顶点的位移量最为关键,它直接影响到函数ω的变形效果,它的计算是根据顶点的相邻点位置及采样值得出。为了解决因为体素顶点的位移量相对显示尺寸非常小, 导致单次位移的效果并不明显的问题,本文采用了对采样点进行多次迭代位移的方法。迭代的结束通过在每次迭代过程中发生的位移量被累加,直到总位移量S达到设置值停止迭代或是设定迭代次数的上限。
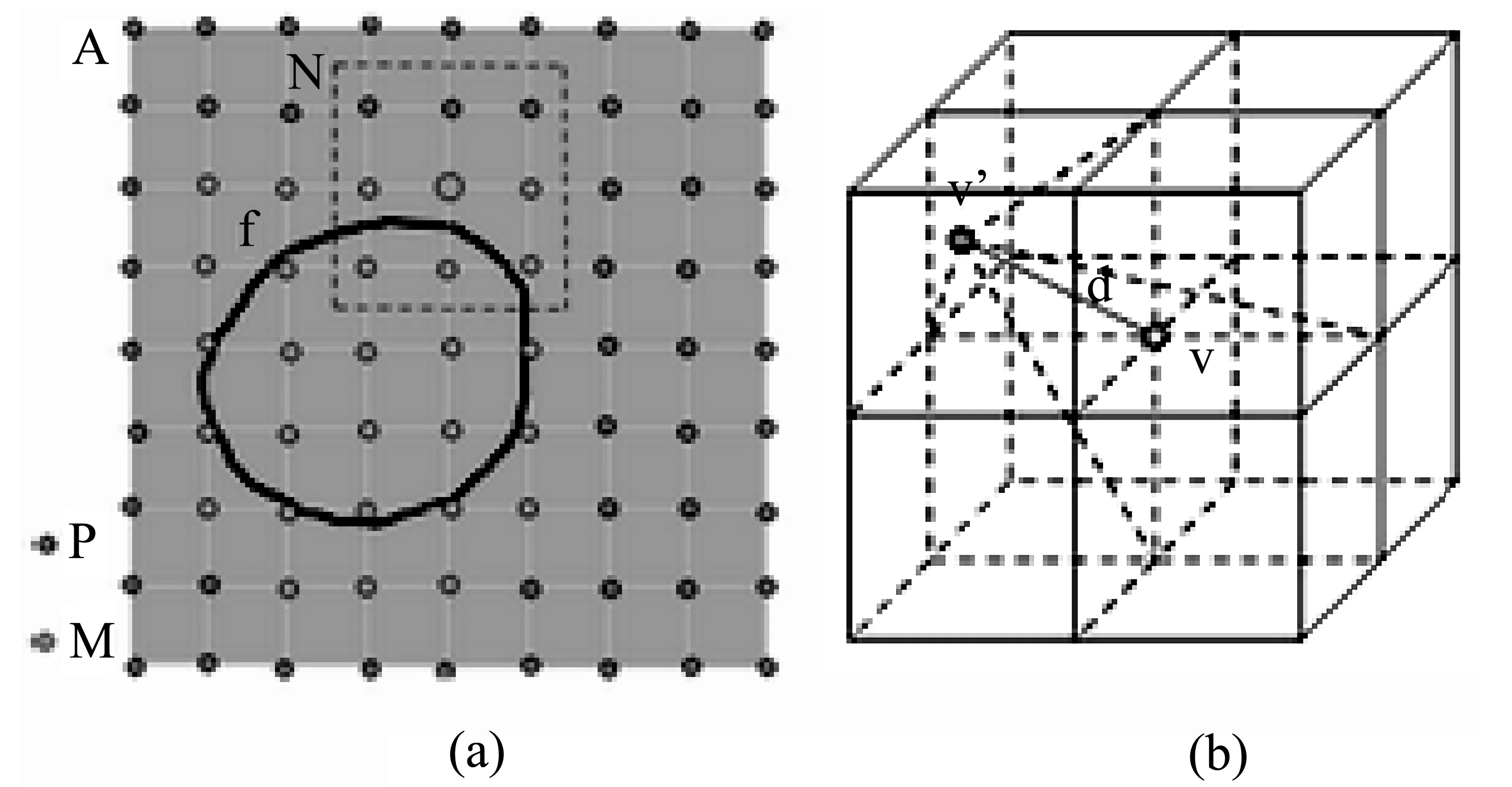
图1 体素顶点位移
如图1(a)所示,A是三维体数据中的某一层,W是A中的采样点集合,P是A中感兴趣区域外的采样点集合(即无关体素的顶点),M是A中感兴趣区域内的采样点集合,f(vi)是顶点vi∈M的值。vi的26个邻点组成集合Ni,其中ni,j是vi的第j个邻点。
W={wi|wi∈A}
(7)
P={pi|pi∈λA}
(8)
M=W-P
(9)
Ni={ni,j|ni,j是vi的第j个邻点}
(10)
变形的过程是通过迭代的方式完成,在每次迭代中,体数据中vi的位置都会发生矢量大小为di的位移,如图1(b)所示。因为单次位移量相对显示尺寸非常小,所以迭代的次数越多,重建的精确度也就越好,当迭代次数达到一定量时,改善效果不再出现明显提升。顶点vi在经过n次迭代位移后,它的位置为
,2,…,N
(11)
采样点的位移矢量di的计算与采样点的26个邻点ni,j的坐标及采样值有关,公式如下
(12)
其中
(13)
μi是点vi的26个邻点采样值的总和,μij是计算位移矢量di时每个邻点相应的权重。由公式(12)可以看出,位移矢量di的计算与采样函数无关,即体数据是否归一化对di的计算没有影响。
本算法中为了保证在变形过程中体数据本来的拓扑结构不变,对位移矢量di采用了一个约束条件,限制了位移量的大小,避免因为位移量过大而导致体素拓扑结构的改变,如公式14所示
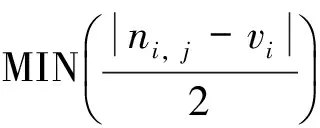
(14)
通过变形得到Q′后,根据公式6-7可以看出,要得出新的拟合等值面S′必须计算出Q′中的采样函数f′和函数η。在Q中取一个采样点V,其值和空间位置为别为f(v)和v,经过变形后V在Q′中的值和空间位置为f′(v′)和v′ 。要计算出f′(v′)则必须先确定v′在Q中所属的体素C,也就是得出函数η,可以通过v′的坐标值得出。对三维数据场中空间上的任意一点,都可以通过对该点所属体素的八个顶点使用三线性插值公式得出其值,因此,最后f′(v′)可以由体素C的八个顶点的采样值来插值估算。三线性插值公式如下
F(x,y,z)=(1-x)(1-y)(1-z)F(0,0,0)+
(1-x)(1-y)zF(0,0,1)+(1-x)y(1-z)
F(0,1,0)+x(1-y)(1-z)F(1,0,0)+
(1-x)yzF(0,1,1)+xy(1-z)F(1,1,0)+
x(1-y)zF(1,0,1)+xyzF(1,1,1)
(15)
经过化简可得
F(x,y,z)=axyz+bxy+cyz+dzx+
ex+fy+gz+h
(16)
其中F(i,j,k)为体素C顶点的采样值,a,b,c,d,e,f,g,h为常数,由体素C的八个顶点值唯一决定。
2.3 算法实现步骤
本文所提出的算法步骤如下:
1) 采用了区域生长法对体数据进行分割,具体流程如2.1中所述;
2) 设定迭代结束的条件位移总量S0或迭代次数L0;
3) 遍历分割后的体数据集Q,对每个体素的顶点进行位移,同时位移量与总位移量S相加;
4) 完成当次遍历后,当前迭代次数L加1,同时判断是否达到迭代停止条件,如果没有,继续步骤3;
5) 结束体数据变形,对体数据集Q′进行三维重建,抽取等值面S′。
3 算法优化及并行运算
本文中的采样点位移矢量是根据体数据空间中采样点的邻点计算得出,而在计算过程中由于遍历的顺序不同,采样点的邻点或先于或后于采样点发生了位移,邻点的变化也影响着采样点位移矢量的计算,也就是说计算顺序的不同,对计算的结果有着一定程度影响。但是,由于本算法是一个对体数据中所有点进行多次迭代运算的过程,在一次迭代中因计算先后关系所产生的邻点变化,相对于整个运算过程,对采样点位移矢量计算的影响可以忽略不计。设定在每次迭代过程中,计算采样点的位移矢量时,所用的邻点的状态(位置和采样值)都取上一次迭代后的计算结果,因此,在每次迭代过程中,对每个采样点的位移计算都是一个独立单元,可以使用多线程访问共享内存的方式进行并行运算,这样可以很好的提高了算法的运算效率和运算速度。
本文中算法的并行实现是基于CUDA平台[7]。在CUDA的架构中,CPU和GPU是协同工作的,并不是只有GPU在工作,其中CPU负责处理逻辑性较强的事务以及串行计算,而GPU则主要专注于并行处理任务。因此在CUDA的编程模型中,总是需要给CPU和GPU进行分工。在算法实现的过程中CPU部分的主要工作是:确定kernel线程的组织方式;将体数据读入并传入显存;分配必要的内存空间以及通过循环迭代方式调用Kernel函数。在CPU完成必要的准备工作后,就可以执行kernel函数了。本算法中kernel主要是负责顶点位移计算的部分,大致可分为三个步骤:计算位移后的顶点的空间位置;计算位移后的顶点的数值(即灰度值);更新存放位移变形后体数据的数组。在上述kernel函数里的三个步骤,是由线程串行执行下来的,而在GPU中同时有多个线程在并发执行kernel函数,因此算法的运算速度相较CPU上提升十分明显。
4 实验结果及分析
采用开发工具VS2005与OpenGL实现本文提出的算法,在实验中选取的数据集是一组球体数据(sphere)与头骨CT数据(skull),数据的规模分别是32×32×32和64×64×64,点距分别为0.556 mm和0.435 mm,对两组体数据使用传统移动立方体算法和本文的算法进行三维重建。对于重建后等值面的精确度,可以通过隐式等值面与真实等值面之间的Hausdorff距离来衡量。如图2所示,对于两组数据集,采用本文中算法得出的Hausdorff距离比传统移动立方体算法的距离明显要小,并且随着迭代次数的增加,Hausdorff距离越来越小,当迭代达到一定次数时,Hausdorff距离不再明显变化。
从图3可以看出,使用传统移动立方体算法重建的三维球体模型表面存在很多凹凸,存在着成像效果不好,精确度不高的问题。与之相比,用本文中的算法重建的模型表面更为平滑逼真,同时,可以看出随着迭代次数的增多,模型的精确度也越高。

图2 两种算法的Hausdorff距离

图3 球体重建对比图
与传统移动立方体算法重建出的三维模型比较,使用本文算法在显示效果上大体一致,但在精确度方面有所提高。如图4所示,头骨右上的凹陷部分在图4(a)中的显示效果略显模糊,绘制出的网格出现重叠;从图4(b)可以明显看出在使用本文算法进行体数据处理后(迭代次数为100次),绘制的精确度大大提高,对于凹陷部分的显示效果增强,有助于用户对局部细节有着更精确的了解。
如表1所示,对于同样的体数据集,与John提出的同样基于体数据变形的自适应算法相比[6],本算法在经过体数据分割后,所需要计算的顶点数量明显减少,算法的效率也随之提高。
接下来在CUDA平台上实现算法加速,硬件配置为:Core 2 T6600处理器,2 GB DDR3内存,NVIDIA Geforce GT 130M(512MB)显卡。如表2所示,经过算法优化后的并行加速,与John的自适应算法[6]相比或是与在CPU上直接实现本文算法相比,运算速度有着大幅度提升,提升大约为20倍左右,这也保证了在应用过程中,本算法能够满足用户实时性的要求。同时,随着硬件性能的提升,本算法的并行加速效果会越明显。

表1 顶点数量的比较(迭代次数均为1)
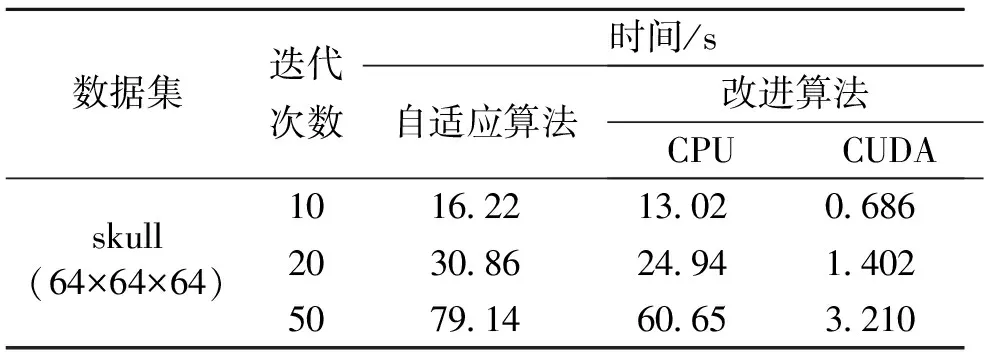
表2 算法速度对比
5 结 论
为了解决三维重建过程中,对于采样稀疏的体数据移动立方体算法并不能满足所需精确度要求的问题,本文提出了一种基于体数据变形的自适应移动立方体算法。采用本算法对密度稀疏的三维数据场进行三维重建,体数据会发生自适应形变,感兴趣区域内的采样点密度得到提高,体素内所包含的三角面片更加逼近等值面,同时并未增加采样点的数量。因此相比采用增加采样点策略的改进算法,在进行等值面绘制时本算法在运算效率上更为优越。
为了进一步提高算法效率,本文采用交互式区域生长法对体数据进行分割,并且还使用CUDA对算法进行并行加速,这样既避免了在体数据变形过程中对感兴趣区域外采样点的无关运算,又可以在三维重建过程中提供较好的实时性与交互性。下一步的研究工作是在对大体数据进行三维重建后,进行局部放大时如何保证图像效果的精确度。
参考文献:
[1]伍国永,罗月童.体数据的高质量可视化[C]//全国第21届计算机技术与应用学术会议,2010: 32-35.
[2]LORENSEN W E,CLINE H E.Marching cubes: a high resolution 3D surface construction algorithm [J].Computer Graphics,1987,21(4): 163-169.
[3]WEBER G H,KREYLOS O,LIGOCKI T J.Extraction of crack-free isosurfaces from adaptive mesh refinement data [C]// Data Visualization 2001,2001: 25-34.
[4]YING B,XIAO H,JERRY L P.Octree grid topology preserving geometric deformable model for three-dimensional medical image segmentation [J].Computer Science,2007,4584: 556-568.
[5]PAIVA A,LOPES H.Robust adaptive meshes for implicit surfaces [C]// SIBGRAPI’06,2006: 205-212.
[6]CONGOTE J,AITOR M,OSCAR R.Extending marching cubes with adaptive methods to obtain more accurate iso-surfaces [J].Communications in Computer and Information Science,2010,68(2): 35-44.
[7]NVIDIA CUDA programming guide 1.0 [EB/OL].http://www.nvidia.com/object/cuda_Develop.html.
[8]TIMOTHY S N,HONG Y.A survey of the marching cubes algorithm [J].Computers & Graphics,2006,30: 854-879.
[9]TIAN J,XUE J,DAI Y K.A novel software platform for medical image processing and analyzing [J].IEEE Transactions on Information Technology in Biomedicine,2008,12(6): 800-812.
[10]ADAMS R,LEANNE B.Correspondence seeded region growing [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1994,16(6): 641-647.
[11]LONG C J,ZHAO J H,RAVINDRA S G.A new region growing algorithm for triangular mesh recovery from scattered 3D points [J].Transactions on Edutainment VI,2011,6758: 237-246.

