基于扭摆的力学谱仪在强迫振动模式下的延时误差分析*

杨岳彬，左文龙，保延翔，刘树郁，李龙飞，熊小敏

(1.中山大学信息科学与技术学院，广东 广州 510006;2.中山大学光电材料与技术国家重点实验室∥广东省光伏技术重点实验室∥物理科学与工程技术学院 广东 广州 510275;3.中山大学东校区教学实验中心 广东 广州 510006)

内耗是表征固体机械能损耗的物理量，内耗与固体中的微结构，如：相界、位错、空位的性质及其演化等有重要联系[1]。基于扭摆的内耗仪即葛氏扭摆[2]是目前低频内耗测量中重要的实验手段，近年来被广泛应用于合金马氏体相变[3-5]、缺陷运动[6-8]等研究领域。近年来扭摆型内耗仪在经过改进后也可以实现对流体黏弹性行为的测量，因此发展成为了集固体内耗测量、流体黏弹性测量为一体的力学谱测量仪器。

扭摆型内耗仪的工作模式分为自由衰减和强迫振动两种，在实际内耗测量中人们发现：虽然强迫振动法具有可以实现连续变频测量的优点，但强迫振动法的测量精度远低于自由衰减法，利用强迫振动法测量得到的内耗值往往比自由衰减法测量得到的结果偏大。在进行流体黏弹性测量中，我们也发现测量结果计算出的黏度与理论值总是存在2-3%左右的系统误差。

本文分析、讨论了扭摆型内耗仪在强迫振动法测量内耗时的系统误差，发现误差主要是由测量系统中电路延时及机械延时导致的。在此基础上我们提出了测量系统总延时的实验方法，同时使用测量得到的系统延时对扭摆型力学谱仪在强迫振动模式下的测量结果进行了修正，从而使之在强迫振动模式下可测量得到更为精确的固体内耗值及液体黏度值。

1 基于扭摆的强迫振动法测量固体内耗时主要误差分析

我们首先利用倒扭摆内耗仪讨论在强迫振动模式下测量内耗时的主要误差来源。

倒扭摆内耗测量仪结构如图 1 (a)所示，其中1为摆杆，2为底座及支架，3为固体试样，4为悬线及扭丝，5为电磁线圈，6为永磁铁，7为反射镜，8为螺杆，9为附加配重砝码(3组)，10为光源，11为二象限光电池。

图1 倒扭摆内耗测量仪示意图

当电磁线圈中通过交变电流时，将会产生交变磁场，使摆杆作同频率的强迫振动。这时，摆杆的运动方程如下

(1)

(2)

如果测量得到各个频率下应变落后于应力的相位差以及系统的共振频率，就可以根据(2)式得到样品的内耗-频率谱。我们测量了恒弹性合金的内耗-频率谱如图 2所示，内耗-频率谱上出现了一个很宽的内耗峰，更换其它样品如：铜，钛等，都在相近的频率存在类似的内耗峰，这表明，图 2中的内耗峰不是样品本身的性质，而是由于测量系统引起的系统误差。

图2 强迫振动法测量得到的内耗—频率谱

从交变应力的施加方法看，应力是通过具有一定的长度(约60 cm)的摆杆传递到样品上的，该过程需要用扭转振动的波动方程进行严格描述。当利用强迫振动法进行内耗测量时，由于忽略了扭转振动在摆杆上的传播所需要的时间，使得在实际测量应变落后于应力的相位差时引入了系统误差。

另一方面，从应变的测量方法看，摆杆扭转的角位移是通过如图 1 (b)所示的光杠杆法进行测量的。摆杆扭转时，光斑在左右两块光电池上的分布发生变化，进而产生交变电流信号。为了对这一应变信号进行放大以进行检测分析，同时保证电路拥有非常低的噪声以及失真度，我们使用了如图 3 (a)所示的电路。其中，引入电容CF使电路保持稳定，电阻RF则决定了电路的增益。

上述电路可以等效为一个有源二阶巴特沃斯低通滤波器。电路的等效模型如图3(b)所示[9]。该电路的相位特性如下[10]

图 3 应变信号测量电路

(4)

式中α表示滤波器的阻尼比，其值为滤波器Q值的倒数，ω0=2πfb为截止角频率，ω为系统当前工作的角频率。

由(4)式可以看出，电路的延时表达式是非线性的，由α及ω0共同决定。而且，实际中，往往无法精确标定光电池的结电容和内阻，因此从电路角度精确标定(4)式引起的相位偏差几乎是不可能的。

综上所述，在扭摆的谐振子模型中，机械波传播所带来的延时和应变测量电路的延时是测量应变落后于应力相位差的系统误差的主要来源。并且随着测量频率的增大，延时对相位差测量的影响会越发严重，导致相位差的误差增大。基于扭摆的内耗仪在测量相位差时都采用了类似的模式，因此同样受到了系统延时误差的影响。这使得内耗仪无法在较高的频率下进行准确的测量。

2 扭摆系统延时的测量原理及其实现

考虑扭摆型内耗仪在另一种模式——自由衰减模式下进行内耗测量时，是通过测量衰减波形幅值的变化得到样品内耗的。这一过程并不涉及到波形的相位测量，因而上述系统延时不影响自由衰减的测量结果。

我们提出如下的测量系统延时的方法：首先通过自由衰减法测量得到样品在自由衰减频率ω下的内耗精确值为tanφ，考虑强迫振动的共振频率为ω0，则在频率ω进行强迫振动测量时应变落后于应力下相位差δ应该满足：

(5)

若这时通过频率为ω的强迫振动测量得到的应变与应力的相位差为δ′，则δ′-δ即为由系统延时引起的误差。假设这时系统延时为τ，考虑到测量频率为ω，则由系统延时引起的强迫振动相位差测量误差为ωτ，由此我们可以计算出系统的延时τ：

(6)

为了使自由衰减的频率ω与强迫振动测量时的系统共振频率ω0不至于太接近，并且让系统可以在不同的多个频率下进行自由衰减测量，我们设计了一种可以在保持样品状态不变的情况下改变系统转动惯量的装置如图 1 (c)。装置包括摆杆上增加的一个垂直于摆杆轴线的螺杆，以及与之相配的三组配重砝码(图中只画出一组)，每组砝码可以旋紧固定在摆杆中加入的螺杆上，以改变系统的转动惯量，从而实现了进行不同频率下自由衰减测量。

根据上述的方法，利用三组不同的配重对三个频率下的延时进行测量：其中自由衰减分别在三组不同的配重下进行测量，相应的得到了三个不同频率，53.21 Hz，45.72 Hz以39.36 Hz及 下的样品内耗，之后在没有附加配重的条件下测量得到了系统的共振频率为70.53 Hz并在频率53.21 Hz，45.72 Hz以及39.36 Hz下测量了强迫振动的相位差。可以计算出相应不同频率下的系统延时如表 1所示。

表1 不同频率下的内耗及延时

3 修正强迫振动法测量时延时产生的系统误差

3.1 修正强迫振动法测量固体内耗的误差

根据上述方法测量得到的不同频率下的系统延时后，即可对采用强迫振动测量内耗的方法进行修正。在强迫振动模式下测量得到不同频率下的相位差δ′(ω)后，使用之前测量得到的不同频率下的系统3延时通过插值法获得相应频率下的系统延时τ(ω)，并根据δ=δ′-ωτ相位差的测量结果进行了修正，并根据修正后的相位差计算得到了系统不同频率下的内耗值：

我们使用强迫振动法对金属Ti样品在30～50 Hz这一频段的内耗进行了测量，并利用之前获得的系统延时通过插值法扩展后对测量得到的相位差进行了修正。根据修正后的结果计算出样品的内耗-频率曲线，并与自由衰减测量得到的内耗比较如图 4所示。

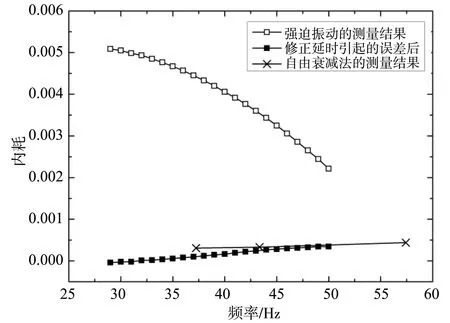
图4 强迫振动内耗经过延时修正后的结果及与自由衰减内耗的比较

从图 4中可以看出，使用延时对强迫振动的测量结果进行修正后，在很宽的频率范围内均可使强迫振动测量得到的固体样品内耗和自由衰减测量得到的内耗更接近。但对于不同的样品，由于样品长度不完全一致，机械部分造成的延时可能略有不同，这也导致经过修正后的内耗与自由衰减的测量结果之间存在偏差。综上所述，使用延时修正已经很大程度上改善了强迫振动测量法直接测量内耗绝对值的误差。本文通过测量延时，可以有效地对强迫振动的内耗测量结果进行修正，使强迫振动法也可以有效的测量出样品内耗的精确值，同时也为扭摆型内耗仪在宽频率的连续变频内耗谱的测量奠定了基础。

3.2 修正强迫振动法测量液体黏度的误差

基于扭摆的内耗仪也可以通过加装附件作为流变仪用于进行液体黏弹性测量。如图 5所示，图中1为摆杆，2为底座及支架，3为固体试样，4为悬线及扭丝，5为电磁线圈，6为永磁铁，7为反射镜，8为螺杆，9为转桶，10为盛液桶。未加入液体时，可以通过强迫振动法测量得到系统的内耗，而加入液体后，系统的损耗由固体样品的内耗和液体引起的阻尼损耗组成，这时系统的运动方程为：

(1+itanφ)θ=M0eiωt

(7)

其中ML为液体的黏滞耦合力矩，若考虑密度为ρ、黏度为η的纯黏性流体，当转桶半径为r、液体与转桶的接触面积为S、振动频率为ω时，液体对转桶产生的黏滞耦合力矩为：

·ei(ωt-δ)·ei3π/4

(8)

由此可以计算出这时应变落后于应力的相位差为：

(9)

图5 基于扭摆的流变仪示意图

如果可以准确的测量得到固体样品的内耗以及加入液体后强迫振动的相位差，即可计算出待测液体的黏度：

(10)

上述的方法可以实现对液体黏度的绝对测量，而实现绝对测量则需要实现固体内耗以及相位差准确值的测量。我们利用上述仪器对18 ℃下水的黏度进行了测量。若在测量中不考虑延时的影响，则测量得到的固体内耗和加入液体后的相位差均偏大，这时计算得到的水黏度为1.041 mPa·s，与文献报道中18 ℃下水的黏度1.056 mPa·s相差约2%。若考虑系统在测量频率下的延时，对测量得到的固体内耗和加入液体后的相位差进行修正后，计算得到的水的黏度为1.059 mPa·s，与文献报道中的值非常接近。这说明在利用这类方法进行相位差测量时，通过修正延时引起的系统误差，可以有效地提高测量的准确度。

4 结 论

本文通过分析倒扭摆内耗仪在强迫振动模式下的测量原理，指出扭摆型内耗仪强迫振动法测量误差主要来源于系统延时——包括机械波传播延时和电路延时。本文提出了测量系统延时的方法，利用测量得到的系统延时分别对强迫振动模式下固体内耗和液体黏度的测量结果进行了修正，很大程度上消除了内耗测量值的系统误差，同时使液体黏度的绝对测量误差由3%减少到1%以内。这些结果表明，通过修正系统延时误差可以有效的提高力学谱仪在强迫振动模式下的测量精度，为实现高精度的固体内耗-频率谱、流体黏弹性-频率谱的测量提供了重要的帮助。

参考文献：

[1]NOWICK A S,BERRY B S.Anelastic relaxation in crystalline solids[M].Academic Press,1972.

[2]葛庭燧.扭摆内耗仪的发明和内耗研究的开拓与发展[J].力学进展，1994(3): 336-352.

[3]李永华，王芳，郑洁，等.Ni_(49.8)Ti_(50.2)合金马氏体逆相变的瞬态内耗与频率间关系的定量分析[J].金属热处理，2008(2): 85-88.

[4]刘军民.MnCu合金热弹性马氏体相变过程中的非线性内耗行为[J].物理学报，1997(12)：1.

[5]吴青云，宫晨利，廖军.Cu-Al-Ni-Mn-Ti合金相变弛豫特性的研究[J].合肥工业大学学报：自然科学版，2008(1): 93-95.

[6]阎琦，史文，李麟，等.内耗法研究退火温度对含钒BH钢中固溶C原子浓度的影响[J].上海金属，2011(5): 10-14.

[7]张进修，陈岚，孟荟，等.BaTiO_3陶瓷中氧缺位引起的弛豫内耗峰[J].中山大学学报:自然科学版,2004，43(6)：181-182.

[8]刘文峰，李益，欧阳红群，等.Na_xCo_2O_4陶瓷的力学弛豫和阻抗弛豫研究[J].中山大学学报：自然科学版,2009，48(3)：33-36.

[9]FRANCO S.基于运算放大器和模拟集成电路的电路设计[M].刘树棠，朱茂林，荣玟，译.西安：西安交通大学出版社，2009.

[10]JUNG W.Op amp applications handbook[M].Amsterdam:Elsevier/Newnes,2006.