基于矩阵式遗传算法的集装箱码头堆场空间资源分配优化策略

顾天意，梁承姬

(上海海事大学科学研究院，上海 201306)

0 引言

堆场空间资源配置问题(Storage Space Allocation Problem，SSAP)主要是指根据堆场分类的标准和堆放原则合理确定进出口集装箱的箱区堆存数量并安排箱位.ZHANG等［1］利用滚动计划法解决进出口、中转箱的堆场空间分配问题，可大大减少堆场不平衡的工作量，有效避免码头运作过程中可能出现的瓶颈;EBRU等［2］将进口箱SSAP和场桥调度问题结合起来进行整体研究;FU等［3］考虑不同数量、大小的集装箱以及空间资源分配在计划期不同时间内的变动，研究SSAP，运用禁忌搜索算法、模拟退火算法、遗传算法(Genetic Algorithm，GA)和“squeaky wheel”优化算法求解模型;王斌［4］应用数学规划的方法求解分配到各箱区贝位的箱数，进而用线性规划法求解一个周期内每艘船要分配到各箱区贝位的箱数，降低集卡从堆场到码头前沿的行走距离，提高堆场的操作效率;李建忠等［5］在滚动计划的基础上建立集装箱堆场空间资源动态配置模型，使集卡行驶距离减少20%左右，集卡使用效率得到很大提高;陈庆伟［6］以贝位为对象，根据混合堆存策略，考虑不断变化的堆存状态和操作难度，为每一个动态到达的出口箱安排位置，以便使装船作业期间前方堆场取箱时的倒箱次数最少;陶经辉等［7］建立进出口箱堆存的数学模型，解决集装箱工作量平衡问题及箱组间平衡优化问题，用启发式算法求解数学模型，并用深圳蛇口集装箱码头实际数据仿真验证模型;白治江等［8］建立堆存空间分配的线性整数规划模型，并用滚动规划的方法解决堆场存储空间的分配方案，结果表明，模型求解时间短，能有效降低堆场中的负载不平衡问题;白治江［9］将集装箱存放空间的分配决策从逻辑上分解为箱区分配、集卡指派和箱位分配等3个目标一致的子决策，其目标是使设备空闲时间最少、翻箱总数最少、道路拥堵程度最低;严伟等［10］以降低存放处到泊位的水平运输距离和平衡堆场内作业量为目标，达到提高装船效率和降低成本的要求，建立滚动式计划的出口集装箱堆场分配模型.

本文提出用矩阵式遗传算法(Matrix Genetic Algorithm，M－GA)求解基于作业面的堆场空间资源分配模型，并在模型中综合考虑场桥因素，重点在于应用矩阵式编码方式，使GA可以迅速求得可行解.

1 问题描述

船舶依次进港并带来集装箱的箱流.每艘船都在指定的时间到港，并且已经确定将要卸船和装船的集装箱箱量.本文在计算集装箱数量时区分进口箱和出口箱，并始终使用TEU作为数量单位.船期直接确定进口箱的到达时间和出口箱的离开时间.因此，可以提前确定对这两种类型集装箱的作业(用龙门吊和岸桥)时段.

堆场空间资源分配的施行就是在基于作业路考虑集装箱整体运输距离的基础上，平衡各个场桥的工作量，预计各个计划时段进入堆场的集装箱并完成箱区分配.本文所研究的堆存问题的规模由作业路数、箱区数量以及场桥数量共同决定，港口实体布局示意图见图1.

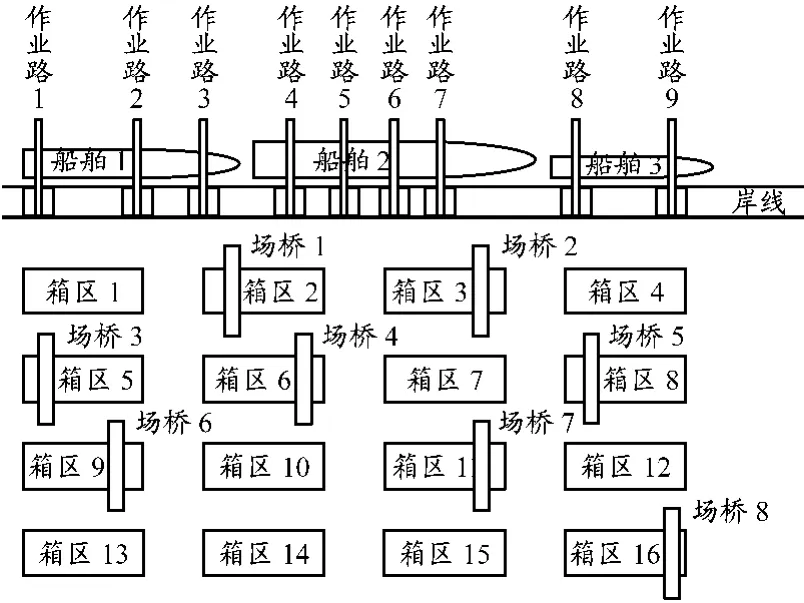
图1 港口实体布局示意图

考虑到船舶的大型化趋势，大型集装箱港口在对船舶作业时采用多条作业路的并行作业方式.因此，应用基于作业路的堆场空间分配策略，实现并优化堆存方案.

港口堆场中90%的堆存安排工作量来自等待进场的集装箱，仅仅是在倒箱和整理堆场时会对出口箱做堆存安排.因此，重点研究进口集装箱.

对于确定的船舶和计划时段，集装箱的信息是已知的.因此，只要给定该船的装卸量，就可以推断出其在任意时段内的作业量.通过岸桥的分配，可以确定船只的作业路数及各条作业路的工作箱量.因此，本文针对一个特定的作业时段研究进口箱的分配方案.对于整个计划周期，在每个时段只要循环使用分配策略就可求得该时段的堆存方案.

对于场桥，跨行作业所需的运行时间要比同行作业大得多，因此在场桥不跨行作业的基础上求解堆存方案，即某一行箱区的可用场桥只是当前作业时段开始时刻已经在该行的场桥.例如，图1中箱区1，2，3和4的可用场桥为场桥1和2.根据测算，场桥的起升频率是50次/h.因而，可以计算得到每个场桥在某个作业时段内的最大工作量.

2 基于作业路的堆场空间资源动态配置数学模型建立

2.1 相关假设

某一天内所有靠港船舶的停靠泊位和卸载进口箱量已知;该天每艘船开通的作业路数及各作业路的任务量已知;堆场拥有足够的内集卡，且内集卡、场桥每次只处理一个集装箱;不考虑集装箱的箱型和重量，所处理的集装箱尺码统一为20英尺.

2.2 模型建立

2.2.1 参数定义

B为堆场的箱区总数;V为一天内要卸货的船数;l为船的作业路数;i为箱区序号;j为船舶序号;p为作业路序号;Ci为箱区i的可用空间(每个集装箱占用一个空间);Ejp为船舶j第p条作业路卸载的进口箱堆存的最多箱区数;Yjp为船舶j第p条作业路卸载的进口箱量;dij为箱区i与船舶j停靠泊位间的距离;Xij为箱区i堆放船舶j的进口箱量;M为一个大数.

2.2.2 决策变量

Xijp为箱区i堆放船舶j第p条作业路卸载的进口箱量;当Sijp=1时，表示箱区i堆存船舶j第p条作业路卸载的进口箱;当Sijp=0时，表示箱区i未堆存船舶j第p条作业路卸载的进口箱.

2.2.3 目标函数及约束条件

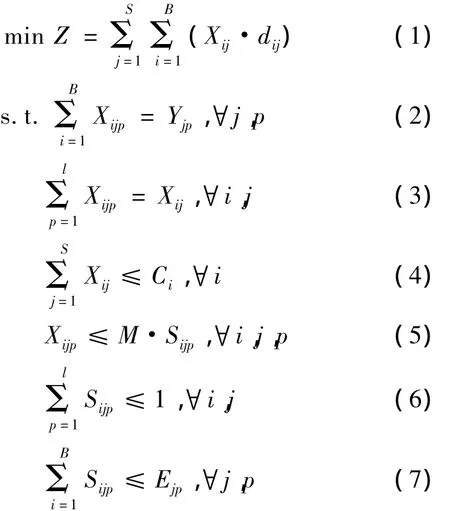
目标函数(1)表示船舶j的进口箱的卸箱总距离最小.约束(2)表示船舶j第p条作业路卸下的进口箱量等于分散在各堆存箱区的箱量之和;约束(3)表示箱区 i堆存的船舶j进口箱量等于该船各条作业路卸至该箱区箱量之和;约束(4)表示箱区i堆放的所有船的进口箱总数小于其容量;约束(5)用于判断箱区i是否已堆放船舶j第p条作业路卸载的进口箱;约束(6)表示箱区i只能堆放船舶j一条作业路的进口箱，或者不堆放船舶j的进口箱;约束(7)表示船舶j第p条作业路卸载的进口箱堆放的箱区数小于给定的最多箱区数.

3 M－GA 的实现

GA实现最重要的一步是解的表示，也就是对染色体的设计.因此，为了快速找到可行解，并高效搜索到最优解附近，本文运用M－GA［11］求解堆存问题.

3.1 基于矩阵的染色体设计

3.1.1 编码

以矩阵构造满足系统约束条件的某一堆存计划的染色体，第p个染色体矩阵为

3.1.2 生成初始解群

生成初始解的步骤为

步骤1判断作业路是否全部遍历:是则初始解构造完毕;否则选择一个作业路i.

步骤2任选2个箱区1和2，判断箱区剩余容量之和是否大于所选作业路的需求:是则进入步骤3;否则重做步骤2.

步骤3比较作业路i的需求与箱区1的容量:若箱区容量大于作业路需求，则将作业路i的需求全部分配给箱区1;若作业路i分配给箱区1的箱量等于箱区1的容量，则作业路i分配给箱区2的箱量等于作业路i的需求减去箱区1的容量.

步骤4重新计算箱区1和2的容量.

步骤5遍历任选2个箱区的所有组合:对于作业路i+1，若满足所有条件，进入步骤(1)再生成;若没有任何组合的容量和大于需求，则重新构造.

3.2 M-GA设计

3.2.1 交叉算法

步骤1由父代染色体X1和X2组成两个矩阵D=(dij)和R=(rij).

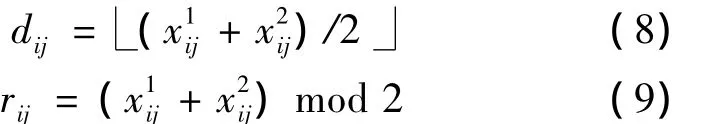
步骤2将矩阵R分解为R1=()和R2=)，R=R1+R2.

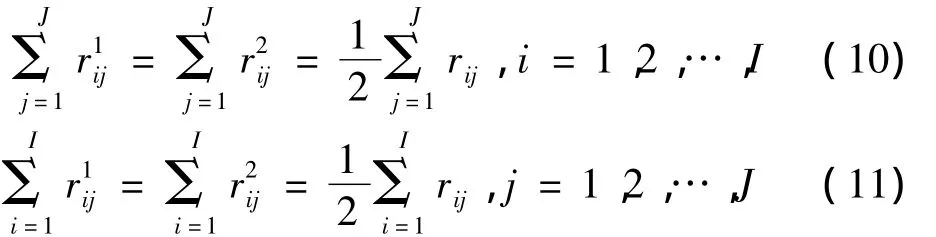
步骤3生成两个子染色体X'1，X'2.

3.2.2 变异算法

步骤1根据父染色体矩阵构造子矩阵.随机选取行{i1，i2，…，ip}和列{j1，j2，…，jq}，生成(p·q)型的子矩阵Y=(ykl).

步骤2重新分配子矩阵的元素.被重新分配的元素总和

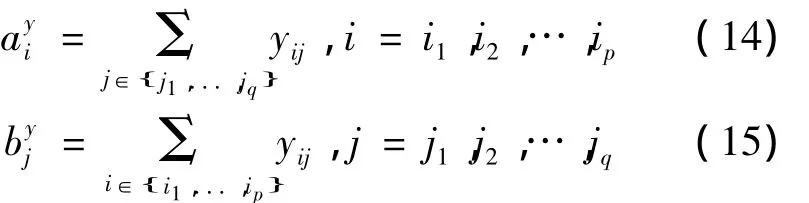
步骤3将重新分配的子矩阵Y放回父染色体矩阵原来的位置，从而生成新染色体.

3.3 父代选择策略

采用轮盘赌方式产生与种群相同数量的染色体即为下一代.

3.4 结束规则

如果迭代到最大一代(Gmax)，则停止;否则进入下一代，转第3.2节.

4 算例与结果分析

首先利用上海张华浜码头的案例验证本文所建模型和GA的有效性，并分析所提出的M－GA的性能，然后比较M－GA与传统求解方法的优劣.

为了更好地理解和验证本文所提出模型的准确性，针对该实际案例在模型中忽略靠泊时间.本次试验计算得出一个计划周期内的一个时段的堆存方案，在现实中将其多次循环，就能得到整个计划周期的堆存方案.

4.1 输入参数

所研究的堆存问题的规模由作业路数、箱区数量以及场桥数量共同决定.算例初始参数的示例见表1～4.

4.2 结果分析

4.2.1 M－GA策略比较分析

4.2.1.1 初始解群分析

通过研究发现，初始解群的构成对M－GA的搜索效率有很大影响.最初，使用纯左上角法构成解群，结果不令人满意，算法需要搜索25万代才能到达最优解附近;然后，在生成初始解群的算法中加入相类似的左下角法、右上角法以及右下角法，并用随机选取的方式确定初始解群中某个解的生成方法，之后算法的收敛速度有所增加，但还是要在10万代左右才达到收敛;之后，又在初始解群中加入一半的随机解来满足解群的多样性需求，这样生成初始解的策略可大大提高算法的搜索效率，在1万代左右即可趋向收敛.M－GA收敛比较示意图见图2.

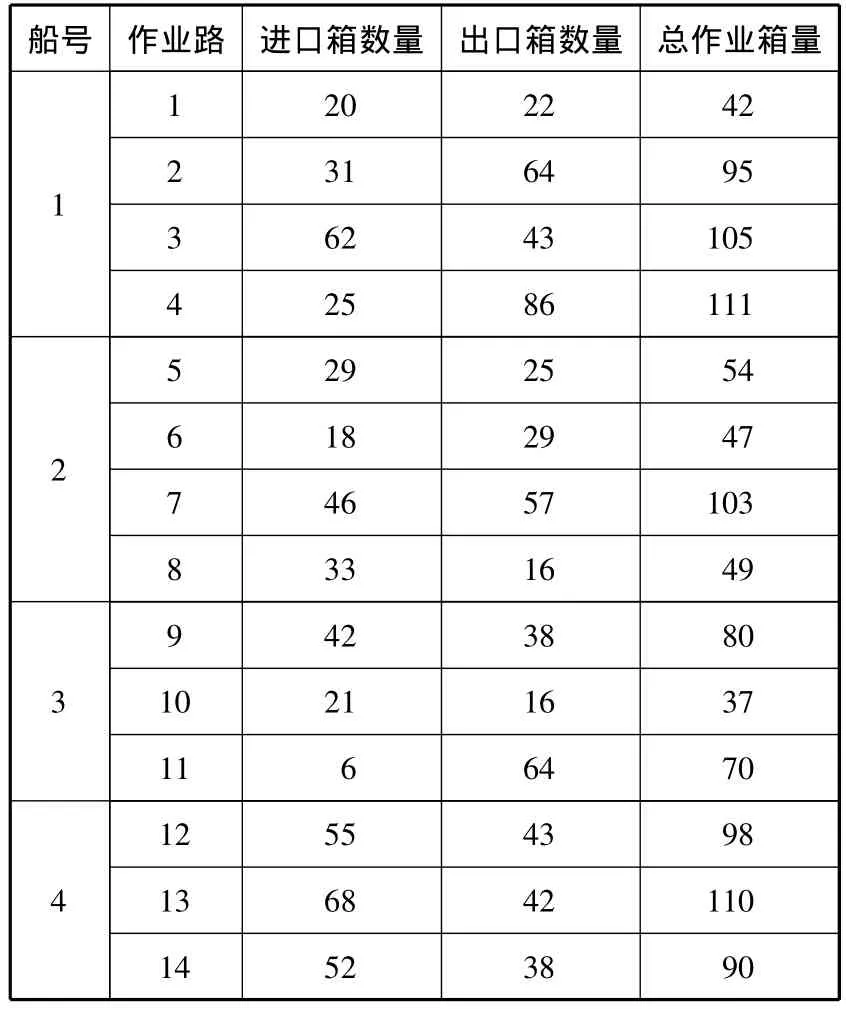
表1 计划周期内船舶的相关数据 TEU

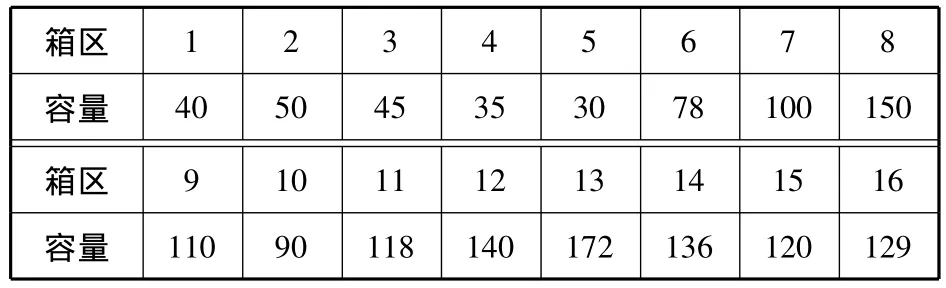
表2 当前计划时刻的堆场容量 TEU

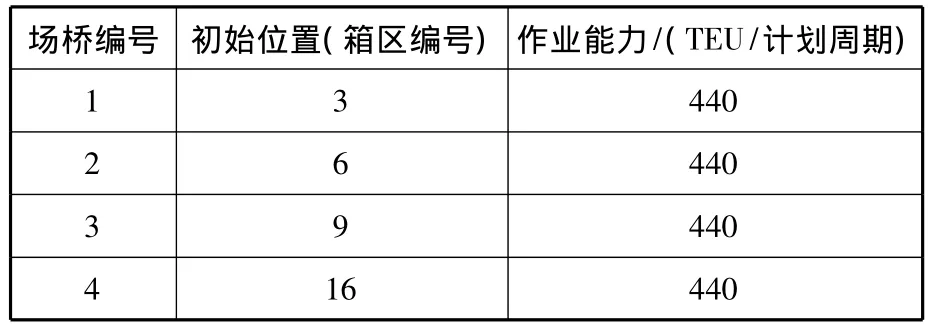
表3 计划周期内各场桥的相关信息

4.2.1.2 交叉变异算法分析

在选择交叉和变异策略时发现，不同的交叉变异策略对最终求解得出的堆存分配方案效果有很大影响.最初，选用自然交叉策略和自然变异策略，即在交叉算法中从两个父代染色体矩阵随机挑选矩阵元素做随机互换操作，构成子代染色体;在变异算法中，对父代染色体矩阵的子矩阵做随机自然数变换.计算结果表明，算法得到的最终解与最优解的误差在10%以上，堆存方案不太理想.之后，通过对矩阵结构的分析，使用第3节中所描述的交叉变异算法，得到的最终解与最优解的平均误差在4%以内.上述两种方案的堆存效果见图3～6.在堆场容量图中，上方为岸线，箱区中显示当前该堆场的使用率(填满为100%，空白为0).从图中可见，使用本文提出的交叉和变异算法后，各场桥的作业量较为平均，集装箱的堆存更为靠近岸线，运输总距离较短，更符合堆存数学模型的目标.表5中给出使用矩阵约束交叉变异算法后的计算结果.

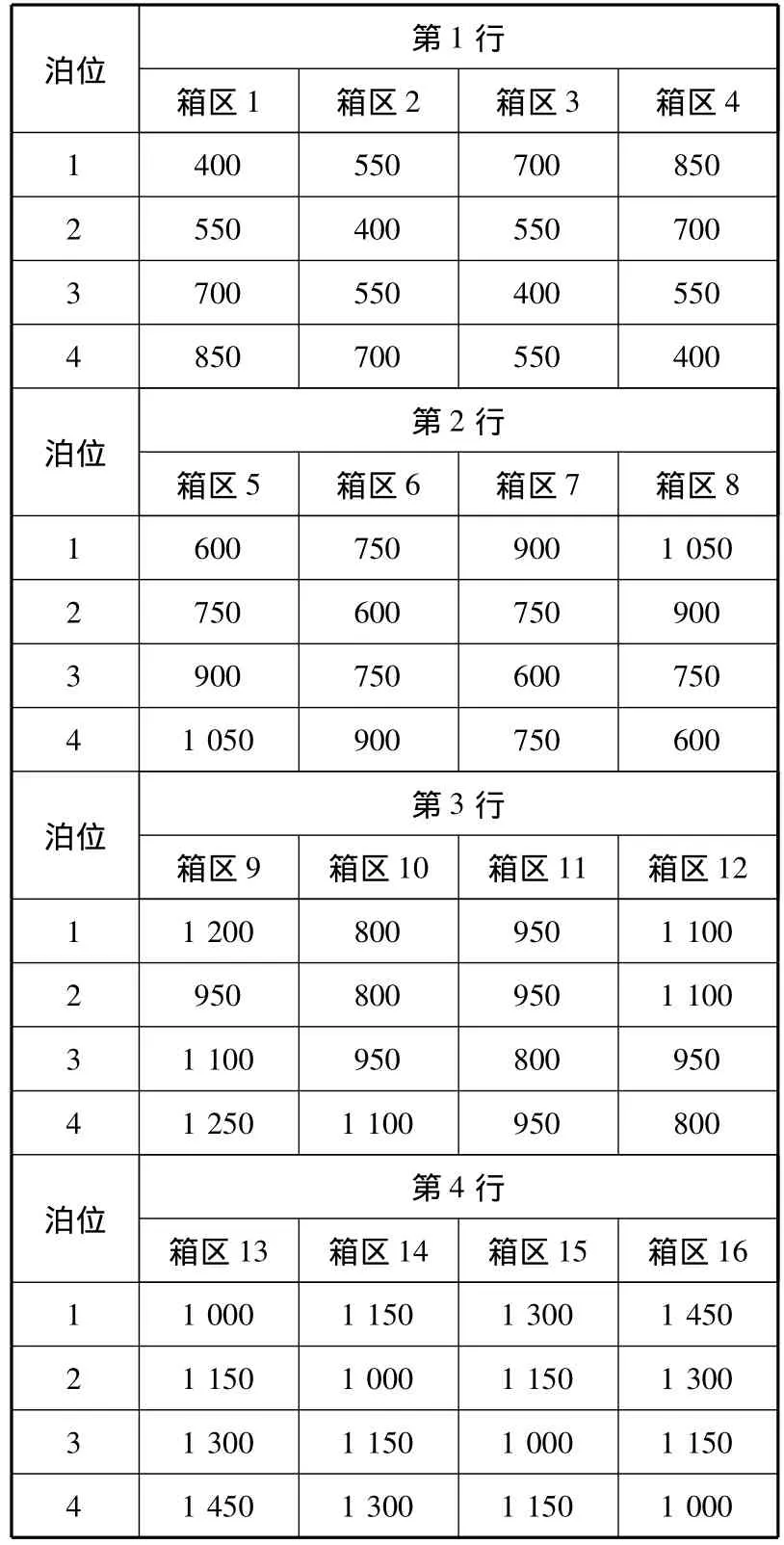
表4 箱区与泊位距离 m

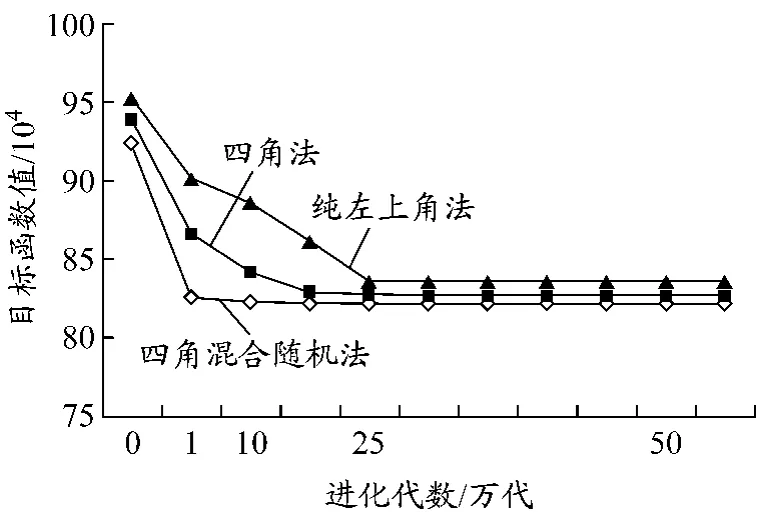
图2 M-GA收敛比较

图3 计划前堆存情况

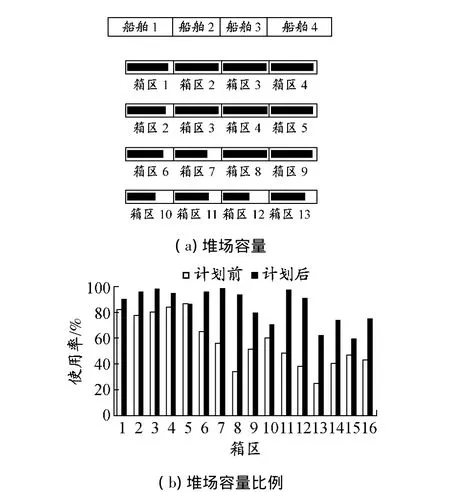
图4 计划后使用自然数变异算法后的堆存情况

4.2.2 算法优势分析

通过改变控制参数来控制问题的规模，用20个规模不同的算例比较本文所提出的M－GA和传统求解方法的优劣.对于小尺寸的案例，试验中在一台装有Intel双核P8600@2.6 GHz处理器和2 GB内存的个人电脑上，用Gurobi 400求出最优解.然而，想在合理的时间内利用规划求解的方法求解出一个大尺寸案例的最优解是不可能的.本文用M－GA求解所有案例，在合理的时间内可以得到较优值.在实验中用M－GA对每个案例都求解50次，并将M－GA目标函数值的均值与Gurobi的计算结果之间的相对误差(GAD)列于表6和7中.用Gurobi求解大型问题最优解的时间接近3 h，这些最优解也列在表6和7中.然而，超大型案例在3 h的求解以后，用规划求解的方法找不到可行解，只列出M－GA的求解结果.MGA的计算时间根据M－GA求得最优解的质量确定，在本次试验中，当M－GA趋向收敛时计算即终止.

图5 计划后使用矩阵约束交叉变异算法后的堆存情况

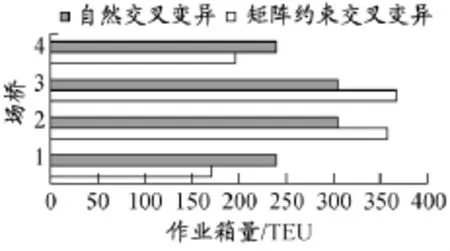
图6 场桥作业量甘特图对比

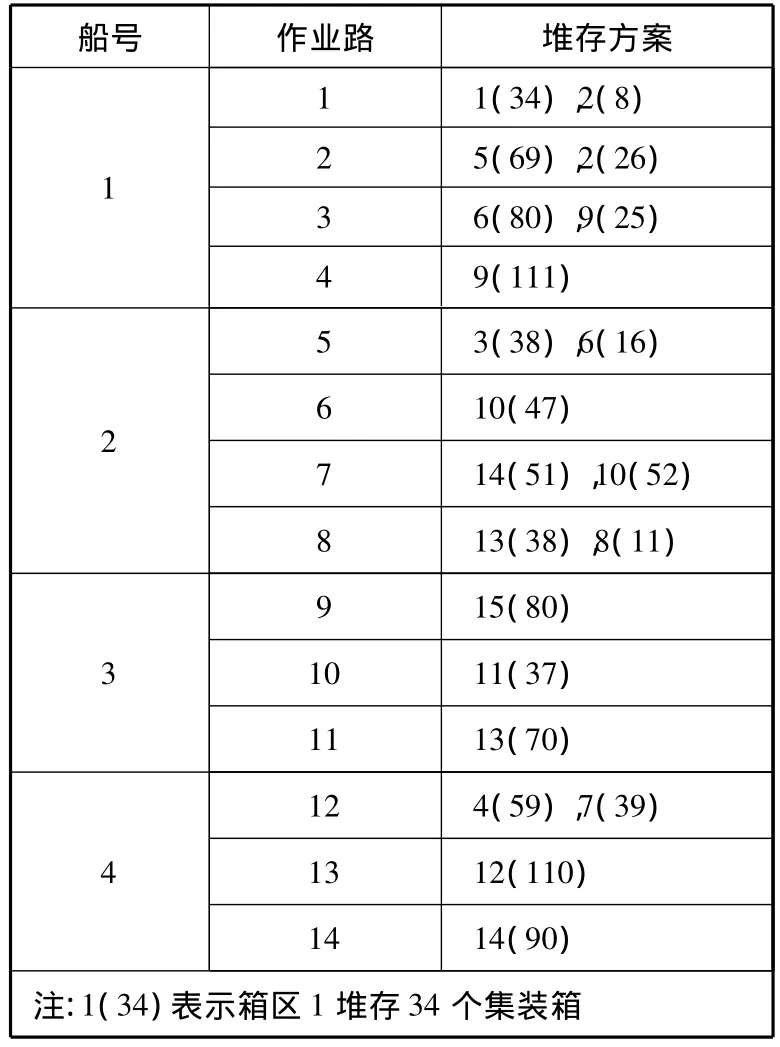
表5 矩阵约束交叉变异算法堆存分配结果

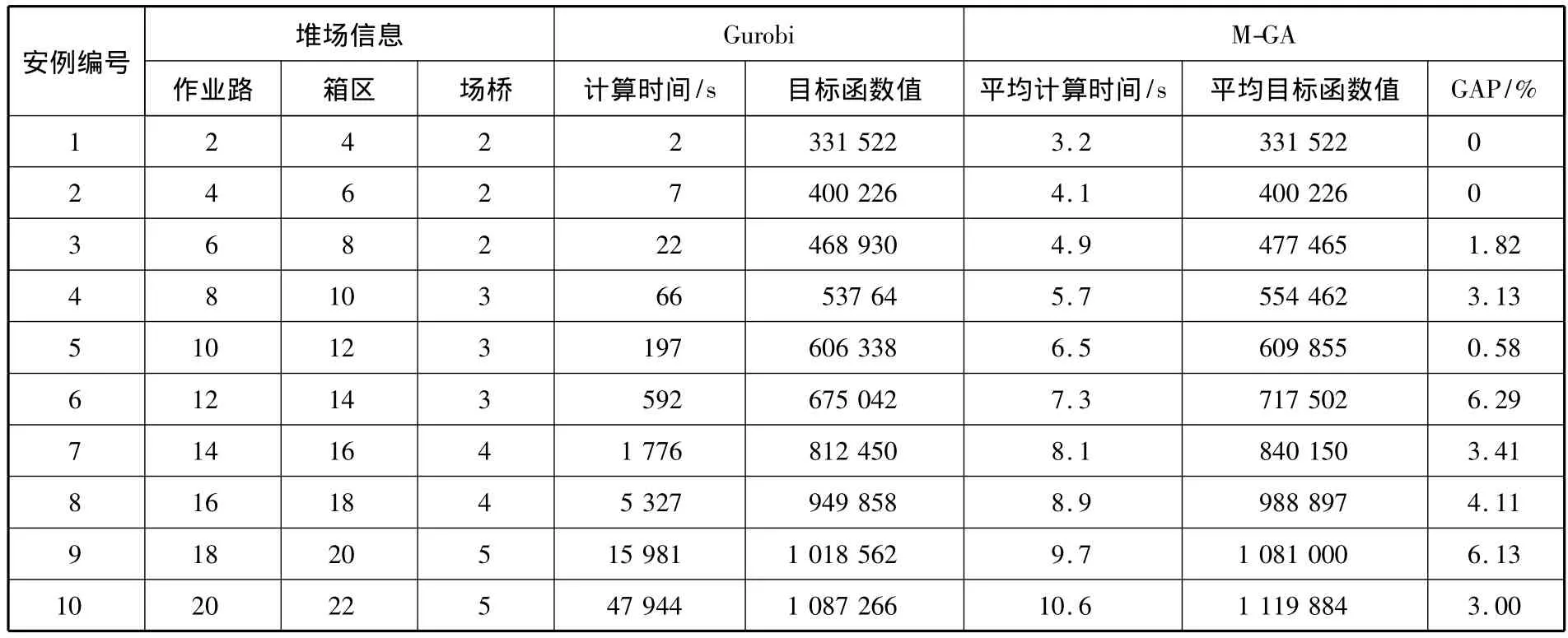
表6 小型案例最优值与M-GA值的比较

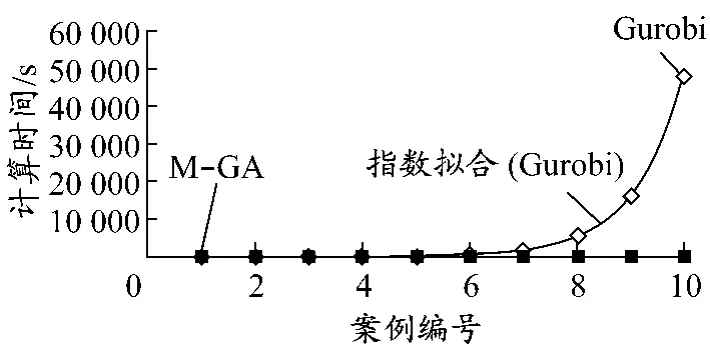
图8 Gurobi与M-GA计算时间对比

在图8中，对比M－GA与Gurobi的计算时间.可见，随着计算量的增加，Gurobi的求解时间呈指数增长，而M－GA的计算时间基本不变.

5 结束语

用M－GA解决针对集装箱港口的空间资源分配扩展问题(堆存问题).不仅考虑原有条件，也考虑场桥的初始位置及场桥的数量，使在场桥调度中各条作业路的任务都能在计划周期内完成.本文求解出一个典型案例的最优解，从而验证所提出的数学模型和M－GA的有效性.用20个不同规模的案例比较M－GA和传统求解方法的优劣，结果发现，M－GA的结果与目标函数最优值有4%左右的误差.

表7 大型案例最优值与M-GA值的比较

［1］ZHANG Chuqian，LIU Jiyin，WAN Yat－Wah.Storage space allocation in container terminals［J］.Transportation Res:Part B，2003，37(10):883－903.

［2］EBRU K，BISH.A multiple－crane－constrained scheduling problem in a container terminal［J］.Eur J Operational Res，2003，144(1):83－107.

［3］FU Z，LI Y，LIM A，et al.Port space allocation with a time dimension［J］.J Operational Res Soc，2007(58):797－807.

［4］王斌.集装箱堆场基于堆存的滚动式计划堆存方法［J］.系统工程学报，2005，20(5):466－471.

［5］李建忠，丁以中，王斌.集装箱堆场空间动态配置模型［J］.交通运输工程学报，2007，7(3):50－55.

［6］陈庆伟.基于遗传算法的堆场贝位分配优化问题研究［D］.青岛:青岛大学，2007.

［7］陶经辉，汪敏.基于堆存模式的集装箱堆场区段分配［J］.系统工程与理论，2009，29(8):185－192.

［8］白治江，王晓峰.基于负载平衡的堆存空间分配优化方案［J］.上海海事大学学报，2008，29(3):60－64.

［9］白治江.动态负载下堆场资源规划的在线决策［J］.上海海事大学学报，2010，31(3):52－57.

［10］严伟，谢尘，苌道方.基于并行遗传算法的集装箱码头堆场分配策略［J］.上海海事大学学报，2009，30(2):14－19.

［11］GEN M，CHENG R，LIN L.Network models and optimization:multi－objective genetic algorithm approach［M］.London:Springer，2008.